Оценка погрешностей интерполяционных формул Ньютона
Интерполяционные формулы Ньютона. Оценка погрешностей первой и второй формулы Ньютона
Первая интерполяционная формула Ньютона
Описание задачи.Пусть для функции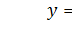 
заданы значения 
для равноотстоящих значений независимой переменной: 
, 
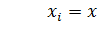, где h–шаг интерполяции. Требуется подобрать полином 
степени не выше n, принимающий в точках 
значения
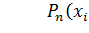, (1)
Условия (1) эквивалентны тому, что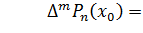 
при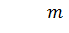 
Интерполяционный полином Ньютонаимеет вид:
(2)
Легко увидеть, что полином (2) полностью удовлетворяет требованиям поставленной задачи. Действительно, во-первых, степень полинома не выше n, во-вторых,
и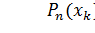 
, 
Заметим, чтопри 
формула (2) превращается в ряд Тейлора для функции 
:
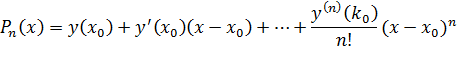
Для практического использования интерполяционную формулу Ньютона (2) обычно записывают в несколько преобразованном виде. Для этого введём новую переменную q по формуле 
, тогда получим:
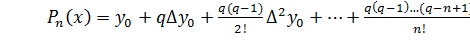, (3)
где 
представляет собойчисло шагов, необходимых для достижения точки , исходя из точки 
. Это и есть окончательный видинтерполяционной формулы Ньютона.Формулу (3) выгодно использовать для интерполирования функции 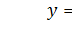в окрестности начального значения 
,где мало по абсолютной величине. Если дана неограниченная таблица значений функции , то число в интерполяционной формуле (3) может быть любым. Практически в этом случае число выбирают так, чтобы разность 
была постоянной с заданной степенью точности. За начальное значение можно принимать любое табличное значение аргумента . Если таблица значений функции конечна, то число ограничено, а именно: не может быть больше числа значенийфункции , уменьшенного на единицу.
|
|
|
Вторая интерполяционная формула Ньютона
Описание задачи. Пусть имеем последовательность значений функции
, для равноотстоящих значений аргумента 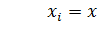, где - шаг интерполяции. Построим полином следующего вида:
,
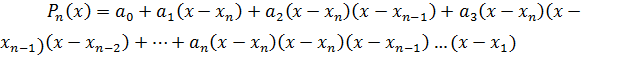или, используя обобщённую степень, получаем:
(4)
Тогда, при выполнении равенства ,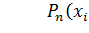 
, получим
,
Подставим эти значения в формулу (1). Тогда, окончательно, вторая интерполяционная формула Ньютона имеет вид:
. (5)
Введём более удобную запись формулы (2). Пусть 
, тогда
, 
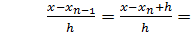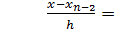, и. т. д.
Подставив эти значения в формулу (2), получим:
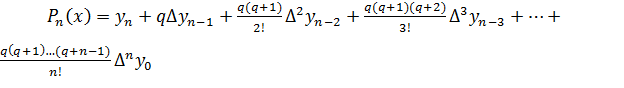(3)
Это и есть обычный вид второй интерполяционной формулы Ньютона. Для приближённого вычисления значений функции полагают: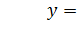 
Как первая, так и вторая интерполяционные формулы Ньютона могут быть использованы для экстраполирования функции, т. е. для нахождения значений функции для значений аргументов , лежащих вне пределов таблицы . Если 
и близко к , то выгодно применять первую интерполяционную формулу Ньютона, причём тогда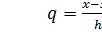 
. Если же и близко к , то удобнее пользоваться второй интерполяционной формулой Ньютона, причём 
. Таким образом, первая интерполяционная формула Ньютона обычно используется для интерполирования вперёд и экстраполирования назад, а вторая интерполяционная формула Ньютона, наоборот, - для интерполирования назад и экстраполирования вперёд.
|
|
|
Оценка погрешностей интерполяционных формул Ньютона
Для интерполяционных формул Ньютона оценки погрешности приобретают следующий вид:
1-я формула Ньютона:
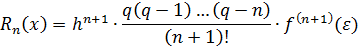
2-я формула Ньютона:
При использовании интерполяционных формул Ньютона величину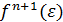 
можно приближенно оценивать по величинам конечных разностей:
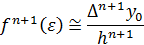
И в этом случае формулы для оценки погрешности приобретают следующий вид:
1-я формула Ньютона:
2-я формула Ньютона:
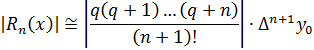
Сравнивая эти формулы с формулами Ньютона, можно увидеть, что для оценки погрешности при интерполяции многочленом n–й степени надо взять дополнительный узел и вычислить слагаемое (n+1) –й степени. Если задана допустимая погрешность интерполяции ε, то надо последовательно добавлять новые узлы и, соответственно, новые слагаемые, увеличивая степень интерполяционного многочлена до тех пор, пока очередное слагаемое не станет меньше ε.
|
|
|
Дата добавления: 2018-02-28; просмотров: 2715; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!