Способы задания движения точки

• Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
• В векторной системе положение точки относительно начала отсчета задается радиус-вектором.
  Закон движения: .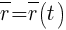
• В системе координат OXYZ положение точки задается тремя координатами X, Y, Z.
  Закон движения: x = x(t), y = y(t); z = z(t).
• В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории.
  Закон движения: .
  Движение точки, при естественном способе задания движения, определено если известны:
  1) Траектория движения.
  2) Начало и направление отсчета дуговой координаты.
  3) Уравнение движения.
  При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:
  Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.
  Главная нормаль (n) – направлена в сторону вогнутости кривой.
  Бинормаль (b) – направлена перпендикулярно к осям τ, n.

Определение кинематических характеристик точки

• Траектория точки
  В векторной системе отсчета траектория описывается выражением: .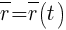
  В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f(x,y)— в пространстве, или y = f(x) – в плоскости.
  В естественной системе отсчета траектория задается заранее.
• Определение скорости точки в векторной системе координат
  При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени: .
  Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости): .
  Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки.
  Вывод: скорость точки – векторная величина, равная производной от закона движения по времени.
  Свойство производной: производная от какой либо величины по времени определяет скорость изменения этой величины.
• Определение скорости точки в координатной системе отсчета
  Скорости изменения координат точки:
  .
  Модуль полной скорости точки при прямоугольной системе координат будет равен:
  .
  Направление вектора скорости определяется косинусами направляющих углов:
  ,
  где — углы между вектором скорости и осями координат.
• Определение скорости точки в естественной системе отсчета
  Скорость точки в естественной системе отсчета определяется как производная от закона движения точки: .
  Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях определяется только одной проекцией .

Ускорение точки

• По определению ускорение характеризует изменение скорости, то есть скорость изменения скорости.
• Ускорения точки в векторной системе отсчета
  На основании свойства производной:
  .
  Вектор скорости может изменяться по модулю и направлению.
  Вектор ускорения направлен по линии приращения вектора скорости, т. е. в сторону искривления траектории.
• Ускорение точки в координатной системе отсчета
  Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат:
  .
  Полное ускорение в прямоугольной системе координат будет определяться выражением:
  .
  Направляющие косинусы вектора ускорения:
  .
• Ускорение точки в естественной системе отсчетаПриращение вектора скорости можно разложить на составляющие, параллельные осям естественной системы координат:
  .
  Разделив левую и правую части равенства на dt, получим:
  ,
  где — тангенциальное ускорение;
  — нормальное ускорение;
  R — радиус кривизны траектории в окрестности точки.

Кинематика твердого тела

• В кинематике твердых тел решаются две основные задачи:
  1) задание движения и определение кинематических характеристик тела в целом;
  2) определение кинематических характеристик точек тела.
• Поступательное движение твердого тела
  Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
  Теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
  Вывод: поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.
• Вращательное движение твердого тела вокруг неподвижной оси
  Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
  Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
  Закон вращательного движения тела вокруг неподвижной оси .
  Угловую скорость и угловое ускорение тела определим методом дифференцирования:
  — угловая скорость, рад/с;
  — угловое ускорение, рад/с².
  Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .
  Модуль линейной скорости:
  .
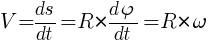  Ускорение точки М при известной траектории определяется по его составляющим :
  ,
  где .
  В итоге, получаем формулы
  тангенциальное ускорение: ;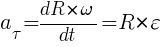
  нормальное ускорение: .

---

Дата добавления: 2018-02-28; просмотров: 308; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!