Преобразование сходящейся системы сил
- Равнодействующая
двух сходящихся сил находится на основании аксиомы о параллелограмме сил.
Геометрическая сумма любого числа сходящихся сил может быть определена путем последовательного сложения двух сил – способ векторного многоугольника.
Вывод: система сходящихся сил (
) приводится к одной равнодействующей силе . - Аналитически равнодействующая сила может быть определена через ее проекции на оси координат:
Согласно теореме: проекция равнодействующей на ось равна сумме проекций слагаемых сил на эту ось:
, или в общем виде 
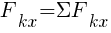
С учетом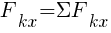 равнодействующая определяется выражением:
. - Направление вектора равнодействующей определяется косинусами углов между вектором и осями x, y, z:
Преобразование произвольной системы сил
- Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится.
В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов — суммарным моментом.
Суммарный вектор — это главный вектор системы сил.
Суммарный момент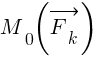
— это главный момент системы сил.
Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору и главному моменту системы сил. - Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат:
,
Условия равновесия систем сил
|
|
|
- Равновесие системы сходящихся сил
Действие системы сходящихся сил эквивалентно действию одной равнодействующей силы.
Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю
.
Из формулы следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю:
- Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю:
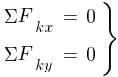
Равновесие произвольной системы сил.
- Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия:
. - Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю:
- Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю:
Кинематика
|
|
|
Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.
Основные понятия кинематики
Дата добавления: 2018-02-28; просмотров: 436; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!