Интегральный признак Коши сходимости рядов
Пусть дан положительный ряд 
. Общий член ряда 
. Восстановим в общем члене исходный аргумент х и вычислим несобственный интеграл 
. Пределы в интеграле соответствуют начальному и конечному значению nв сумме ряда. Тогда можно утверждать, что ряд и интеграл сходятся и расходятся одновременно, т.е. оба выражения одновременно или равны числу или равны 
или вообще не существуют. Теорему можно пояснить на чертеже. дает площадь криволинейной трапеции, ограниченной графиком функции. Ряд это площадь ступенчатой фигуры, каждый прямоугольник которой имеет ширину равную 1 и высоту
. Признак сходимости Коши утверждает, что или обе площади конечны, или обе бесконечны.
Рис. 15.1. Признак Коши сходимости рядов.
Признак Коша позволяет доказать сходимость или расходимость обобщенного гармонического ряда 
Заменим 
. Вычислим интеграл от 
В зависимости от величины pполучим три разных ответа
, так как 
. Ряд расходится.
. В ответе число. Ряд сходится (напомним, что 
)
.
Ряд сходится только при 
.
Знакочередующиеся ряды
Знакочередующимися рядами называются ряды вида
(15.17)
где все un> 0.
Сходимость таких рядов исследуется по теоремеЛейбница: если в знакочередующемся ряде гдеun> 0
Члены ряда удовлетворяют двум условиям
а. члены убывают u1 >u2 >u3 >u4 ... 
.. .
|
|
|
б. 
, т. е. выполнен необходимый признак сходимости ряда,
то ряд ( 15.17) сходится, его сумма положительна и не превосходит первого члена ряда u1.
Доказательство. Возьмем сумму четного числа первых членов S2m, которая по первому условию положительнаS2m = (u1 - u2) + (u3 - u4 ) + ... ...+ ( u2m-1 – u2m ) > 0, так как выражение в каждой скобке больше нуля. S2m возрастает при росте m, т.к.S2m =S2(m-1)+ +(u2m-1 – u2m) >S2(m-1)по тому же первому условию.
С другой стороны S2m = u1 - (u2 - u3)- (u4 – u5)... ...- ( u2m-2 - u2m-1) – u2m<u1 , т. е. при росте mS2m возрастает и ограничена сверху. Следовательно, существует предел четных суммS =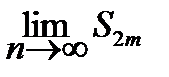 
. Проверим, что нечетные суммы будут иметь тот же предел S2m+1 = =S2m+ u2m+1. 
+ 
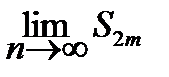=S + 0 = S.
Четные и нечетные суммы ряда имеют тот же предел, следовательно, ряд сходится. Теорема доказана.
По знакочередующемуся ряду можно построить соответствующий ему положительный ряд u1 + u2+ u3 + ... + un + ... = 
. Если такой положительный ряд сходится, то знакочередующийся ряд называют абсолютно сходящимся, в противном случае ряд называют условно сходящимся. В абсолютно сходящемся ряде члены ряда можно переставлять без потери сходимости, в условно сходящемся ряде перестановка членов ряда запрещена, т.к. она может привести к потере сходимости.
|
|
|
Дата добавления: 2018-02-28; просмотров: 279; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!