Признаки сходимости числовых рядов c положительными членами

Учебный модуль 7.Последовательности и ряды. Тема 15. Числовые ряды.

 

ЛЕКЦИЯ 15. Числовые ряды. Признаки сходимости числовых рядов.

 

Пусть дана функция . Если областью определения функции является множество натуральных чисел , то мы говорим, что значения функции образуют бесконечную числовую последовательность

 

.

 

называется общим членом последовательности. Для сокращения записи вводится обозначение . Тогда последовательность можно записать так

 

u₁, u₂, u₃, ...,u_n…                                                                                                 (15.1)

 

Замечание. Областью определения функция может быть и множество натуральных чисел с добавлением нуля .

Пусть задана бесконечная числовая последовательность чисел (15.1). Числовым рядом называется последовательность чисел, члены которой соединены знаком плюс, т.е. выражение

u₁ + u₂+ u₃ + ... + u_n + ... = .                                                             (15.2)

числа u₁, u₂, u₃, ..., u_n, ... называются членами ряда, а u_n общим членом ряда.

Например, числовой ряд

имеет общий член u_n=

Сходимость и сумма ряда. Частичной суммой S_nназывается сумма первых n членов ряда, т.е.

 

 

Частичные суммы ряда образуют новую последовательность - последовательность частичных суммS₁, S₂, S₃, ..., S_n, .... Если существует конечный предел последовательности частичных сумм 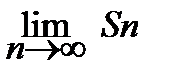= S<¥, то ряд (15.2) называется сходящимся, а число S - суммой ряда. В этом случае пишут . Если такой предел не существует или равен бесконечности, то ряд называют расходящимся.

Разность между рядом и его частичной суммой называется остатком ряда и обозначается .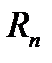

или

Пример 1. Определить сходимость ряда

Решение.Напишем частичную сумму заданного ряда

Каждое из слагаемых представим в виде суммы простейших так, как это делали в интегралах

 

Числители выражений слева и справа равны, подставляя в равенство корни знаменателя, найдемА и В

то есть

.

Применим формулу к каждому члену частичной суммы ряда

Рассмотрим предел частичных сумм

 

Следовательно, ряд сходится и его сумма равна 1.

Пример 2. Дан числовой ряд

исследовать сходимость ряда.

Решение.Члены ряда положительны. Заменим в частичной сумме каждое слагаемое на последнее 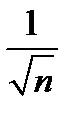, тем самым уменьшим частичную сумму

Величина 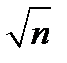 бесконечно возрастает с ростом n. Поэтому предел последовательности S_nпри n®¥ равен бесконечности и ряд расходится.

Пример3. Определить сходимость следующего ряда:

1 - 1 + 1 - 1 + (-1)ⁿ⁺¹ + ... .

Решение. Четная частичная сумма этого ряда S_2n= 0, а нечетная - S_2n+1 = 1. Это означает, что предел не существует. Следовательно, данный ряд расходится.

 

Теорема о необходимом условии (признаке) сходимости числового ряда. Если числовой ряд сходится, то его общий член при n ®¥ стремится к нулю, т.е.

 

                                                                                                   (15.3)

 

Доказательство. Рассмотрим две соседние частичные суммы ряда (15.2)

S_n-1 = u₁+ u₂+ u₃ + ... u_n-1,

S_n=u₁+ u₂+ u₃+ ... u_n-1 + u_n=S_n-1 +u_n.

Из сходимости ряда следует, что

С другой стороны, по теоремам о пределах,

т.е.

S = S +

откуда и следует (15.2) .

Введенное условие сходимости является лишь необходимым, но не достаточным. Это означает, что существуют расходящиеся ряды, у которых .

Пример. Ряд, рассмотренный в примере 2

Расходится, но его общий член стремится к нулю. Действительно

Аналогичным свойством обладает гармонический ряд, который будет рассмотрен ниже.

 

Основные свойства сходящихся числовых рядов.

Свойство 1. Ряд и его остаток сходятся и расходятся одновременно. Действительно, частичная сумма ряда при фиксированномnесть число. Рассмотрим сумму mслагаемых .

.

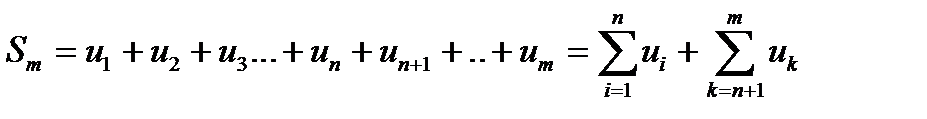Рассмотрим предел этого выражения при . Так как предел постоянной равен самой постоянной, а 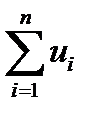от m не зависит и является величиной постоянной, то

.

Оба предела одновременно конечны или бесконечны.

Следствие. Добавление или отбрасывание конечного числа членов не изменяет сходимости ряда.

Свойство 2. При умножении ряда на число с его сходимость не меняется. Докажем свойство для сходящихся рядов. Если ряд

u₁ + u₂+ u₃ + ... + u_n + ... = .                                                                 

сходится и имеет сумму S, то ряд

 

cu₁  + cu₂  + ... + cu_n+ ..,                   

 

также сходится и имеет сумму с∙S.

Доказательство. Рассмотрим частичную сумму ряда

 

s_n=cu₁  + cu₂ + cu₃ + ... + cu_n= cS_n.

 

Поэтому

 

 

Свойство 3. Сходящиеся ряды можно почленно складывать и вычитать.

Доказательство. Пусть

u₁+ u₂  + u₃ + ... + u_n + ... = S;

v₁+ v₂+ v₃ + ... + v_n + ... = Ф,

тогда ряд

(u₁±v₁) + (u₂ ±v₂) + ... + (u_n±v_n) + ...

также сходится и имеет сумму S±Ф, так как предел суммы равен сумме пределов

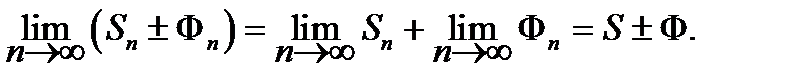
Замечание. При сложении сходящегося и расходящегося ряда суммарный ряд тоже будет расходится.

 

Признаки сходимости числовых рядов c положительными членами

 

Числовой ряд называется рядом с положительными членами или просто положительным рядом, если все члены ряда

 

u₁ + u₂+ u₃ + ... + u_n + ...

 

больше нуля 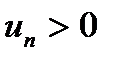. Рассмотрим признаки сходимости для положительных рядов.

Первый признак сравнения. Пусть даны три ряда:

 ряд, сходимость которого надо определить

 

u₁ + u₂+ u₃ + ... + u_n + ...                                                                         (15.4)

 

сходящийся рядv₁+ v₂+ v₃ + ... + v_n + ...                                                   (15.5)

 

расходящийся рядw₁ + w₂  + w₃ + ... + w_n + ...                                         (15.6)                                       

 Тогда:

а) если начиная с некоторого номера n, выполняется условиеu_n£v_n (15.7)

 

то из сходимости ряда (15.5) следует сходимость ряда (15.4);

б) если, начиная с некоторого номера n, выполняется условиеu_n³w_n (15.8)

то из расходимости ряда (15.6) следует расходимость ряда (15.4).

Доказательство.

 а). Обозначим частичные суммы рядов

S_n= u₁+ u₂  +u₃ + ... + u_n

Ф_n= v₁+ v₂+ v₃ + ... + v_n

в силу условия (15.7) имеем S_n£Ф_n.

По условию ряд (15.5) сходится, т.е.  = Ф, следовательно

Ф³Ф_n³S_n.

Это означает, что последовательность частичных сумм S_n возрастает (в силу положительности ряда (15.4)) и ограниченна сверху величиной Ф. Поэтому  существует и конечен, а ряд (15.4) сходится.

б). Обозначив частичную сумму ряда (15.6) за W_n

W_n = w₁ + w₂ + w₃ + ... + w_n,

в силу (15.8) имеем S_n³W_n.

По условию ряд (15.6) расходится, т.е. = ¥, следовательно

и ряд (15.4) расходится.

 

Второй признак сравнения. Пусть даны два ряда

 

u₁ + u₂+ u₃ + ... + u_n + ...                                                                        (15.9)

v₁+ v₂+ v₃ + ... + v_n + ...                                                                         (15.10)

 

и можно указать такие постоянные числа k₁> 0 и k₂> 0, что, начиная с некоторого достаточно большого n,

 

                                                                                               (15.11)

Тогда ряды (15.9) и (15.10) одновременно сходятся или одновременно расходятся.

Доказательство. Из (15.11) следует, что

 

k₁v_n£u_n£k₂ v_n.                                                                                        (15.12)

 

Если ряд (15.9) сходится, то из левого неравенства (15.12) по первому признаку сравнения вытекает сходимость ряда

k₁ v₁ + k₁v₂  +k₁v₃ + ... + k₁v_n + ...

Из сходимости этого ряда,по свойству 2, вытекает и сходимость ряда (15.10).

Предположим теперь, что ряд (15.9) расходится. В этом случае расходится и ряд

Из правой части (15.11) следует, что

Следовательно, по первому признаку сравнения, ряд (15.10) также расходится.

Следствие (предельный признак сравнения). Если для рядов (15.9) и (15.10) выполняется условие

 = r<¥, где r ¹ 0,                                                                         (15.13)

то эти ряды сходятся или расходятся одновременно.

 

Для сравнения обычно используются следующие эталонные ряды.

Геометрический ряд (ряд геометрической прогрессии)

a + aq + aq² + ... + aq^n-1 + ... .

Геометрический ряд сходится при условии . В противоположном случае ( ³ 1) ряд расходится. Например, ряд

сходится ( ), а ряд

1 + 2 + 4 + ... + 2^n-1 + ...

расходится (q = 2). Можно также сказать, что этот ряд расходится потому, что не выполнено необходимое условие сходимости ряда.

Обобщенным гармоническим рядом называется ряд

Этот ряд сходится при p> 1 и расходится при p£ 1.

Например, ряд

- сходится, а ряд

- расходится.

Обобщенный гармонический ряд при p = 1 называют просто гармоническим рядом:

Гармонический ряд расходится!

Действительно, сгруппируем члены ряда по степеням 2

так как сумма слагаемых в каждой скобке больше , то

Пример. Исследовать сходимость ряда

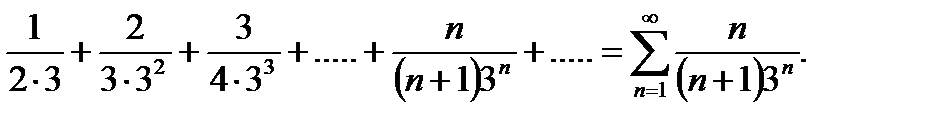
Решение. Сравним общий член этого ряда с геометрическим рядом , который сходится.

Так как

то, по первому признаку сравнения исследуемый ряд сходится.

Пример. Исследовать сходимость ряда

Решение. Сравнивая общий член этого ряда с общим членом гармонического ряда

заключаем, что этот ряд также расходится (по первому признаку сравнения).

Пример. Исследовать сходимость ряда

Решение. Воспользуемся следствием из второго признака сравнения, сравним с расходящимся гармоническим рядом

При вычислении предела мы использовали правило Лопиталя: предел отношения двух функций с неопределенностью или  равен пределу отношения производных . Поэтому .

Сравниваемые ряды ведут себя одинаково, поэтому заключаем, что исследуемый ряд расходится (т.к. гармонический ряд расходится).

Пример. Исследовать сходимость ряда

Решение. Рассмотрим отношение членов этого ряда к соответствующим членам гармонического ряда:

- при нечетном n имеем

- при четном n имеем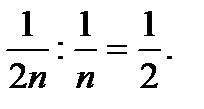    

Следовательно, отношениеu_n/v_n ни к какому пределу не стремится. Однако при всех n оно заключено между 1/2 и 2. Поэтому согласно второму признаку сравнения исследуемый ряд ведет себя так же, как и гармонический, т.е. расходится.

 

Признак Даламбера сходимости рядов. Пусть дан положительный ряд

u₁ + u₂+ u₃ + ... + u_n + ...                                                                           (15.14)

Если отношения последующего члена ряда u_nк предыдущему u_n-1, начиная с некоторого значения n = N , удовлетворяет неравенству

                                                                                     (15.15)

то ряд (15.14) сходится.

Если же, начиная с некоторого N , имеем

                                                                                          (15.16)

то ряд (15.14) расходится.

Доказательство. Пусть соотношение (15.14) выполняется для всех n. По первому свойству рядов без потери сходимости можно отбросить конечное число первых членов ряда. Тогда

u_n£q u_n-1, u_n-1 £q u_n-2, ... , u₂ £q u₁.

Отсюда, подводя почленную подстановку, и возвращаясь к u_nполучим

u_n£u₁q^n-1                                                                                                                                                      

Это неравенство означает, что общий член ряда (15.14) не превосходит соответствующего члена сходящегося (q< 1) геометрического ряда. В силу первого признака сравнения ряд (15.14) сходится.

Пусть имеет место соотношение (15.16). Тогда

u₁ <u₂ <u₃ < ...<u_n-1 <u_n<... ,

т.е. члены ряда не убывают по мере возрастания n. Следовательно, не выполнено необходимое условие сходимости ряда и ряд (15.14) расходится.

На практике удобнее пользоваться предельным признаком Даламбера, формулировку которого дадим в виде следствия.

Следствие. (Предельный признак Даламбера). Если

,

то при p< 1 ряд (15.14) сходится, при p> 1 этот ряд расходится.

Пример. Исследовать сходимость ряда

Решение. Рассмотрим предел отношения

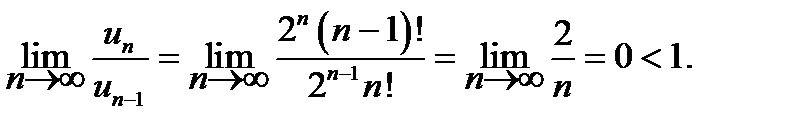
Следовательно, исследуемый ряд сходится.

Замечание. Если  , то признак Даламбера не дает ответа на вопрос о сходимости ряда. В этих случаях надо привлекать другие признаки сходимости ряда.

Признак Даламбера хорошо работает для рядов, содержащих  и .

---

Дата добавления: 2018-02-28; просмотров: 437; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!