РОЗДІЛ 1. ЗАГАЛЬНІ ВІДОМОСТІ ПРО МЕТОДИ МАТЕМАТИЧНОЇ СТАТИСТИКИ, ЯКІ ВИКОРИСТОВУЮТЬСЯ У ФІЗИЧНОМУ ВИХОВАННІ І СПОРТІ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«ЗАПОРІЗЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ»
МІНІСТЕРСТВА ОСВІТИ І НАУКИ УКРАЇНИ
О.В. Соколова, Г.А. Омельяненко
МЕТОДИ МАТЕМАТИЧНОЇ СТАТИСТИКИ
У ФІЗИЧНОМУ ВИХОВАННІ
(з використанням електронних таблиць)
Навчально-методичний посібник для студентів
освітньо-кваліфікаційного рівня “бакалавр”
Напрямів підготовки “Фізичне виховання”,
“Спорт”, “Здоров’я людини”
Запоріжжя
2014
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«ЗАПОРІЗЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ»
МІНІСТЕРСТВА ОСВІТИ І НАУКИ УКРАЇНИ
О.В. Соколова, Г.А. Омельяненко
МЕТОДИ МАТЕМАТИЧНОЇ СТАТИСТИКИ
У ФІЗИЧНОМУ ВИХОВАННІ
(з використанням електронних таблиць)
Навчально-методичний посібник для студентів
освітньо-кваліфікаційного рівня “бакалавр”
напрямів підготовки “Фізичне виховання”,
“Спорт”, “Здоров’я людини”
Затверджено
вченою радою ЗНУ
Протокол № від
Запоріжжя
2014
УДК: 37.037.1:519.2(075)
ББК: Ч411.354 я73
С 594
Соколова О.В., Омельяненко Г.А. Методи математичної статистики у фізичному вихованні (з використанням електронних таблиць): навчально-методичний посібник для студентів освітньо-кваліфікаційного рівня “бакалавр” напрямів підготовки “Фізичне виховання”, “Спорт”, “Здоров’я людини”. – Запоріжжя: ЗНУ, 2014. – 94 с.
|
|
|
У навчально-методичному посібнику подано загальні відомості про методи математичної статистики, які використовуються у фізичному вихованні і спорті, наведено короткий опис електронних таблиць Excel, що дозволить майбутнім фахівцям з фізичного виховання і спорту сформувати комплексне уявлення про методи математичної статистики та їх практичне застосування. Практичні заняття систематизовані відповідно до методів математичної статистики, запропонованих для вивчення. Також пропонується алгоритм вирішення конкретного прикладу з виду спорту, в тому числі і за допомогою засобів Excel. Для діагностики рівня засвоєння знань наведено питання для самоконтролю. Поглибленню знань сприятиме рекомендована література. Виконання практичних завдань за наданим алгоритмом з використанням редактора електронних таблиць Excel допоможе студентам глибше засвоїти теоретичний матеріал і в майбутньому використовувати його у своїй практичній діяльності.
Навчально-методичний посібник розрахований на студентів факультету фізичного виховання денної та заочної форм навчання.
Рецензент М.В. Маліков
|
|
|
Відповідальний за випуск А.П. Конох
ЗМІСТ
Передмова……………………………………………………….................................6
Розділ 1. Загальні відомості про методи математичної статистики,
які використовуються у фізичному вихованні і спорті………….……….….9
1.1 Метод середніх величин.Правильність добору групи досліджуваних. Середнє арифметичне значення. Медіана. Мода. Визначення однорідності і однотипності групи. Середнє квадратичне відхилення. Помилка середнього арифметичного. Коефіцієнт варіації.…………………………………………………………………..…….11
1.2 Вибірковий метод.Порівняння двох середніх арифметичних за допомогою критерію Стьюдента. Достовірність різниць. Причини достовірності різниць. Ефективність тренувального процесу, переважність методик, підготовленість. Порівняння двох вибіркових характеристик варіації за критерієм Фішера. Модельні характеристики………………………………………………..…………...….15
1.3 Кореляційний аналіз. Визначення залежності між двома вимірюваними показниками. Коефіцієнт кореляції. Взаємозв’язок між двома вимірюваними величинами, форма та спрямованість взаємозв’язку. Кореляційне поле. Знаходження найбільш імовірних лінійних залежностей між двома факторами (побудова прямих регресій).……………………………………………………………………….20
|
|
|
1.4 Ряди динаміки. Відображення у часі явища, що підлягає дослідженню; його оцінка й прогнозування за допомогою рядів динаміки. Статистична крива. Основні характеристики рядів динаміки. Абсолютний приріст, темп росту, темп приросту. Аналіз і прогноз явища…………………………………………………………………………..25
1.5 Дисперсійний аналіз. Вивчення впливу факторної ознаки, залежно від її градацій, на результативну ознаку в практиці спортивної діяльності. Оцінка тренувальних впливів. Вплив умов спортивної діяльності………..28
Питання для самоконтролю……………………………………………………….31
Розділ 2. Короткий опис електронних таблиць Excel……………………………33
Розділ 3. Практичні заняття………………………………………………………..45
Практичне заняття № 1
Метод середніх величин. Визначення правильності добору
групи, яка підлягає дослідженню……………………………………….……45
Практичне заняття № 2
Метод середніх величин. Визначення однорідності та
однотипності групи, яка підлягає дослідженню ……………..……………..56
Практичне заняття № 3
Вибірковий метод. Порівняння двох вибіркових середніх
арифметичних за допомогою критерію Стьюдента …………..………..…..66
|
|
|
Практичне заняття № 4
Вибірковий метод. Визначення середньостатистичних
показників генеральної сукупності (модельних
характеристик)…………………………………….……………………...….74
Практичне заняття № 5
Вибірковий метод. Порівняння двох вибіркових
характеристик варіації за критерієм Фішера……………………………....78
Практичне заняття № 6
Кореляційний аналіз.Оцінка залежності між двома
величинами, що вимірюються ………………………………………………82
Література………………………………………………………………………..…91
Додаток А. Таблиця граничних значень критерію Стьюднта……………….....93
Додаток В. Таблиця граничних значень критерію Фішера F………………..….94
ПЕРЕДМОВА
Сучасний розвиток суспільства поставив нові завдання і вимоги до педагогічних кадрів, які працюють у галузі фізичного виховання, фізичної реабілітації та спорту. Працівники цієї сфери повинні не тільки навчити людину керувати своїми рухами й тілом, а ще й здійснювати якісно-кількісний аналіз рухової діяльності. Тобто навчити обробляти й аналізувати статистичний матеріал, який ми отримуємо в результаті проведення експериментальних досліджень у фізичному вихованні та спорті.
Виділяють три основні етапи статистичних досліджень.
1. Статистичне спостереження – планомірний, науково обґрунтований збір даних, що характеризують даний об’єкт. Воно повинно задовольняти наступні вимоги:
а) об’єкти спостереження повинні бути однорідними з точки зору їхніх властивостей (стать, вік, професія, національність, умови харчування, спортивна спеціалізація і кваліфікація, місця проживання та ін.) і умов виміру (час доби, діяльність, що передує вимірам, температура повітря, особистість експериментатора, освітленість та ін.). У вимірах на живих об’єктах максимально можлива стандартизація може бути досягнута тільки в експериментах з лабораторними тваринами;
б) виміри повинні проводитися за допомогою об’єктивних методик (властивості яких також підтверджуються статистичними методами) в однакових шкалах виміру;
в) кількість об’єктів спостереження має бути достатньою, щоб можна було виявити закономірності й узагальнити їхні властивості.
2. Статистичне зведення та групування є підготовчою частиною до статистичного аналізу даних. Цей етап передбачає:
а) систематизацію (групування) даних;
б) оформлення певних статистичних таблиць.
3. Аналіз статистичного матеріалу передбачає використання відповідних математико-статистичних методів, створення статистичних графіків і діаграм за їх результатами.
Є велика кількість статистичних методів. У практиці фізичного виховання та спорту найбільш часто застосовуються наступні:
а) описові статистики досліджуваної вибірки (метод середніх величин);
б) визначення взаємозв’язків між досліджуваними явищами (кореляційний аналіз);
в) визначення вірогідності різниць між вибірками і взаємозв’язками (вибірковий метод);
г) аналіз і прогнозування часових рядів (метод індексів, або ряди динаміки);
д) вивчення впливу факторної ознаки, залежно від її градацій, на результативну ознаку (дисперсійний аналіз).
Оволодіння методами математичної статистики дозволить максимально ефективно використовувати та проводити математичну обробку та аналіз експериментальних даних. У системі підготовки фахівців з фізичної культури навчальна дисципліна “Методи математичної статистики у фізичному вихованні” займає важливе місце.
Предметом вивчення навчальної дисципліни є методи математичної статистики, що застосовуються у фізичному вихованні і спорті у процесі систематизації, обробки й аналізу результатів дослідження.
Навчальна дисципліна “Методи математичної статистики у фізичному вихованні” пов’язана з циклом дисциплін математичної та природничо-наукової підготовки, які мають забезпечити студентів відповідними знаннями і сформувати вміння застосовувати їх у майбутній професійній діяльності, а саме: статистикою, теорією ймовірностей, спортивною метрологією, інформатикою, комп’ютерною технікою, теорією та методикою фізичного виховання, анатомією, біологією, фізіологією людини, фізіологією спорту тощо.
Дисципліна охоплює всі питання, необхідні для аналізу результатів тренувань, спортивних змагань, контрольних іспитів, підбору вправ для підвищення загальної та спеціальної фізичної підготовленості спортсменів, підтвердження висновків, зроблених шляхом математичних розрахунків на основі спостережень із застосуванням сучасних інформаційних технологій.
Метою викладання навчальної дисципліни “Методи математичної статистики у фізичному вихованні” є забезпечення глибокої теоретичної та практичної підготовки майбутніх фахівців з фізичного виховання, формування базових знань з основ математичної статистики, ознайомлення з основними методами кількісної оцінки, що застосовуються у спортивній практиці при обробці результатів дослідження та їх практичним застосуванням.
Основними завданнями вивчення дисципліни “Методи математичної статистики у фізичному вихованні” є забезпечити підвищення рівня педагогічної компетентності студентів. Навчити методам математичної статистики, що застосовуються у спортивній галузі. Сформувати у студентів вміння правильно підбирати метод математичної статистики при вирішенні конкретного завдання з виду спорту. Навчити розраховувати основні параметри варіаційного ряду та критерії достовірності математичної статистики. Навчити майбутнього вчителя фізичної культури, тренера аналізувати результати досліджень на основі використання методів математичної статистики.
Згідно з вимогами освітньо-професійної програми студенти повинні:
знати:
основні поняття та положення курсу;
методи математичної статистики, що застосовуються у спортивних дослідженнях;
особливості застосування методів математичної статистики залежно від умов виконання певних задач з виду спорту;
які висновки необхідно зробити після обробки результатів дослідження методами математичної статистики.
вміти:
розраховувати основні характеристики та параметри варіаційного ряду, критерії нормального розподілу, коефіцієнт кореляції, коефіцієнт детермінації;
робити висновки щодо підбору групи, її однорідності; ефективності побудови тренувального процесу; підготовленості спортсменів;
робити порівнювання середніх арифметичних за допомогою критерію Стьюдента;
визначати залежність між двох вимірюваних показників;
визначати вплив факторної ознаки на результативну ознаку в практиці спортивної діяльності.
РОЗДІЛ 1. ЗАГАЛЬНІ ВІДОМОСТІ ПРО МЕТОДИ МАТЕМАТИЧНОЇ СТАТИСТИКИ, ЯКІ ВИКОРИСТОВУЮТЬСЯ У ФІЗИЧНОМУ ВИХОВАННІ І СПОРТІ
Математична статистика – розділ математики, присвячений методам збору, аналізу і обробки статистичних даних для наукових і практичних цілей, оперує великим числом об’єктів і аналізує масові явища.
Будь-який творчо працюючий фахівець фізичного виховання, будь то студент факультету фізичного виховання, який пише курсову або дипломну роботу, аспірант, докторант, науковий співробітник, що аналізує наукові дані, вчитель фізичної культури, тренер, в ході своєї роботи отримують фактичний експериментальний матеріал (первинний цифровий масив). Якщо ці дані не будуть коректно оброблені за допомогою методів математичної статистики, то їх робота втрачає будь-який теоретичний і практичний сенс.
Для побудови логічної розповіді в значенні математичної статистики і питаннях, які вона вирішує в області фізичної культури і спорту, введемо деякі визначення.
Генеральна сукупність – початкова сукупність (абсолютна кількість об’єктів, яка існує в наявності взагалі, наприклад, всі студенти Запорізького національного університету 2014 р.).
Вибірка – частина об’єктів дослідження, певним чином вибрана з генеральної сукупності (наприклад, студенти факультету фізичного виховання ЗНУ 2014 р. – це об’єкти дослідження, вибрані з генеральної сукупності за ознакою приналежності до факультету).
Всі об’єкти дослідження повинні мати хоча б одну загальну ознаку, що дозволяє класифікувати об’єкти, порівнювати їх один з одним (стать, вік, спортивна кваліфікація і т. п.). В цьому випадку про ці об’єкти можна говорити як про статистичну сукупність.
Фактичний експериментальний матеріал з’являється в ході наукового експерименту. Його традиційна схема наступна: зазвичай особи, які беруть участь у наукових дослідженнях, діляться на контрольну і експериментальну групи, в яких важливе значення мають ознаки, що визначають досліджуваних як статистичну сукупність. Ці ознаки мають бути приблизно однаковими за своїми характеристиками. Інакше сенс експерименту втрачає свою наукову значущість.
Контрольна група готується за традиційною методикою, а експериментальна – із застосуванням нововведень. До і після експерименту проводяться контрольні випробування (зрізи) і по їх результатах судять про ефективність нововведень.
Вже на етапі відбору в контрольну і експериментальну групи дослідник стикається з рядом питань: яка має бути чисельність групи, як повинні відбиратися кандидати в ці групи, рівень підготовленості учасників експерименту, чи істотно відрізняється одна група від іншої за важливими для експерименту показниками і так далі. На всі ці питання можна відповісти тільки застосувавши методи математичної статистики. Наприклад, існують методи, що дозволяють однозначно сказати про те, що вибірка є представницькою (репрезентативною) по відношенню до генеральної сукупності. До них відносяться:
1) Методи відбору об’єктів з генеральної сукупності у вибірку:жеребкування;механічний відбір;типовий відбір;серійний відбір.
2) Методи точкових і інтервальних оцінок, що дозволяють виявити максимально близькі значення і межі інтервалів, між якими з більшою вірогідністю знаходяться дійсні значення параметрів, які визначаються.
3) Методи, які дозволяють виявити той мінімальний обсяг, який би дозволяв судити про середнє значення генеральної сукупності не більше ніж з помилкою на задану величину після проведення контрольних зрізів.
4) Методи описової статистики:
· групування даних і надання їх у вигляді статистичних таблиць з визначенням в них варіаційних рядів.
· графічне представлення експериментальних даних у вигляді гістограм і полігону частот.
5) Методи, що дають уявлення про кількісні числові характеристики:
· характеристики положення: середнє арифметичне; медіана; мода;
· характеристики розсіяння: дисперсія; стандартне відхилення; коефіцієнт варіації;
· характеристики асиметрії емпіричних розподілів:асиметрія;ексцес.
6) Методи перевірки статистичних гіпотез:
· Критерії, засновані на нормальному розподілі: t- критерій Стьюдента; F - критерій Фішера; U - критерії.
· Критерії згоди: 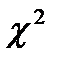 - критерій (критерій хі-квадрат); критерій Шапіро-Уїлки.
- критерій (критерій хі-квадрат); критерій Шапіро-Уїлки.
· Непараметричні критерії:критерій Вілкоксона.
7) Дуже часто метою дослідження є встановлення наявності і ступеня зв’язку між спортивним результатом і певним показником тренованості або фізичного розвитку, між окремими показниками фізичної підготовленості і т.п., подібні завдання вирішуються методами кореляційного і регресивного аналізу.
8) Крім того, в деяких випадках дослідникові цікаво дізнатися ступінь тісноти взаємозв’язку одного показника із двома, трьома, чотирма і більш аргументами, що впливають на цей показник. Наприклад, з області біомеханічної науки: у якій мірі (у відсотковому відношенні та сумарно) впливають на результат стрибка в довжину з розгону: початкова швидкість розгону; швидкість розгону на 3 метри до відштовхування; величина кута постановки поштовхової ноги у відштовхуванні; величина кута згинання в колінному суглобі і швидкість руху махової ноги під час відштовхування, висоти польоту в польотній фазі стрибка і так далі Це приклад із багатьма невідомими. Подібні до цього прикладу рівняння вирішуються за допомогою методів множинної кореляції і регресії. Ще складніші питання вирішують факторний та інші види аналізів.
Метод середніх величин. Правильність добору групи досліджуваних. Середнє арифметичне значення. Медіана. Мода. Визначення однорідності і однотипності групи. Середнє квадратичне відхилення. Помилка середнього арифметичного. Коефіцієнт варіації
Сучасні спортивні дослідження містять великі масиви вимірів. Отримані в ході експериментальної роботи дані представлені у вигляді неврегульованого набору чисел. Для того, щоб по ним можна було робити якісь виводи, необхідна первинна їх обробка - угрупування. Спеціальні статистичні операції дають можливість сконцентрувати початковий кількісний матеріал, і при цьому не втрачається корисна інформація. З погляду математичної процедури, така робота зводиться до формування деяких математичних систем, основні характеристики яких дають уяву про початковий масив чисел.
Найпопулярніший метод, що дозволяє зробити такі операції ‑ метод середніх величин. Початкова кількісна інформація при ранжируванні переходить у варіаційний ряд. Характеристики варіаційного ряду дають уявлення про початковий масив чисел. Концентрація початкового кількісного матеріалу і представлення його декількома параметрами є основою для подальших досліджень, тому що потім робота проводиться не з усім масивом чисел, а тільки з характеристиками варіаційного ряду.
Робота над методом середніх величин передбачає три основних етапи:
1. Утворення варіаційного ряду.
2. Знаходження основних характеристик варіаційного ряду:
· обсяг вибірки (N);
· середнє арифметичне значення ( 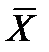 );
);
· медіана (Мех);
· мода (Мох);
· дисперсія (s2);
· середнє квадратичне відхилення (s);
· помилка середнього арифметичного значення (m);
· коефіцієнт варіації (V);
3. Практична реалізація отриманих характеристик.
Метод середніх величин дає можливість визначити середнє значення, припустимі границі досліджуваної вибірки і визначити правильність добору досліджуваної групи, її однорідність і однотипність. Тільки правильно підібрана група, однорідна й однотипна може брати участь у подальших дослідженнях. Якщо група правильно підібрана, то результати дослідження можуть бути використані при подальшій оцінці й аналізі методики тренування, ефективності навчально-виховного процесу і т.п. Прикінцевий результат дослідження можна буде вважати результатом проведення навчально-виховної або навчально-тренувальної роботи, а не наслідком закономірної зміни фізичного розвитку, або фізичної підготовленості.
Для того, щоб скласти варіаційний ряд, необхідно виконати ранжирування варіант.
Ранжирування – операція розташування варіант у порядку зростання або зменшення.
Числа, що входять до складу ранжируваного ряду називаються варіантами, варіанта (Хi)– значення ознаки, що спостерігається.
Кожна варіанта в ранжируваному ряду зустрічається визначену кількість разів – частота варіанти (ni).
Частота варіанти – кількість варіант у ранжируваному ряду.
Вибірка (вибіркова сукупність) ‑ ряд результатів, поданих випадковими числами.
Генеральна сукупність – сукупність усіх значень, які можна було б отримати для досліджуваної вибірки.
Якщо дослідженням охоплена вся генеральна сукупність, то таке дослідження називається суцільним. Такі дослідження мають місце дуже рідко.
Наприклад, якщо комусь вдалося обстежити всіх найсильніших спортсменів світу в якомусь виді спорту, тобто провести суцільне дослідження (тому, що інших найсильніших спортсменів світу в досліджуваному виді спорту на момент обстеження не було), виходить, що обстежено всю генеральну сукупність. Усі наступні дослідження будуть вважатися вибірковими (наприклад, дослідження на рівні України).
Наприклад, довжина тіла студентів одного вузу факультету фізичного виховання (якщо нас цікавлять результати студентів щодо показника, який підлягає дослідженню, тільки одного вузу факультету фізичного виховання) ‑ вибіркова сукупність. А довжина тіла студентів усіх факультетів фізичного виховання України – генеральна сукупність.
Обсяг вибірки (N) – одна з основних характеристик варіаційного ряду, що визначається числом об’єктів спостереження або загальної кількості варіант у ранжируваному ряду, що спостерігається.
Варіаційний ряд – ранжируваний ряд з позначкою частоти або відносної частоти.
Накопичена частота (k) – визначається додаванням попередніх частот.
Накопичена частота першої варіанти в ранжируваному ряду дорівнює її ж частоті, а останньої варіанти – загальній кількості варіант досліджуваного ранжируваного ряду, тобто обсягу вибірки (N).
Медіана (Мех) – основна характеристика варіаційного ряду. Вона визначається як середня варіанта, що розподіляє ранжируваний ряд навпіл.
У залежності від парності або непарності обсягу вибірки, медіана розраховується за формулами:
якщо обсяг вибірки непарний: Мех= X((N+1)/2)
якщо обсяг вибірки парний: Мех= (X (N/2) + X ((N/2) +і))
Мода (Мoх) – основна характеристика варіаційного ряду, вона визначається як варіанта з найбільшою частотою.
Якщо дві варіанти ранжируваного ряду мають однакову найбільшу частоту і розташовуються поруч, то мода – середнє арифметичне значення цих двох варіант; якщо розташовані в різних місцях ранжируваного ряду, то існують дві моди, і вибірка називається бімодальною; якщо всі варіанти зустрічаються однакову кількість разів – моди не існує.
Середнє арифметичне значення( 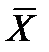 )–основна характеристика варіаційного ряду, що визначається як середній результат досліджуваної вибірки. Середнє арифметичне значення розраховується за формулою:
)–основна характеристика варіаційного ряду, що визначається як середній результат досліджуваної вибірки. Середнє арифметичне значення розраховується за формулою:

Графік залежності варіанти від частоти дає уявлення про нормальний закон розподілу.
Нормальний закон розподілу ‑ закон, при якому переважну більшість варіантів зосереджено в центрі, а по мірі віддалення від центру, кількість їх поступово зменшується, зберігаючи абсолютну симетрію лівого і правого крила нормальної кривої.
Якщо результати вимірів за своїми характеристиками можуть бути віднесені до нормального розподілу, то вибір статистичного методу для аналізу результатів визначений. Це дуже важливо, оскільки для дослідження зменшується ступінь ризику використання неправильного статистичного методу аналізу.
На основі порівняння медіани, моди, середнього арифметичного значення і побудови графіка залежності варіанти від частоти можливо зробити висновок про правильний добір досліджуваної групи.
Якщо результати вимірів за своїми характеристиками можуть бути віднесені до нормального розподілу, то вибір статистичного методу для аналізу результатів визначений. Це дуже важливо, оскільки для дослідження зменшується ступінь ризику використання неправильного статистичного методу аналізу.
На основі порівняння медіани, моди, середнього арифметичного значення і побудови графіка залежності варіанти від частоти можливо зробити висновок про правильний добір досліджуваної групи.
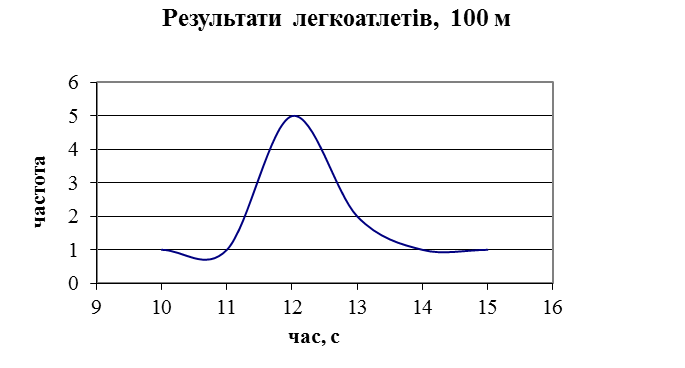
Наприклад: результати легкоатлетів на дистанції 100 м надано у вигляді варіаційного ряду, а 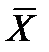 =Мех =Мох =12 (с) (рис. 1):
=Мех =Мох =12 (с) (рис. 1):
Якщо значення медіани, моди і середнього арифметичного значення збігаються, або незначно відрізняються, і графік залежності варіанти від частоти має форму купола, що дозволяє говорити про нормальний закон розподілу, то досліджувану групу можна вважати правильно підібраною відповідно віку, статі, фізичній підготовленості (для осіб, які не займаються спортом), або віку, статі, спеціалізації, кваліфікації (для спортсменів). Така група може брати участь у подальших дослідженнях. Результати дослідження, які були отримані при правильному доборі групи, можна буде використовувати в подальшій роботі.
| Xi, с | nі |
|
| 10 | 1 | |
| 11 | 1 | |
| 12 | 5 | |
| 13 | 2 | |
| 14 | 1 | |
| 15 | 1 |
Рис. 1.Графік залежності варіанти від частоти
Якщо значення медіани, моди і середнього арифметичного значно відрізняються, а графік залежності варіанти від частоти не має форму купола, і має місце лівостороння, або правостороння асиметрія (розподіл варіант не відповідає нормальному закону), то група підібрана неправильно, і не може брати участь у подальших дослідженнях. Потрібно переглянути склад групи.
Однорідність і однотипність групи визначається за коефіцієнтом варіації (V), який розраховується за формулою:
V= (σ /  ) ×100%,
) ×100%,
де σ ‑ середнє квадратичне відхилення;
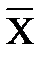 ‑ середнє арифметичне значення.
‑ середнє арифметичне значення.
Середнє квадратичне відхилення (σ) – основна характеристика варіаційного ряду, яка показує відхилення від середнього арифметичного значення. Чим менше значення σ, тим група більш однорідна й однотипна. За σ можна визначити перевагу тій або іншої методики тренування, розвитку фізичної якості, або підготовленості. За допомогою середнього квадратичного відхилення можна записати припустимі границі ( 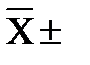 σ) для досліджуваної вибірки.
σ) для досліджуваної вибірки.
Розраховується середнє квадратичне відхилення за формулою:

де σ² - дисперсія.
Дисперсія показує розсіювання результатів і визначається за формулою:
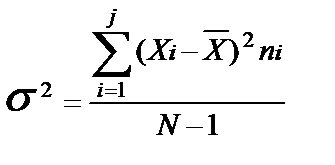
де Хі – варіанта, 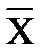 – середнє арифметичне значення, ni – частота варіанти, N – обсяг вибірки.
– середнє арифметичне значення, ni – частота варіанти, N – обсяг вибірки.
Помилка середнього арифметичного значення (m) або випадкова помилка вимірів виникає по причинах, що можна проектувати, але не можливо заздалегідь передбачити (погодні умови; напруга в мережі, від якої працює прилад…).
У залежності від обсягу вибірки, помилка середнього арифметичного значення може бути розрахована за формулою:
m = σ/ 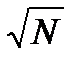 , якщо N > 20; або m = σ/
, якщо N > 20; або m = σ/  , якщо N £ 20,
, якщо N £ 20,
де N – обсяг вибірки.
Оцінка однорідності й однотипності проводиться за коефіцієнтом варіації:
якщо V ≤ 10%, то коливання результатів дослідження невелике, групу можна вважати однорідною й однотипною за своїм складом, вона може брати участь у подальших дослідженнях;
якщо V приймає значення від 10 до 20% ‑ середнє коливання результатів, групу не можна вважати однорідною і однотипною, але склад такої групи можливо переглянути;
якщо V > 20% ‑ коливання результатів велике і така група не однорідна і не однотипна, і не може брати участь у подальших дослідженнях.
Вибірковий метод. Порівняння двох середніх арифметичних за допомогою критерію Стьюдента. Достовірність різниць. Причини достовірності різниць. Ефективність тренувального процесу, переважність методик, підготовленість спортсменів.Порівняння двох вибіркових характеристик варіації за критерієм Фішера. Модельні характеристики.
Традиційно завдання фізичної культури і спорту складаються таким чином, що в їх основі лежать ідеї вибіркового методу. Основний зміст методу зводиться до того, що дослідженню підлягає генеральна сукупність не в повному обсязі, а своєю репрезентативною частиною – вибірковою сукупністю. Передбачається, що вибірка з належною вірогідністю відображує генеральну сукупність тільки у тому випадку, якщо її елементи обрані з генеральної нетенденційно.
Що стосується обсягу вибірки, то відповідно до основних положень математичної статистики, вибірка тим більш репрезентативна, чим вона повніше. У кожному конкретному випадку кількість об’єктів, що відбираються у вибірку, призначається індивідуально.
Основним завданням вибіркового методу є пошук двох показників – середнього арифметичного значення ( 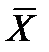 ) генеральної сукупності і середнього квадратичного відхилення (s) генеральної сукупності.
) генеральної сукупності і середнього квадратичного відхилення (s) генеральної сукупності.
У практиці спорту прийнято обирати надійність Р = 0,95 і відповідний до неї рівень значущості α= 0,05, які відображають основну групу досліджуваних завдань. У виняткових випадках при необхідності різко збільшити надійність розрахунків приймається Р = 0,99 і α = 0,01.
Велику групу завдань вибіркового методу класифікують як групу порівняльних завдань. Порівнюються дві, або більше вибіркові сукупності. При порівнянні встановлюється, належать ці вибірки до однієї і тієї ж генеральної сукупності, чи до різних. Це має значення при визначенні вірогідності різниць між двома вибірковими середніми арифметичними.
Отже, при роботі вибірковим методом у практиці фізичної культури і спорту можна знайти основні середньостатистичні показники великої групи випробуваних за допомогою вивчення малого числа їхніх представників. А також можна виявити, чи принципова різниця між кількома однотипними групами об’єктів.
За допомогою вибіркового методу математичної статистики можна оцінити:
1. Ефективність навчально-тренувального або навчально-виховного
процесу.
2. Рівень підготовленості спортсмена або групи спортсменів.
3. Перевагу або ідентичність методики навчання рухових умінь і навичок, розвитку фізичних якостей.
4. Необхідність введення нового педагогічного чинника в навчально-виховний або навчально-тренувальний процес.
Вибірковий метод дозволяє порівнювати:
· показники спортсмена або групи спортсменів однієї спеціалізації і кваліфікації до і після серії тренувальних занять для виявлення зрушень у цих показниках;
· показники фізичного розвитку, фізичної підготовленості, фізичної роботоздатності основних систем організму у спортсменів і осіб, що не займаються спортом;
· показники спортсменів, які тренуються в різних умовах або за різними методиками.
Для визначення вірогідності різниці між вибірковими середніми арифметичними необхідно обробити числа обох груп, які порівнюються, способом варіаційних рядів, тобто визначити в обох групах середнє арифметичне значення( 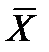 ), середнє квадратичне відхилення (s) і помилку середнього арифметичного значення (m).
), середнє квадратичне відхилення (s) і помилку середнього арифметичного значення (m).
Критерієм визначення вірогідності різниць є величина, обумовлена за формулою в залежності від того, які вибірки порівнюються в процесі дослідження – пов’язані або непов’язані.
Критерій вірогідності різниць – критерій Стьюдента (tр) розраховується за формулою:

tр=
Критерій Стьюдента (tр) -порівнюється із граничним (табличним) значенням tгр, яке визначається за спеціальною таблицею Стьюдента для конкретної надійності і обсягу вибірки. Для визначення tгр за таблицею необхідно знати к (число ступенів свободи варіації), яке розраховується за формулою:
· у випадку, якщо дорівнюються обсяги вибірок Nх = Nу, а середні квадратичні відхилення не дорівнюютьсяsх2≠sу2
к = 2*N–2
· у випадку, якщо не дорівнюються обсяги вибірок Nх≠Nу або дорівнюються середні квадратичні відхилення sх2= sу2
к = Nх + Nу –2
При порівнянні двох вибіркових середніх арифметичних, звичайно, перевіряється припущення, що і перша, і друга вибірки належать до однієї генеральної сукупності, і, отже, значною мірою не відрізняються одна від одної (порівнюються за одним показником два спортсмени, дві групи). У такому випадку бувають відомі такі статистичні характеристики: 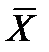 ,
,  , sх2, sу2і обсяги вибірок Nх і Nу.
, sх2, sу2і обсяги вибірок Nх і Nу.
Для відповіді на питання щодо вірогідності і не вірогідності різниць вибірок, які підлягають дослідженню, необхідно порівняти tрозрахункове (tр), і постійне граничне (tгр).
Якщо tр ≥ tгр – різниця між порівнюваними вибірковими середніми арифметичними вірогідна (не випадкова), істотна і пояснюється впливом визначених чинників, а якщо tр<tгр - не вірогідна (випадкова).
Причини вірогідних різниць при порівнянні двох вибіркових середніх арифметичних:
1. Краща підготовленість одного із спортсменів або однієї із груп.
2. Одна з досліджуваних методик навчання руховим умінням і навичкам, або розвитку рухових якостей краща, найбільш ефективна.
3. Ефективно побудований навчально-тренувальний або навчально-виховний процес.
4. При застосуванні тієї ж самої методики тренування в різних умовах – причина в тому, що одні умови кращі, ніж інші.
5. При введенні в навчально-виховний або навчально-тренувальний процес нового педагогічного чинника з метою виявлення ефективності його використання – причина в ефективності застосування експериментального педагогічного чинника.
Причини невірогідних різниць при порівнянні двох вибіркових середніх арифметичних:
1. Неправильний добір вибірки.
2. Недостатня чисельність вибірки.
3. Однаковий рівень підготовленості обох груп, які підлягають дослідженню, або обох спортсменів.
4. Неефективно побудований навчально-тренувальний або навчально-виховний процес.
5. У випадку порівняння двох методик навчання рухових умінь і навичок, або розвитку рухових якостей – ефект однаковий, методики ідентичні, не має значення за якою методикою працювати.
6. При введенні в навчально-тренувальний або навчально-виховний процес нового педагогічного чинника з метою виявлення ефективності його застосування – причина в негативному впливі нового педагогічного чинника на ефективність навчально-тренувального або навчально-виховного процесу.
7. У випадку застосування однієї методики в різних умовах, причина в однаковому результаті при тренування в різних умовах, немає істотних різниць, у яких умовах застосовувати досліджувану методику.
Для порівняння двох вибіркових характеристик варіації необхідно знати розрахункове значення критерію Фішера /F/ і критичне значення теоретичного розподілу Фішера /Fгр/.
Основні властивості критерію Фішера:
1. За даним критерієм порівнюються різні за обсягом малі й середні вибірки.
2. При порівнянні за даним критерієм дотримання нормального закону розподілу (вірності підбору групи) необов'язково, але спеціалізація і стать повинні бути однаковими.
3. За даним критерієм вибірки порівнюються на стабільність.
4. Розрахункове значення критерію Фішера розраховується за формулою:
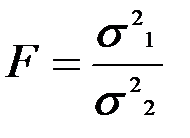
5. Критичне значення теоретичного розподілу Фішера - Fкритич визначається за таблицею. Для цього необхідно знати число ступенів свободи більшої та меншої дисперсії /k1 і k2/.
k1 і k2 розраховують за формулами:
k1 = N1 -1, де N1 - обсяг вибірки більшої дисперсії.
k2 = N2 -1, де N2 - обсяг вибірки меншої дисперсії.
За числом ступенів свободи більшої й меншої дисперсії визначаємо за таблицею критичне значення теоретичного розподілу Фішера Fгр на перетинанні k1 і k2
5. Якщо F > Fгр , то розходження між двома вибірками вірогідні (не випадкові). Якщо F ≤ Fгр, то розходження між двома вибірками не вірогідні (випадкові).
Модельні характеристики‑ це ідеальні характеристики стану спортсмена, у якому він може показати результати, що відповідають вищим світовим досягненням.
Знати модельні характеристики необхідно для визначення напрямків тренувальної роботи і проведення відбору спортсменів.
Модельні характеристики поділяються на:
а) консервативні (не піддаються тренуванню, наприклад, розміри тіла вдовжину) і неконсервативні (що змінюються під впливом тренування, наприклад, силові якості);
б) компенсуємі й некомпенсуємі;
в) етапні.
Компенсуємі - показники, низький рівень яких може бути компенсований високим рівнем інших показників. Наприклад, низька ефективність баскетболіста в грі під щитом, яка пов'язана з його невисоким ростом, може компенсуватися точністю кидків з далекої відстані так, що загальне число закинутих м'ячів буде досить високим.
Некомпенсуємі - показники, низький рівень яких не можна компенсувати високим рівнем іншого показника. Наприклад, низький рівень будь якого з показників серцево – судинної системи у лижника-гонщика не може бути компенсований ніякою технікою.
У переважній більшості випадків ми зустрічаємося із частково компенсуємими показниками: невеликі відставання в розвитку однієї якості компенсуються, великі - ні.
Існує три основних шляхи визначення модельних характеристик:
1. Дослідження спортсменів високого класу.
2. Розрахунок, так званих, належних показників.
3. Прогнозування модельних характеристик.
Якщо немає можливості визначити величини модельних характеристик переліченими шляхами, використовують метод експертних оцінок.
Середня арифметична генеральної сукупності  ген визначається у відповідності з нижніми і верхніми межами довірчих інтервалів:
ген визначається у відповідності з нижніми і верхніми межами довірчих інтервалів:
 виб - mt ≤
виб - mt ≤  ген ≤
ген ≤  виб + mt, де: (1)
виб + mt, де: (1)
 виб - середня арифметична вибіркової сукупності;
виб - середня арифметична вибіркової сукупності;
m - помилка репрезентативності;
t - критерій надійності, тобто показник обраної довірчої імовірності.
Помилка репрезентативності показує відхилення параметрів вибірки, зокрема, середньої арифметичної, від відповідних параметрів генеральної сукупності. Про величину цієї помилки можна говорити з певною імовірністю, на величину якої вказує критерій t.
Величина помилки репрезентативності може бути знайдена в такий спосіб:
 для n < 20 (2)
для n < 20 (2)
 , де (3)
, де (3)
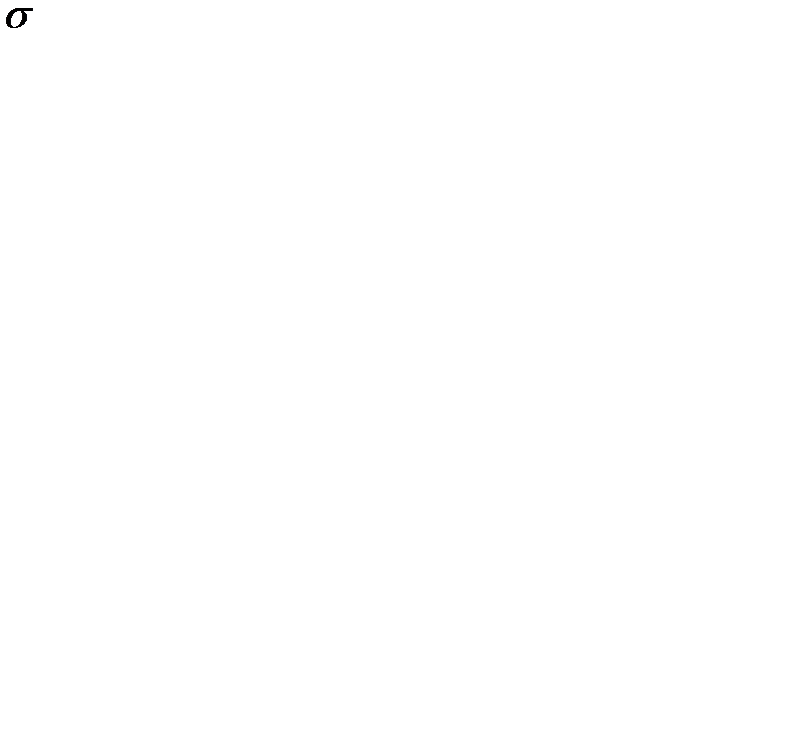 виб - середнє квадратичне відхилення вибіркової сукупності;
виб - середнє квадратичне відхилення вибіркової сукупності;
n - обсяг вибірки;
N - обсяг генеральної сукупності.
 для n > 20 (4)
для n > 20 (4)
Помилка репрезентативності у відповідності з формулою для досить великих N спрощується:
 (3а)
(3а)
Значення критерію вірогідності відповідає довірчий імовірності і визначається за таблицею Стьюдента.
У спортивній практиці використовуються такі надійності:
P1 = 0,95 і Р2 = 0,99
Середнє квадратичне відхилення генеральної сукупності ( 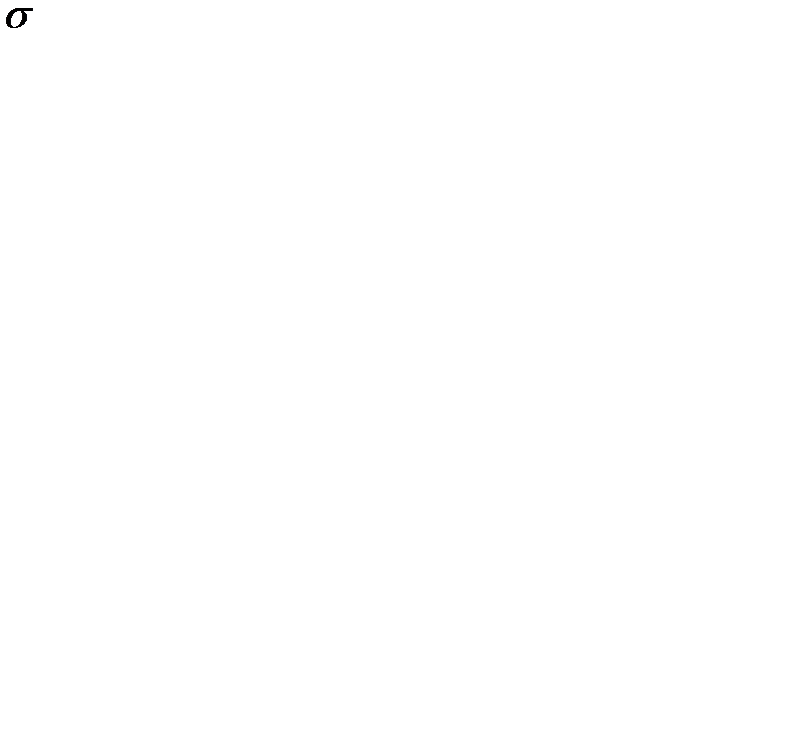 ген) визначається з наступної нерівності:
ген) визначається з наступної нерівності:
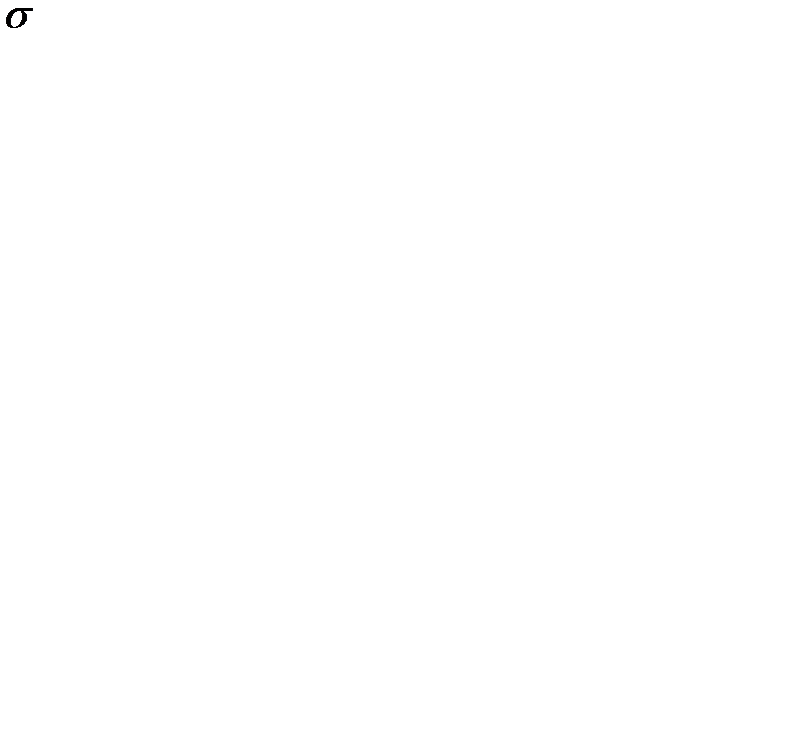 виб(1 - q) ≤
виб(1 - q) ≤ 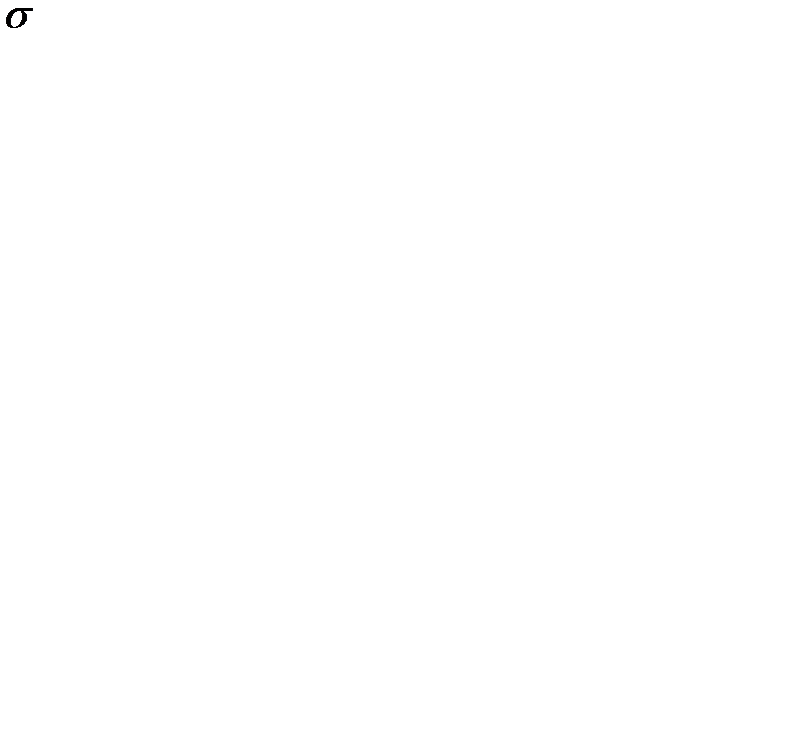 ген≤
ген≤ 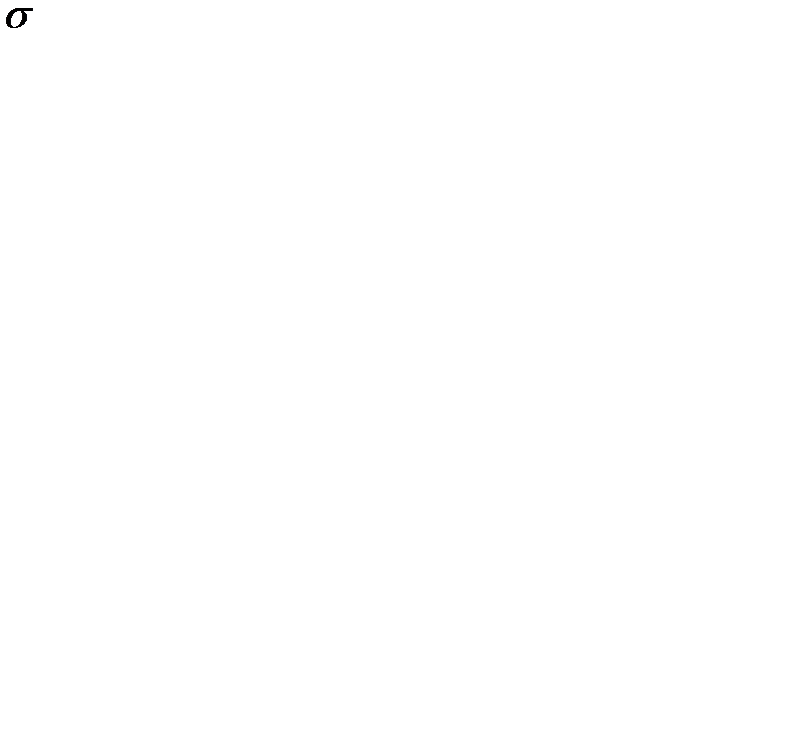 виб(1 + q) , де: (5)
виб(1 + q) , де: (5)
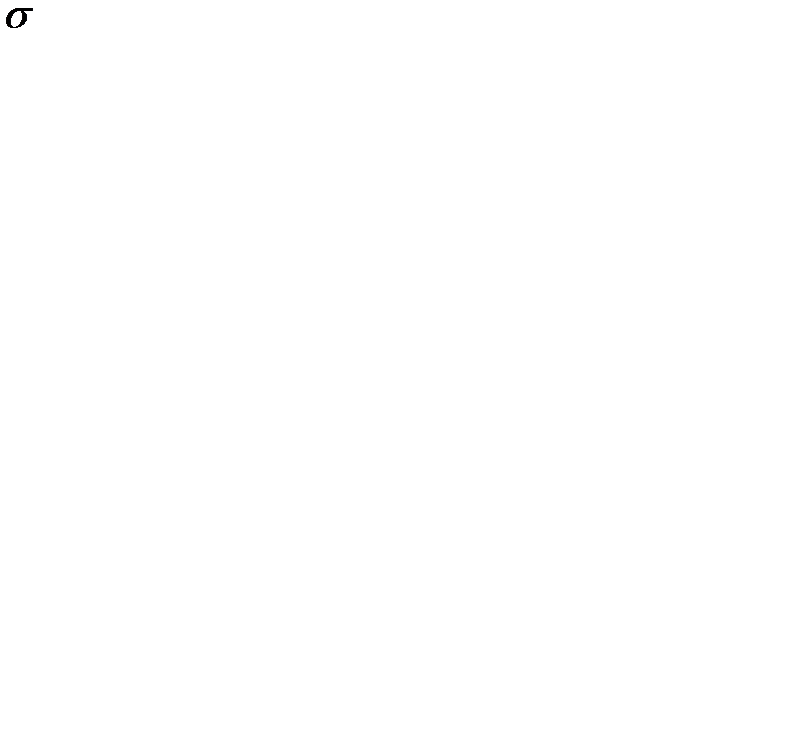 виб - середнє квадратичне відхилення вибіркової сукупності;
виб - середнє квадратичне відхилення вибіркової сукупності;
q – величина, яка визначається за таблицею.
Таблиця значень q для визначення довірчих інтервалів 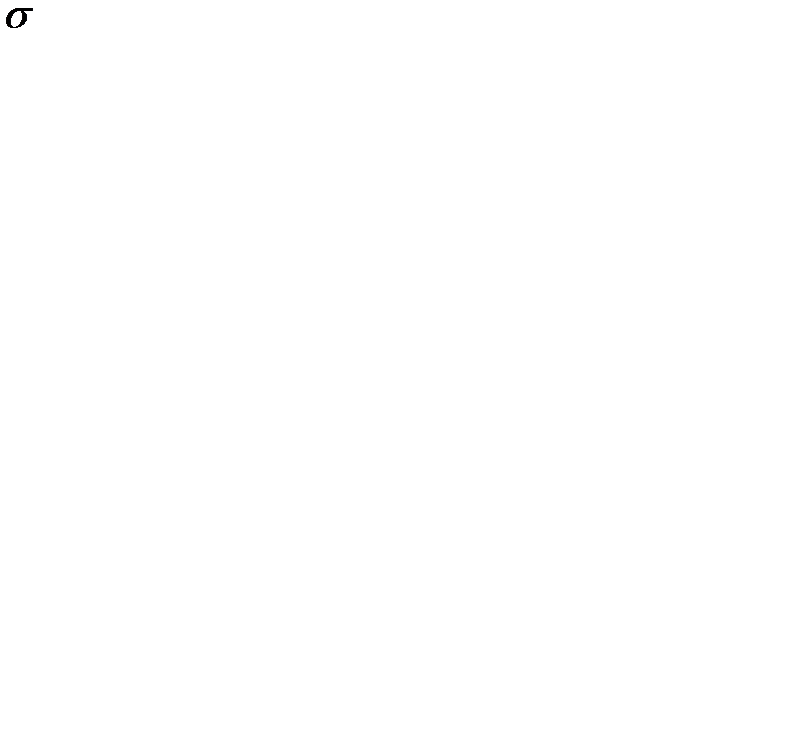 генерального.
генерального.
Надійність Р = 0,95, n – обсяг вибірки.
| n | q | n | q | n | q |
| 5 | 1,37 | 15 | 0,46 | 45 | 0,22 |
| 6 | 1,09 | 16 | 0,44 | 50 | 0,21 |
| 7 | 0,92 | 17 | 0,42 | 60 | 0,188 |
| 8 | 0,80 | 18 | 0,40 | 70 | 0,174 |
| 9 | 0,71 | 19 | 0,39 | 80 | 0,161 |
| 10 | 0,65 | 20 | 0,37 | 90 | 0,151 |
| 11 | 0,59 | 25 | 0,32 | 100 | 0,143 |
| 12 | 0,55 | 30 | 0,28 | 150 | 0,115 |
| 13 | 0,52 | 35 | 0,26 | 200 | 0,099 |
| 14 | 0,48 | 40 | 0,24 | 250 | 0,089 |
Кореляційний аналіз. Визначення залежності між двома вимірюванними показниками. Коефіцієнт кореляції. Взаємозв’язок між двома вимірюваними величинами, форма та спрямованість взаємозв’язку. Кореляційне поле. Знаходження найбільш імовірних лінійних залежностей між двома факторами (побудова прямих регресій).
У спортивних дослідженнях між досліджуваними показниками часто спостерігається взаємозв’язок. Вид його може бути різним. Розрізняють два види взаємозв’язку: функціональний і стохастичні.
Функціональний взаємозв’язок‑ це залежність, при якій кожному значенню одного показника відповідає строго визначене значення іншого і ні якої варіації бути не може.
До другого виду взаємозв’язку належить, наприклад, залежність маси тіла від довжини тіла. Одному значенню довжини тіла може відповідати декілька значень маси тіла і навпаки. У таких випадках, коли одному значенню одного показника відповідає декілька значень іншого показника, взаємозв’язок називається стохастичним.
Вивченню статистичного взаємозв’язку між різними показниками в спортивних дослідженнях приділяють велику увагу, тому що це дозволяє розкрити деякі закономірності і надалі описати їх як за допомогою слів, так і математичних знаків та формул, з метою застосування в практичній роботі тренера і педагога.
Серед статистичних взаємозв’язків найбільш важливі ‑ кореляційні (від латинського Correlatio - співвідношення, відповідність).
Кореляція - вид взаємозв’язку між ознаками. Кожна ознака являє собою велику кількість однотипних показників, що варіюють.
Кореляція полягає в тому, що середня величина одного показника змінюється в залежності від середньої величини іншого.
Статистичний метод, що застосовується для дослідження взаємозв’язків, називається кореляційним аналізом. Головне завдання кореляційного аналізу - визначення форми, щільності, спрямованості досліджуваних показників. Він широко застосовується в теорії тестів для оцінки їхньої надійності й інформативності.
За допомогою кореляційного аналізу можна оцінити:
1. Взаємозв’язок між спортивними результатами і функціональними показниками (результат у бігу на 100 м і кількість лактату в крові);
2. Вплив спортивної діяльності на результат (результат у човниковому бігу 3×100 м і результат у бігу на 100 м);
3. Взаємний вплив показників тренованості (результат при проходженні 10×200 м і результат при проходженні середньої дистанції, у плаванні);
4. Надійність тесту (погодженість, стабільність);
5. Інформативність тесту (залежність між кількістю гребків за 30 секунд і часом проходження дистанції 100 м у плаванні).
Аналіз взаємозв’язку починається із графічного представлення результатів вимірів у прямокутній системі координат. Графічна залежність має назву «діаграма розсіювання» або «кореляційне поле». Візуальний аналіз кореляційного поля дозволяє виявити спрямованість і форму залежності (принаймні, зробити припущення).
За кореляційним полем можна визначити спрямованість:
а) пряма позитивна кореляційна статистична залежність (нахил кореляційного поля вправо) (рис. 2). Зі зростанням (зменшенням) першої ознаки (Хі) інший (Уі) також зростає (зменшується).
б) обернено-негативна кореляційна статистична залежність (нахил кореляційного поля вліво) (рис. 3). Зі зростанням першої ознаки (Хі) інший (Уі) зменшується і навпаки, зі зменшенням першої ознаки (Хі) інший (Уі) зростає.
Якщо кореляційне поле подане окружністю, то залежність відсутня (рис. 4).
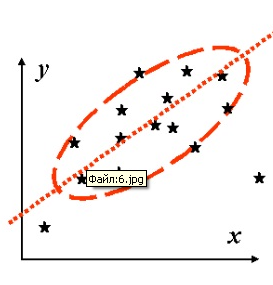
Рис. 2. Пряма позитивна кореляційна статистична залежність
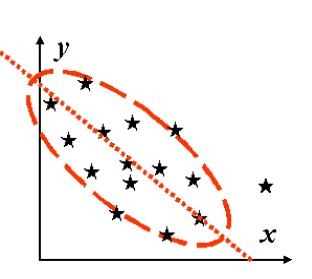
Рис. 3. Обернено-негативна кореляційна статистична залежність

|
Рис. 4. Статистична залежність відсутня
Якщо кореляційне поле подане прямою лінією, то має місце функціональна залежність
Форми статистичної залежності:
1. Лінійна форма залежності ‑ форма є близькою до звичайної геометричної фігури – еліпсу.
2. Нелінійна форма залежності ‑ будь-яка інша форма, крім еліпса.
Отже, візуальний аналіз кореляційного поля дозволяє виявити форму статистичної залежності ‑ лінійну або нелінійну. Це має істотне значення для наступного кроку в аналізі ‑ вибору й обчисленні відповідного коефіцієнта кореляції.
Для більш точної оцінки кореляції, що визначається за формулою, потрібно знати форму залежності:
1. Якщо виміри проводяться за шкалою відношень або інтервалів, і форма залежності лінійна, то коефіцієнт кореляції розраховується за формулою Браве-Пірсона (rxy) :
 rxy , де
rxy , де
Хі й Уі - варіанти 2-х вибірок;
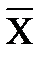 і
і 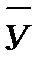 ‑ середнє арифметичне значення показників Хі й Уі;
‑ середнє арифметичне значення показників Хі й Уі;
σх, σу ‑ середнє квадратичне відхилення;
N ‑ число вимірів (випробуваних).
 2. Якщо виміри проводяться за шкалою відношень або інтервалів, і форма залежності нелінійна, коефіцієнт кореляції (rxy) розраховується за формулою:
2. Якщо виміри проводяться за шкалою відношень або інтервалів, і форма залежності нелінійна, коефіцієнт кореляції (rxy) розраховується за формулою:
rxy
Для оцінки щільності взаємозв’язку в кореляційному аналізі застосовується значення спеціального показника ‑ коефіцієнта кореляції (rxy).
Абсолютне значення коефіцієнта кореляції знаходиться в межах від 0 до 1 - пряма позитивна кореляційна статистична залежність і від (-1) до 0 - обернена негативна кореляційна статистична залежність:
-1 £rxy£ 1
Пояснюють значення цього коефіцієнта в такий спосіб:
а) rxy = 1 зв’язок між ознаками дуже щільна (функціональний взаємозв’язок);
б) rxy = 0 зв’язок між ознаками Хі й Уі відсутній;
в) чим ближче значення rxy до нуля, тим зв’язок слабкіше, чим ближче значення rxy до одиниці‑- тим щільніше.
Прийнято вважати, що
rxy = 0,2....0,49 ‑ слабкий зв’язок;
rxy = 0,5....0,69 ‑ середній зв’язок;
rxy = 0,7....0,99 ‑ тісний (сильний) зв’язок.
На кореляційному полі щільність може виглядати так:
а) якщо точки групуються вздовж якої-небудь лінії, то зв’язок є, і він тим щільніше, чим ближче вони групуються.
б) якщо точки розсіяні хаотично, зв’язок між ознаками відсутній або дуже слабкий.
Проте, варто пам’ятати, що при роботі з великою точністю, наприклад, при оцінці кореляцій спортсменів високої кваліфікації, коефіцієнт кореляції відображає щільний зв’язок, якщо він не менше 0,9.
У деяких випадках щільність взаємозв'язку визначають на підставі коефіцієнта детермінації (D), що розраховують за формулою:
D = r²×100 %
Цей коефіцієнт визначає частину загальної варіації одного показника, що пояснюється варіацією іншого показника. Залишок відсотків варіації від ста пояснюється впливом іншихчинників.
У випадку лінійного взаємозв'язку між двома ознаками (факторами), тобто коли кореляційне поле має форму еліпса, за допомогою коефіцієнта кореляції можна знайти найбільш імовірні лінійні залежності, тобто рівняння регресії, які є рівняннями прямої лінії.
Таких рівнянь два:
у = а1 +ву/х×х - пряме;
х = а2 + вх/в × у - зворотне,
де а і в - коефіцієнти, або параметри, які слід визначити.
Значення коефіцієнтів регресії обчислюється за формулою:
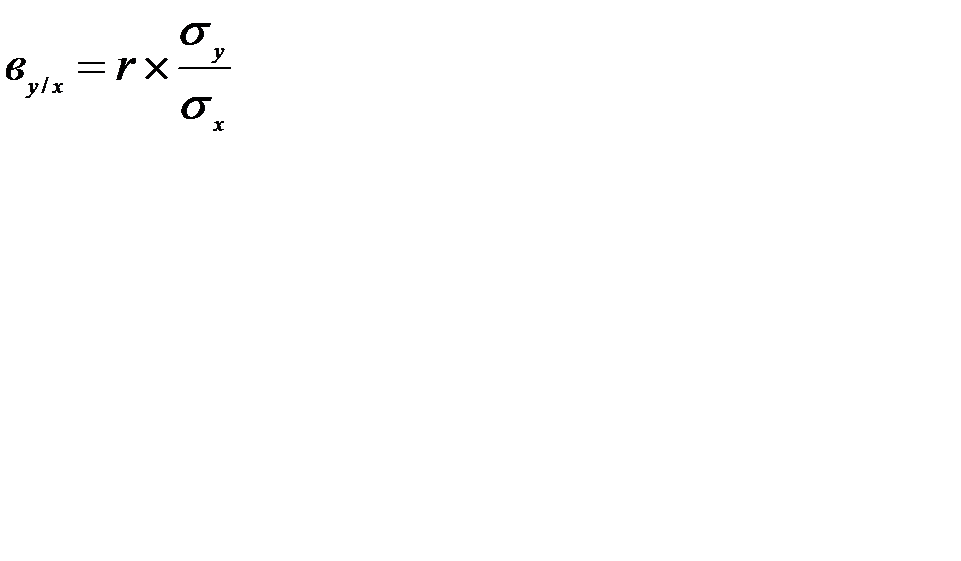 і
і 
Коефіцієнт регресії в має розмірність, яка відповідає відношенню розмірностей досліджуваних показників X і У, і той же знак, що й коефіцієнт кореляції.
Коефіцієнт а визначається за формулою:
а1=  - ву/х ×
- ву/х ×  ;
;
а2=  - ву/х ×
- ву/х × 
Для того, щоб обчислити цей коефіцієнт, треба просто в рівняннях регресії підставити середні значення змінних величин, які корелюють.
Для оцінки точності рівняння регресії розраховується залишкове середнєквадратичневідхилення за формулою:


Ці оцінки абсолютні і, отже, не можуть бути порівнянні один з одним. Тому застосовують оцінки відносної похибки рівнянь, які мають бути виражені у відсотках і визначаються за формулою:


Значення цієї оцінки, якщо r = ±1,00, дорівнює нулю і, якщо r = 0,00, максимальне.
Залишкове середнєквадратичневідхилення характеризує коливання У, щодо лінії регресії з X у прямому рівнянні регресії і, навпаки, у оберненому випадку.
Ряди динаміки.Відображення у часі явища, що підлягає дослідженню; його оцінка й прогнозування за допомогою рядів динаміки. Статистична крива. Основні характеристики рядів динаміки. Абсолютний приріст, темп росту, темп приросту. Аналіз і прогноз явища.
Ряди динаміки відображають розвиток явища або процесу у часі. Вони являють собою співвідношення рівнів, тобто показників вимірюваного процесу, і періодів часу, протягом яких ці рівні були фіксовані.
На підставі рядів динаміки можливе рішення двох принципових задач: аналізу й прогнозу. Аналіз відбувається для будь-якого явища, представленого вимірами результатів, що змінюються із часом. Особливо важливий подібний аналіз у дослідженнях дитячого та юнацького спорту, де зміни досліджуваних параметрів відбуваються не тільки під впливом тренувальних навантажень, але й відповідно до розвитку організму.
Прогноз спортивних процесів відбувається тільки в тому випадку, якщо його результати мають безпосереднє відношення до подальшої роботи з досліджуваним: прогноз спортивного результату, стан тренованості, прогноз розвитку якої-небудь якості, тощо.
У деяких випадках має сенс на тому самому емпіричному матеріалі поєднувати задачі аналізу й прогнозу.
За допомогою рядів динаміки можливо:
1. Аналізувати й прогнозувати властивості досліджуваних.
2. Аналізувати й прогнозувати властивості індивіда.
3. Оцінити й передбачити вікові зміни.
4. Відобразити біомеханічні змінні.
Як правило, ряди динаміки відображають у вигляді графіків, таблиць і формул. Найбільш простий спосіб побудови рядів динаміки - графічний.
Наприклад, школярі були досліджені за величиною середньостатистичної станової сили, Н кг (ньютон на 10 кг маси) в 9, 10, 11:12 і 13 років. Представити ці зміни динамічним рядом.
| ti | 9 | 10 | 11 | 12 | 13 |
| Уі | 89,2 | 91,6 | 94,4 | 97,0 | 98,6 |
Розглянемо Уі як рівні динамічного ряду, фіксовані в період часу ti. За цими даними необхідно побудувати графік Уі = t(ti), на якому рівні отриманого динамічного ряду будуть відкладені за відповідними періодами часу в системі прямокутних координат. Якщо знайдені точки з'єднати послідовно відрізками прямих, одержимо статистичну криву‑ лінію, що відображає реальну зміну досліджуваного явища у часі. Статистична крива дозволяє оцінювати досліджуваний процес у динаміці.
Основними характеристиками динамічного ряду є:
- абсолютний приріст У,
- темп росту Т,
- темп приросту Тпр.
Абсолютний приріст - це різниця між наступним Уі і попереднім Уі-1 рівнем ряду: У = Уі- Уі-1
Абсолютний приріст може бути позитивним - указувати на зростання досліджуваного явища із часом і негативним - на убування.
Темп росту динамічного ряду є відношення наступного рівня до попереднього. Якщо рівні належать до одного й того ж вихідного (базисного) рівня, вони називаються базисними,при послідовному відношенні наступного до попереднього - ланцюговими.
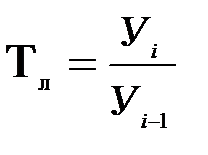 - ланцюговий темп росту
- ланцюговий темп росту
 - базисний темп росту
- базисний темп росту
Темп росту за весь період - це відношення наступного рівня до базисного:
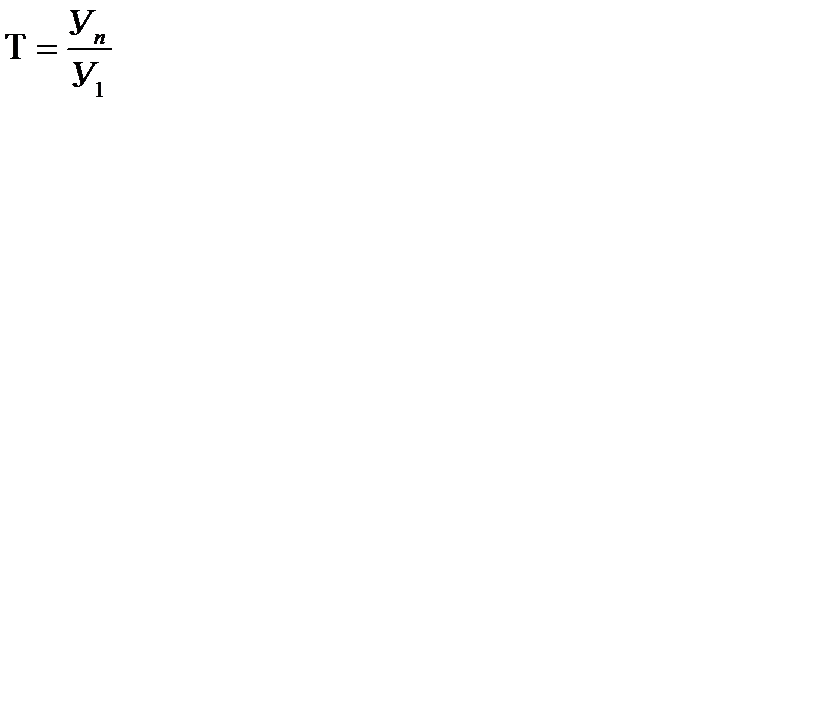 - темп росту за весь період .
- темп росту за весь період .
Темп приросту - відношення абсолютного приросту ∆У до базисного рівня Уі-1 :
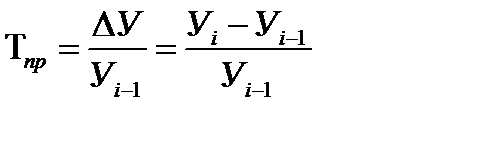
Як відображено на рисунку, статистична крива являє собою ламану лінію, вузлові точки якої коливаються щодо якогось напрямку. Визначення цього напрямку - тенденції (тренда) - це визначення тих рівнів, які адекватні вихідним даним. У сутності тенденція є закономірність, відповідно до якої змінюється у часі досліджуване явище. Така закономірність дозволяє вирішити два принципових завдання:
1) з її допомогою можна оцінити досліджуване явище;
2) можна його прогнозувати.
У такій ситуації рішення зводиться до виявлення тенденції й роботі з нею.
Виявлення тенденції (тренда) можливо зробити декількома способами. Одними з них є:
1) Метод рухомої середньої.
2) Метод найменших квадратів.
1. За методом рухомої середньої вихідні показники осереднюються і їхні середні значення приймаються за рівні динамічного ряду, на підставі яких будується статистична крива, що відображає зміну досліджуваного явища у часі. Таким чином, визначивши тенденцію, відповідно до якої розвивається у часі досліджуване явище, можна проводити його аналіз і прогноз.
2. Метод найменших квадратів - аналітичний спосіб виявлення тенденції. У ході алгебраїчних рівнянь визначаються коефіцієнти прямої лінії У=Во+В×Х, що відображає статистичну закономірність зміни у часі досліджуваного явища.
Во; В - коефіцієнти, і вони розраховуються за формулами:
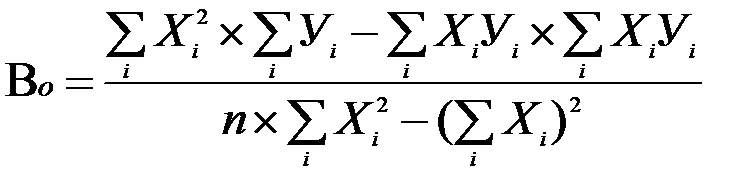 , де n - число вимірів
, де n - число вимірів

Таким чином, метод найменших квадратів дає відповідь на питання: "Як провести криву через експериментально отримані точки, щоб ця крива ближче всього підходила до істинної кривої шуканої функції?"
Не можна проводити криву за отриманими точками. А її треба провести так, щоб сума квадратів вертикальних відхилень експериментальних точок від проведеної кривої вийшла мінімальною.
Після одержання статистичної кривої можна проводити аналіз і прогнозування досліджуваного показника.
Дисперсійний аналіз. Вивчення впливу факторної ознаки, залежно від її градацій, на результативну ознаку в практиці спортивної діяльності. Оцінка тренувальних впливів. Вплив умов спортивної діяльності.
Дисперсійний аналіз ‑ це статистичний метод, за допомогою якого можна встановити вплив однієї ознаки на іншу. На відміну від кореляційного аналізу, де також визначається вплив ознак, розглядається їх більш складна структура.
Дисперсійний аналіз має перевагу надкореляційним: тут можна врахувати вплив ознаки, що не має кількісного вираження.
Ознака, що підлягає дослідженню, називається результативною (R).
Вона випробовує на собі вплив факторної ознаки F, чия структура підрозділяється на ряд підгруп, так званих градацій фактору.
Для дослідження залежності результативної ознаки від факторної обирається спеціальна вибірка, яка називається дисперсійним комплексом, із загальним числом елементів N.
Вихідні позиції методу базуються на сумі квадратів відхилень варіантів від їх середньої:
 , де (1)
, де (1)
S - сума квадратів відхилень;
Xi - варіанта вихідного ряду
ni- частота вихідного ряду;
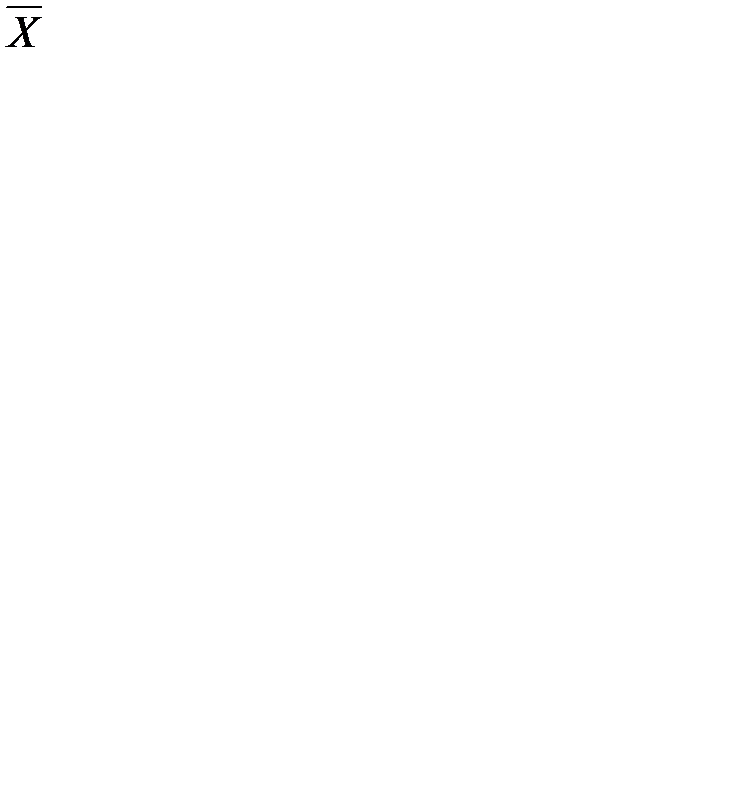 - середнє арифметичне значення вихідного ряду.
- середнє арифметичне значення вихідного ряду.
Встановлено, що сума квадратів відхилень на всій результативній ознаці Sy складається із двох додатків:
Sy = Sx + Sz (2)
де Sx - сума квадратів відхилень, обумовлена варіацією середніх арифметичних усередині градації, щодо середньої арифметичної всього комплексу.
Ця варіація враховує вплив досліджуваного фактору на результативну ознаку.
Sz‑ сума квадратів відхилень, обумовлена варіацією вихідних даних, щодо середніх арифметичних усередині кожної градації.
Ця варіація обумовлена впливом так званих випадкових причин, тобто причин, не пов'язаних з дією фактору.
Рівняння (2) є основним рівнянням дисперсійного аналізу.
Таким чином, після визначення значення Sx, Sy, Sz стає можливим оцінити загальну варіацію результативної ознаки (Sy) і її складові частини: варіацію, яка обумовлена факторною ознакою (Sx), і варіацію від випадкових причин (Sz).
Надалі необхідно перейти до порівняльного аналізу суми квадратів відхилень Sx і Sz. Аналіз проводиться за допомогою критерію Фішера.
Якщо значення варіацій, обумовлених факторною ознакою й випадковими причинами, відрізняються статистично - вірогідно, то прийдемо до висновку, що розглянута факторна ознака впливає на результативну ознаку.
У практичному використанні градації факторної ознаки помітні між собою кількісно, у якісному ж відношенні вони являють собою однозначну характеристику.
Наприклад, оцінюючи вплив вікового розвитку дітей на який-небудь показник, дисперсійний комплекс складається з результативної ознаки (досліджуваний показник) і факторної (вік дітей). При цьому вік дітей, які підлягають дослідженню, доречно розділити за віковими категоріями:
10-12 років; 13-14 років; 14-16 років, тощо.
Вони й будуть являти собою градації фактору.
Якщо задачі ускладнюються, і факторна ознака змінює свою структуру у якісному відношенні, розглядають дисперсійний аналіз двох, трьох і тощо, багатофакторних комплексів.
Практична реалізація дисперсійного аналізу:
1. Оцінка тренувальних впливів: якщо розглядати спортивний результат, або яку-небудь кількісну характеристику результату, як результативну ознаку, то обсяг тренувального навантаження, її інтенсивність або співвідношення обсягу й інтенсивності можна розглядати, як факторну ознаку.
Градаціями фактору в цьому випадку виступають різні кількісні межі обсягу і інтенсивності навантажень або їх співвідношень.
Використовуючи дисперсійний аналіз, можна оцінити вплив ознаки на кінцевий результат спортивної діяльності.
2. Вплив умов спортивної діяльності: під умовами спортивної діяльності будемо розуміти різноманітні види робіт з учасниками досліджень:
Різні програми, методики, режими, види робіт спортивних спеціалізацій, умови експерименту.
Параметр спортивної діяльності приймається, як результативна ознака.
Факторною ознакою є умови роботи спортсмена, що відрізняються різними кількісними межами - градаціями фактору.
Застосування дисперсійного аналізу приводить до оцінки впливу різноманітних умов роботи на параметр спортивної діяльності, який підлягає дослідженню.
3. Вплив біологічного й соціального факторів: у якості факторної ознаки зручно представити різноманітні біологічні й соціальні фактори: - вік, стать, різні медичні групи випробуваних, відношення до спорту, соціальні групи населення, професійні особливості.
Вихідними даними дисперсійного аналізу будемо вважати Xі - вимір практичних спортивних величин і їхньої частоти nі.
Величини Xi вимірюються за умов дії на випробуваних факторної ознаки F, що має градації F1, F2,....Fn.
Градації помітні за кількісними характеристиками. При виконанні статистичних операцій дисперсійного аналізу, в першу чергу, визначаються суми квадратів відхилень за формулами:
 , де (3)
, де (3)
Sy - загальна сума квадратів відхилень варіантів результативної ознаки;
Xi - варіанти результативної ознаки;
N - обсяг усього дисперсійного комплексу.
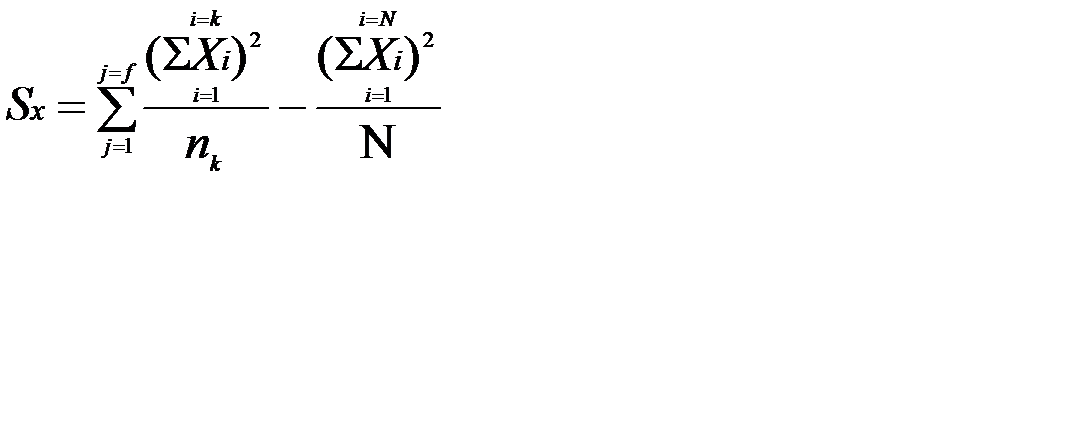 , (4) де
, (4) де
Sx - сума квадратів відхилень варіантів результативної ознаки, обумовлена впливом фактору;
і = 1,2, ....., N;
N - обсяг дисперсійного комплексу;
j = 1, 2,..., f - кількість градацій;
k - обсяг кожної градації дисперсійного комплексу.
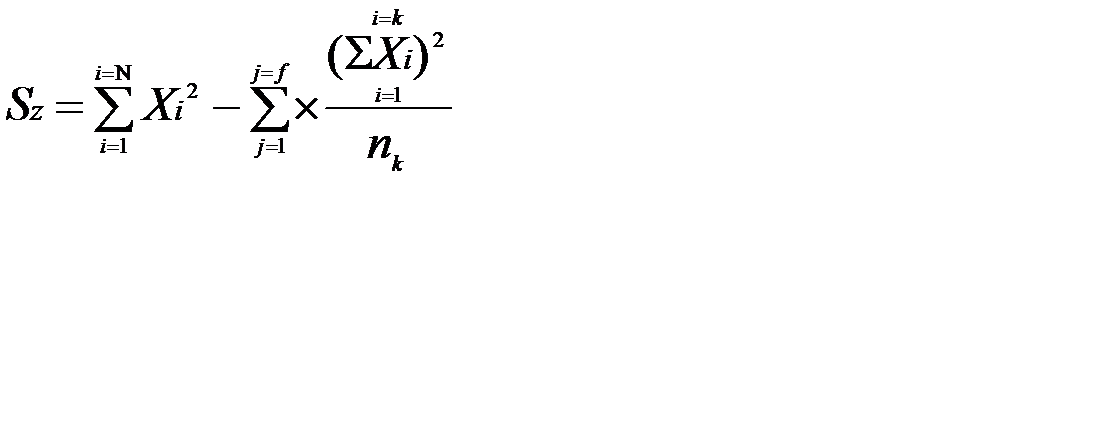 , де (5)
, де (5)
Sz - сума квадратів відхилень варіантів результативної ознаки, щообумовлена впливом випадкових причин;
j = 1, 2,..., f;
f - кількість градацій.
Для визначення Sx, Sy, Sz у практичних задачах необхідно вихідні дані й проміжні обчислення зосередити в таблиці (дивись таблицю у прикладі).
Визначивши Sx, Sy, Sz, необхідно переконатися у виконанні основного рівняння дисперсійного аналізу:
Sy = Sx + Sz, після чого, можна приступити до загальної оцінки впливу факторної ознаки на результативний за допомогою загальної суми квадратів відхилень і її складових.
Надалі приступаємо до оцінки впливу факторної ознаки на результативний за допомогою оцінки на статистичну вірогідність.
Критерій Фішера, що аналізує статистичну вірогідність (невірогідність), визначається, як частка від ділення порівнюваних дисперсій.
Таким чином, порівнюючи вплив факторної ознаки й випадкових причин, необхідно визначити дисперсії результативної ознаки, що залежать від фактору і випадку.
Для їхнього визначення необхідно знайти відповідні ступені свободи:
kу= N - 1;
kx = j - 1; (6)
kz = (N - 1) - (j - 1) = N - J, де
kу- ступені свободи загальної дисперсії;
kx- ступені свободи дисперсії, яка обумовлена фактором;
kz- ступені свободи дисперсії, яка обумовлена випадковими причинами.
Дисперсії визначаються як:

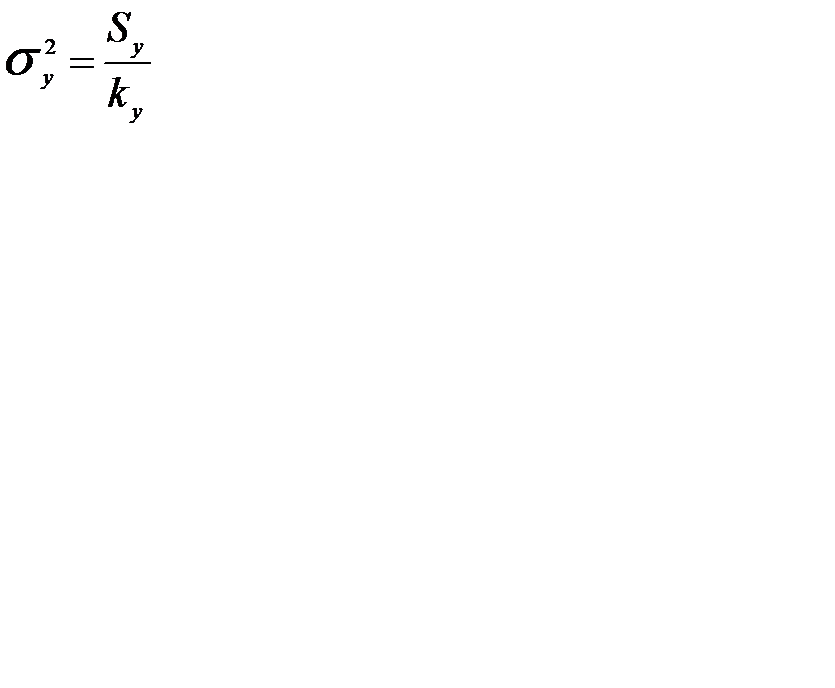 ;
; 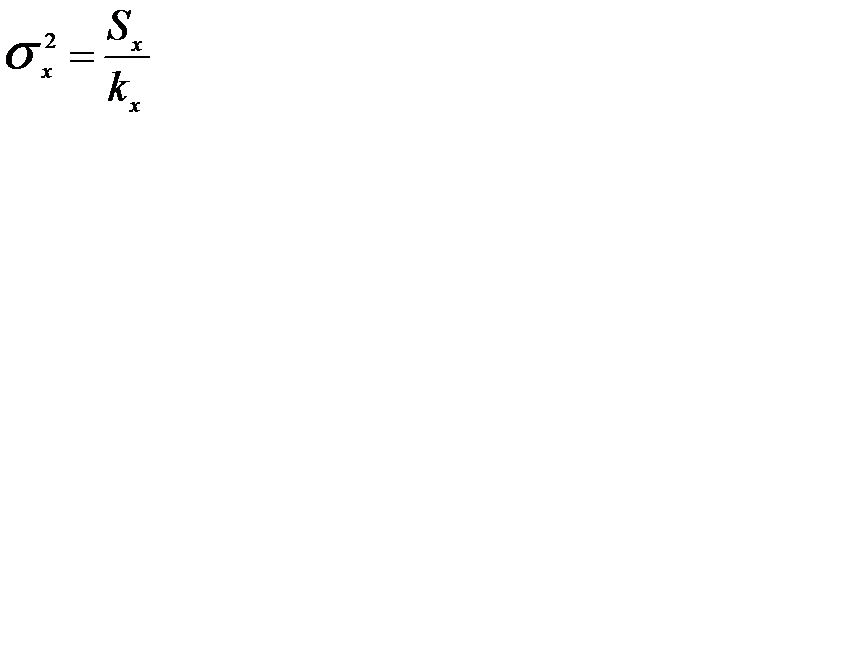 ;
; 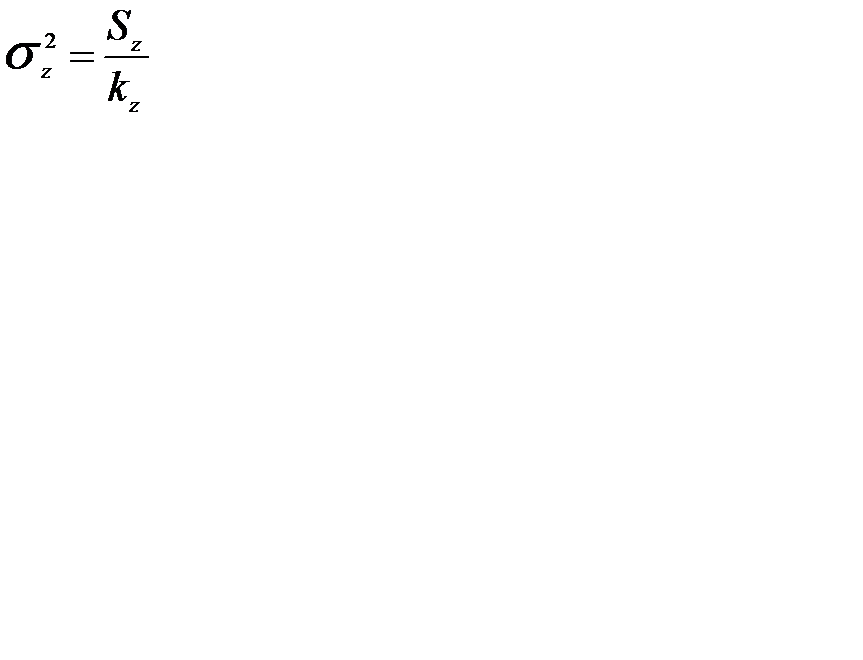 (7)
(7)
Тепер визначимо критерій Фішера:
 , де (8)
, де (8)
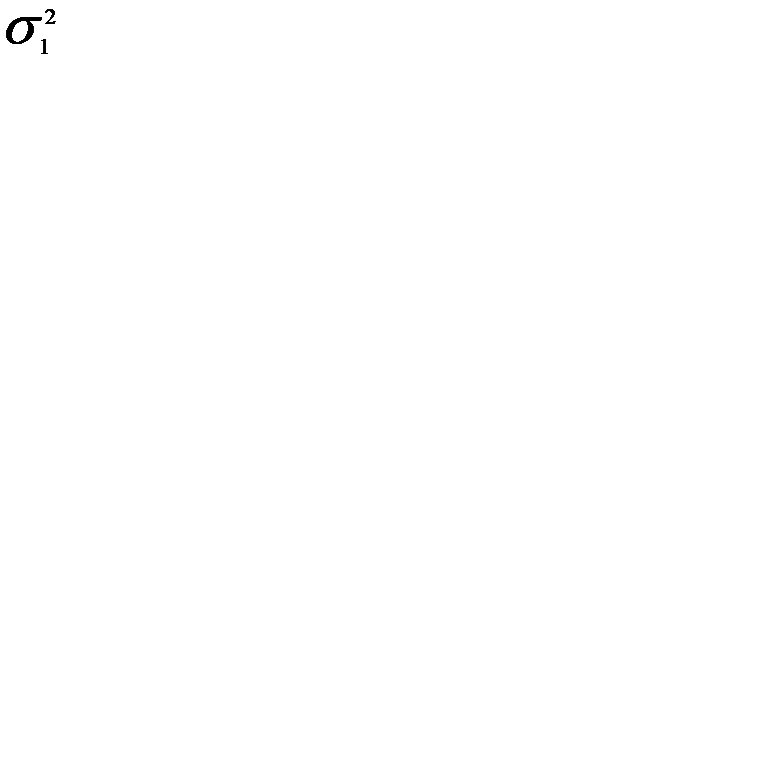 і
і 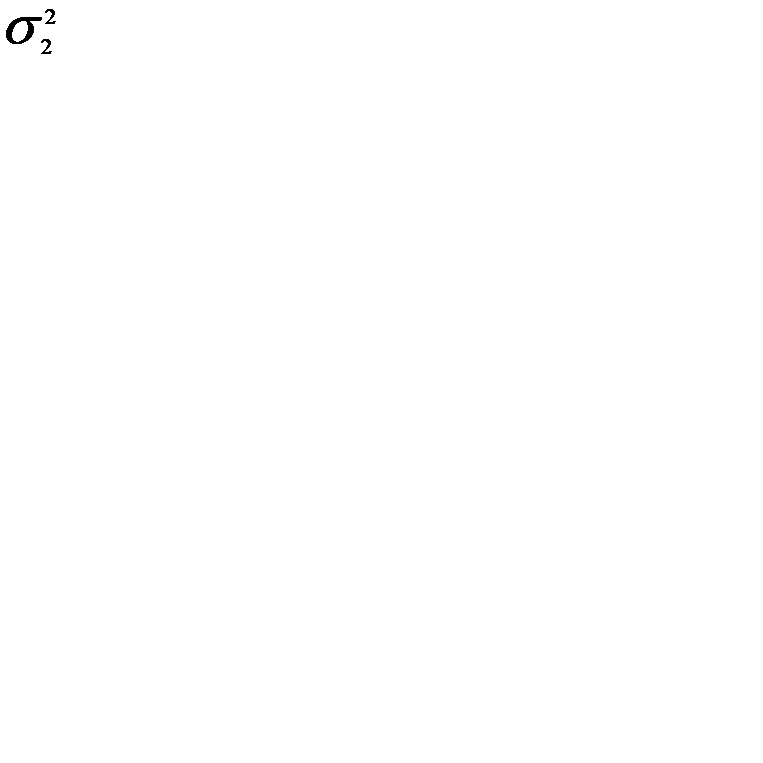 - дисперсії від факторної ознаки й від випадкових причин. Відповідно до вимог критерію Фішера, у чисельнику перебуває більша із цих дисперсій (
- дисперсії від факторної ознаки й від випадкових причин. Відповідно до вимог критерію Фішера, у чисельнику перебуває більша із цих дисперсій ( 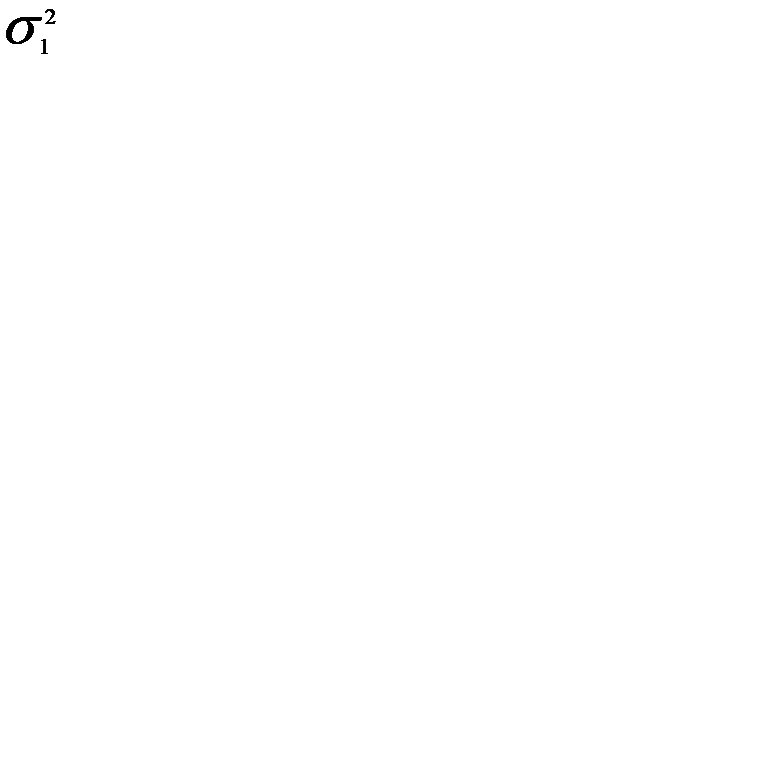 >
> 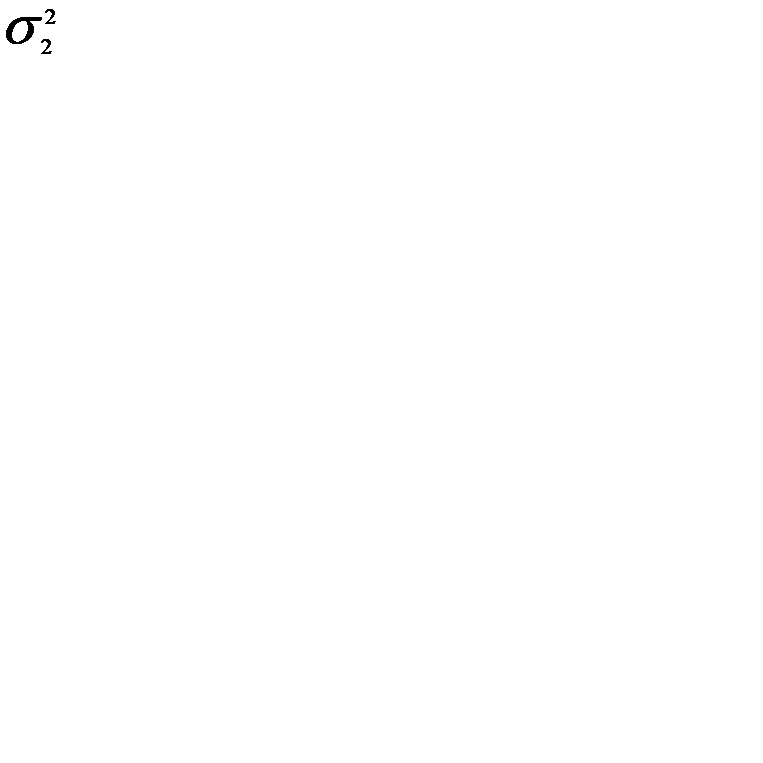 )
)
Критерій, що розрахували, порівнюється з Frp - граничним значенням критерію, який визначається за таблицею Фішера за ступенями свободи kх і kz і надійністю Р.
Проводимо порівняння F і Fгp і робимо висновок:
1 якщо F > Fгp - розходження між впливом від факторної ознаки і від випадкових причин статистично вірогідне, тобто фактор, який підлягає дослідженню впливає на результативну ознаку;
2 якщо F < Fгp - розходження статистично не вірогідне, і фактор, який підлягає дослідженнюне робить принципового впливу на результативну ознаку.
Оцінити ступінь впливу фактору,який підлягає дослідженнюна результативну ознаку можна за допомогою наступного показника:

Величина, розрахована за цією формулою, зазначає який відсоток варіації результативної ознаки визначається впливом фактору, який підлягаєдослідженню.
Питання для самоконтролю:
1. Розкрити загальні положення методу середніх величин.
2. Основні характеристики варіаційного ряду.
3. Як проводиться обрахування середнього квадратичного відхилення.
4. Назвіть характеристики які відображають варіацію показників?
5. Яким чином проводиться загальна оцінка масиву чисел за допомогою метода середніх величин.
6. Який показник відображає однорідність і однотипність групи?
7. Основні положення вибіркового методу.
8. Поняття про генеральну та вибіркову сукупність.
9. Поняття про надійність та рівень значущості.
10. За яких умов розбіжність між двома вибірками за показниками варіації буде вірогідною?
11. Основні положення кореляційного аналізу.
12. Кореляційне поле, як найпростіший засіб відображення залежності між показниками.
13. Розкрийте принцип знаходження найбільш імовірних лінійних залежностей між двома факторами.
14. Який метод математичної статистики використовується для знаходження найбільш імовірних лінійних залежностей між двома факторами?
15. За яких умов ми маємо можливість побудувати пряму регресію?
16. Який вигляд має рівняння прямої лінії?
17. Запишіть пряме і зворотне рівняння регресії.
18. Як розраховуються коефіцієнти рівнянь регресії?
19. Який показник характеризує точність рівняння регресії?
20. Як розраховується похибка рівняння залежності між двома факторами?
21. Як визначити точність рівнянь регресії?
22. Що таке ряди динаміки?
23. У якому вигляді можуть бути представлені ряди динаміки?
24. Які завдання можливо вирішити за допомогою рядів динаміки?
25. Назвіть основні характеристики рядів динаміки.
26. Дайте визначення основним характеристикам динамічного ряду.
27. На що вказує позитивний абсолютний приріст?
28. Яким чином змінюється явище у часі, якщо абсолютний приріст має негативне значення?
29. Як змінюється явище у часі, якщо темп росту динамічного ряду дорівнює одиниці.
30. Як називається лінія, що відображає реальну зміну досліджуваного явища із часом?
31. Назвіть способи виявлення тенденції (тренда) динамічного ряду.
32. Яким чином розраховується рухоме середнє арифметичне значення?
33. Розкрийте зміст методу найменших квадратів.
34. Як здійснити прогноз за допомогою метода рухомої середньої?
35. Що можливо встановити за допомогою дисперсійного (факторного) аналізу?
36. У чому полягає перевага дисперсійного аналізу перед кореляційним?
37. Як називається ознака, яка підлягає дослідженню?
38. Що називається дисперсійним комплексом?
39. Основне рівнянням дисперсійного аналізу?
40. За допомогою якого критерію проводиться порівняльний аналіз суми квадратів відхилень?
41. Однофакторні та багатофакторні дисперсійні комплекси.
42. Практична реалізація дисперсійного аналізу.
43. За якими формулами визначаємо ступені свободи дисперсій?
44. За допомогою якого показника можна оцінити ступінь впливу фактору, який підлягає дослідженню, на результативну ознаку?
Дата добавления: 2018-02-15; просмотров: 3679; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!