Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
Основные понятия и факты связанные с Д.У.
Определение: Обыкновенное дифференциальное уравнение порядка 
―уравнение вида 
в котором 
―независимая переменная, 
―искомая функция, 
―заданная функция.
Кроме обыкновенных дифференциальных уравнений, 
дифференциальное уравнение в частных производных: для функций нескольких переменных. (Для 
―обыкновенная производная).
Дифференциальное уравнение 
-го порядка ― лишь бы была 
(а все остальное может отсутствовать)
Системы дифференциальных уравнений.
Решить: найти все решения (либо доказать, что их нет).
Решение ― объект, который при подстановке обращает уравнение в истинное
Пусть 
―решение дифференциальное уравнение 
: 
.
Определение: Решение дифференциального уравнения получено в квадратурах, если оно выражено через элементарные функции посредством конечного числа арифметических операций, операций образования сложной функции и несобственных интегралов, при этом решение может быть функцией, заданной явно, неявно, параметрически, а неопределенные интегралы могут быть неберущимися.
(обычно решить ― решить в квадратурах)
― разные формы записи
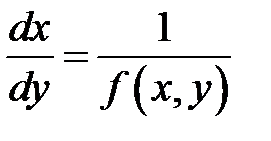. Теперь 
неизвестна.
Для решения в квадратурах менять ролями переменные в дифференциальных уравнениях можно (получается неявная функция)
Определение: Начальное условие для уравнения 
―следующее дополнительное условие для его решения: 
, где 
―заданные числа
|
|
|
Существование, единственность и приближенное решение задачи Коши
Определение: Начальное условие для уравнения ―следующее дополнительное условие для его решения: , где ―заданные числа
Определение: 
и 
―задача Коши (решить дифференциальные уравнения с начальными условиями).
Наиболее типично: у задачи Коши 
единственное решение (но не всегда).
Теорема: Пусть в прямоугольнике 
является непрерывной функцией 
.
Пусть 
, где 
такое дифференциальное уравнение, что 
. Тогда по меньшей мере на отрезке 
единственное решение задачи Коши 
. [Без доказательства]
формулы для приближенного решения задачи Коши (в общем случае точной формулы не существует):
, где 
―такое число, для которого в прямоугольнике П 
.
.
Пример: 
не решается в квадратурах (это доказано)
Задача Коши: 
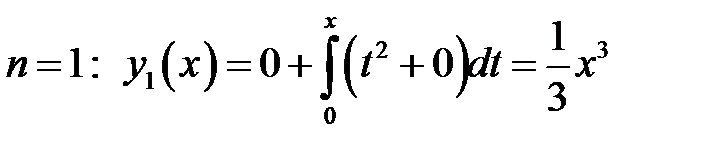
Д.У., описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и д.р.)
Задача о радиоактивном распаде.
―время, 
―масса вещества. 
Задача о гармонических колебаниях
― уравнение 1-го порядка, разрешенное относительно производной
Приближенное построение интегральных кривых с помощью изоклин.
|
|
|
Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
1) уравнение с разделенными переменными:
2) уравнение с разделяющимися переменными:
(следить за пропажей корней)
3) уравнение вида 
―новая функция, зависящая от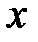 
4) однородное уравнение: 
5) уравнение вида 
.
единственное решение: 
―решение (*)???
.
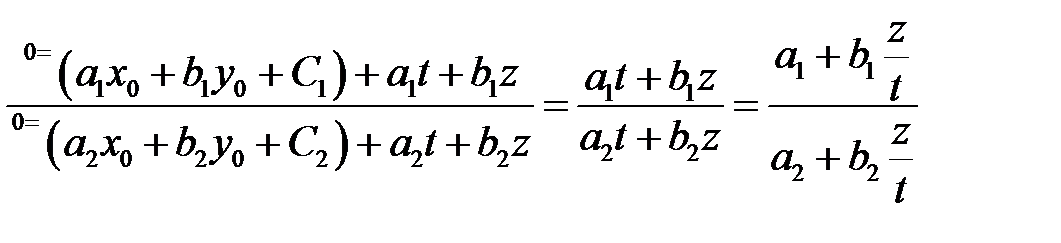
Дата добавления: 2018-02-15; просмотров: 698; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!