Классификация точек разрыва функции
Математическая индукция
Математическая индукция — один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что, если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Бином Ньютона
Бино́мНью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
,
где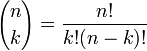 
— биномиальные коэффициенты, 
— неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное рациональное число (возможно, отрицательное). В этом случае бином представляет собой бесконечный ряд
Треугольник Паскаля
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Имеет применение в теории вероятностей.
Последовательность
Последовательность — это набор элементов некоторого множества:
|
|
|
· для каждого натурального числа можно указать элемент данного множества;
· это число является номером элемента и обозначает позицию данного элемента в последовательности;
· для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма.
Предел последовательности
В математике пределом последовательности элементов метрического пространства или топологического пространства называют элемент того же пространства, который обладает свойством «притягивать» элементы заданной последовательности. Пределом последовательности элементов топологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера. В метрическом пространстве окрестности определяются через функцию расстояния, поэтому понятие предела формулируется на языке расстояний. Исторически первым было понятие предела числовой последовательности, возникающее в математическом анализе, где оно служит основанием для системы приближений и широко используется при построениидифференциального и интегрального исчислений.
|
|
|
Непрерывная функция
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Определение 1: Функция f(x) называется непрерывной функцией в точке A, если существует предел данной функции при аргументе стремящимся к A и он равен f(a), т.е. 
.
Критерий непрерывности:
Другими словами, для любого сколь угодно малого числа эпсилон, существует такое число дельта, зависящее от эпсилон, что из того, что для любых иксов удовлетворяющих неравенству следует, что отличия значений функции в данных точках будет сколь угодно мало.
Критерий непрерывности функции в точке:
Функция будет непрерывна в точке A тогда и только тогда, когда она будет непрерывна в точке A и справа и слева, т.е чтобы в точке A существовали два односторонних предела, они были равны между собой и равнялись значению функции в точке A.
Определение 2: Функция непрерывна на множестве, если она непрерывна во всех точках этого множества.
|
|
|
Точки разрыва функции
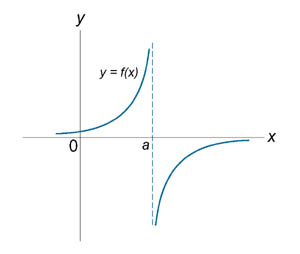
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
Классификация точек разрыва функции Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
При этом возможно следующие два случая:
Такая точка называется точкой устранимого разрыва.
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
| |||||||||||||||||
| Пример 1 | |||||||||||||||||
Исследовать функцию  на непрерывность.
Решение.
Данная функция не определена в точках x = −1 и x = 1. Следовательно, функция имеет разрывы в точкахx = ±1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках.
Поскольку левосторонний предел при x = −1 равен бесконечности, то данная точка является точкой разрыва второго рода.
Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода.
| |||||||||||||||||
и правосторонний предел 
;
называется скачком функции.
Замечательные пределы
Замеча́тельныепреде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известныхматематических тождеств со взятием предела. Особенно известны:
· Первый замечательный предел:
· Второй замечательный предел:
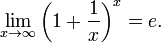
Односторонний предел
Односторо́ннийпреде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́ннимпреде́лом (или преде́ломсле́ва) и правосторо́ннимпреде́лом (преде́ломспра́ва).
Производная
Произво́дная (-ый, -ое) — произведённая, образованная от другой, простейшей или основной величины, формы, категории
Нормаль
Нормаль — это прямая, ортогональная (перпендикулярная) касательному пространству (касательной прямой к кривой, касательной плоскости к поверхности и т. д.).
Великая теорема Ферма
Вели́каятеоре́ма Ферма́ (или Последняя теорема Ферма) — одна из самых популярных теорем математики. Её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Эндрю Уайлсом.
Малая теорема Ферма
Ма́лаятеоре́ма Ферма́ — классическая теорема теории чисел, которая утверждает, что
Если p — простое число, и  не делится на  , то  Другими словами,  при делении нацело на даёт в остатке 1.
|
Равносильная формулировка:
Для любого простого и целого :
 делится на 
|
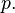
Эту теорему называют малой в отличие от большой теоремы Ферма о невозможности решения в целых положительных числах уравнения 
при целом n>2. Малая теорема Ферма уже давно стала одной из главных теорем для исследований не только в теории целых чисел, но и в более широких областях арифметики и алгебры[1].[2]
Теорема Ролля
Если вещественная функция, непрерывная на отрезке 
и дифференцируемая на интервале 
, принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Теорема Лагранжа
Дата добавления: 2018-02-18; просмотров: 825; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!