Задание на лабораторную работу. Определить устойчивость САУ с помощью критериев Гурвица и Рауса, критический коэффициент усиления и построить переходные характеристики систем управления с
Определить устойчивость САУ с помощью критериев Гурвица и Рауса, критический коэффициент усиления и построить переходные характеристики систем управления с различными значениями k.
Варианты выполнения лабораторной работы приведены в табл. 3.3.
Содержание отчёта по лабораторной работе
o титульный лист;
o цель и задачи работы;
o расчет устойчивости с помощью критериев;
o переходные характеристики;
o выводы.
3.5 Контрольные вопросы:
1. Что такое устойчивость системы?
2. Зачем надо проверять системы на устойчивость?
3. Как определить устойчивость системы по критерию Гурвица?
4. Как определить устойчивость системы по критерию Рауса?
5. Как определить устойчивость системы по переходной характеристике?
6. Как рассчитать критический коэффициент усиления для систем 3 и 4 порядков?
Таблица 3.3
| Варианты | a0 | a1 | a2 | a3 | a4 |
| 1 | 1 | 3 | 5 | 4 | 1 |
| 2 | 4 | 6 | 3 | 1 | |
| 3 | 5 | 8 | 7 | 1 | |
| 2 | 1 | 8 | 6 | 5 | 1 |
| 3 | 4 | 7 | 3 | 1 | |
| 4 | 5 | 9 | 6 | 1 | |
| 3 | 2 | 3 | 5 | 4 | 1 |
| 2 | 7 | 9 | 3 | 1 | |
| 4 | 8 | 8 | 5 | 1 | |
| 4 | 2 | 6 | 8 | 2 | 1 |
| 3 | 5 | 6 | 4 | 1 | |
| 5 | 7 | 7 | 2 | 1 | |
| 5 | 3 | 5 | 7 | 5 | 1 |
| 9 | 6 | 4 | 2 | 1 | |
| 5 | 6 | 7 | 1 | 1 | |
| 6 | 1 | 3 | 5 | 4 | 1 |
| 1 | 8 | 6 | 5 | 1 | |
| 2 | 3 | 5 | 4 | 1 | |
| 7 | 2 | 6 | 8 | 2 | 1 |
| 3 | 5 | 7 | 5 | 1 | |
| 2 | 4 | 6 | 3 | 1 | |
| 8 | 4 | 6 | 7 | 4 | 1 |
| 3 | 4 | 7 | 3 | 1 | |
| 2 | 7 | 9 | 3 | 1 |
Лабораторная работа №4
Исследование устойчивости линейной системы с помощью частотных графоаналитических критериев
|
|
|
Цель работы: изучение методов анализа устойчивости с помощью критериев Михайлова и Найквиста.
Задачи работы: построение годографов Михайлова и Найквиста; определение устойчивости замкнутых систем, критического коэффициента усиления, запаса устойчивости по амплитуде и фазе.
Теоретическое введение
Критерий устойчивости Михайлова
Пусть левая часть характеристического уравнения, называемая характеристическим полиномом, имеет вид

Подставим в этот полином вместо переменного р чисто мнимый корень, который в дальнейшем будем обозначать jw. Тогда получим функцию комплексного переменного

которую можно представить в виде суммы действительной и мнимой частей:
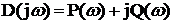
Действительная часть Р (ω) содержит только четные степени переменного ω

а мнимая часть — только нечетные
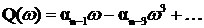
Каждому фиксированному значению переменного ω соответствует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости. Если теперь изменять параметр (ω от 0 до ∞, то конец вектора D (jω) опишет некоторую линию (рис. 4.1, а), которая называется характеристической кривой или годографом Михайлова. По виду этой кривой можно судить об устойчивости системы.
|
|
|
Формулировка критерия Михайлова:
Автоматическая система управления, описываемая уравнением п-го порядка, устойчива, если при изменении с ω от 0 до ∞ характеристический вектор системы D (jω) повернется против часовой стрелки на угол nπ/2, не обращаясь при этом в нуль.
Это означает, что характеристическая кривая устойчивой системы должна при изменении с ω до 0 до ∞ пройти последовательно через п квадрантов. Из приведенных выше выражений следует, что кривая D (jω) всегда начинается в точке на действительной оси, удаленной от начала координат на величину ап.
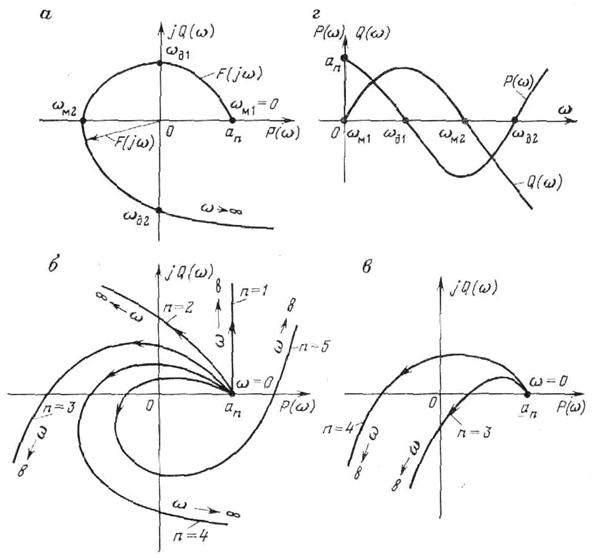
Рис. 4.1 Характеристические кривые (годографы) Михайлова
Характеристические кривые, соответствующие устойчивым системам (рис. 4.1, б), имеют плавную спиралеобразную форму и уходят в бесконечность в том квадранте, номер которого равен порядку уравнения. Если характеристическая кривая проходит п квадрантов не последовательно или проходит меньшее число квадрантов, система неустойчива (рис. 4.1, в).
Если кривая D (jω) проходит через начало координат, то система находится на границе устойчивости. Действительно, если характеристическое уравнение имеет один нулевой корень рk = 0 (апериодическая граница устойчивости) или одну пару чисто мнимых корней рk = ± jβk (колебательная граница устойчивости), то функция D (jω) при ω = 0 или ω = βk обратится в нуль.
|
|
|
Критерий Найквиста
Основная формулировка критерия Найквиста:
Автоматическая система управления устойчива, если амплитудно-фазовая характеристика W (jω) разомкнутого контура не охватывает точку с координатами (— 1; j0).
Эта формулировка справедлива для систем, которые в разомкнутом состоянии устойчивы. Таковыми являются большинство реальных систем, состоящих из устойчивых элементов.
На рис. 4.2изображены амплитудно-фазовые характеристики разомкнутого контура, соответствующие трем различным случаям: система устойчива (кривая 1); система находится на колебательной границе устойчивости (кривая 2); система неустойчива (кривая 3).

Рис. 4.2. Амплитудно-фазовые характеристики разомкнутого контура
Для использования изложенного приема применительно к астатическим системам, которые содержат интегрирующее звено, и амплитудно-фазовые характеристики которых начинаются в – ∞ на мнимой оси, характеристику W (jω) предварительно дополняют в четвертом квадранте дугой окружности бесконечно большого радиуса.
|
|
|
Для суждения об устойчивости систем, имеющих АФХ сложной конфигурации, когда кривая АФХ пересекает действительную ось левее точки (–1; j0) несколько раз, можно также использовать правило переходов, сформулированное советским ученым Я. 3. Цыпкиным: АФХ не охватывает точку (–1; j0), т. е. система устойчива, если при возрастании ω разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФХ через ось абсцисс слева от точки (-1; j0) равна нулю.
Если АФХ начинается или заканчивается на отрезке (- ∞;-1), то считают, что характеристика совершает полперехода.
Частота, при которой амплитудная характеристика А (ω) [модуль функции W (jω)] принимает значение 1, называется частотой среза и обозначается ωср. Частоту, при которой фазовый сдвиг
φ (ω) = - π, обозначают ωπ.
Пользуясь введенными обозначениями, можно записать условие нахождения системы на границе устойчивости:
ωср = ωπ
Частота, с которой система колеблется на границе устойчивости, называется критической и обозначается ωкр.
Таким образом, особая роль точки (-1; j0) заключается в том, что она, во-первых, соответствует превращению отрицательной обратной связи в положительную, и во-вторых, является граничной между режимами усиления и ослабления сигналов звеном W (jω).
Иногда на практике встречаются системы, в контуре которых имеется одно или несколько неустойчивых элементов. Такие системы в разомкнутом состоянии неустойчивы. Для суждения об их устойчивости необходимо использовать другую (обобщенную) формулировку критерия Найквиста:
Автоматическая система управления устойчива, если амплитудно-фазовая характеристика W (jω) разомкнутого контура охватывает l/2 раз точку с координатами (-1; j0), где l – число правых корней характеристического уравнения разомкнутого контура.
Количество охватов при этом можно определять по правилу Цыпкина как разность между числом положительных и отрицательных переходов.
Из обеих формулировок следует, что для суждения об устойчивости системы необходимо предварительно установить устойчивость ее в разомкнутом состоянии. Обычно эта вспомогательная задача решается сравнительно легко, при помощи критерия Гурвица: для этого приравнивают к нулю знаменатель передаточной функции W(р) разомкнутого контура и анализируют данное характеристическое уравнение.
Во многих практических случаях устойчивость разомкнутого контура может быть оценена без каких-либо вычислений непосредственно по виду входящих в контур звеньев.
Запас устойчивости по амплитуде – это расстояние от кривой АФЧХ до точки (-1; 0). Запас устойчивости по фазе – это угол поворота кривой АФЧХ, при котором она будет пересекать точку (-1; 0).
Устойчивость системы управления и запас устойчивости могут быть определены также с использованием пары характеристик: АЧХ и ФЧХ.
Порядок выполнения работы
Критерий Михайлова:
1. Открыть файл MIHAYLOV-1.VSM и задать в нем коэффициенты первой системы К, а0, а1, а2, а3, а4 в соответствии с вариантом.
2. Определить устойчивость замкнутой системы управления с помощью критерия Михайлова (рис. 4.3).

Рис. 4.3. Определение устойчивости по критерию Михайлова
Для выбора наилучшего представления графика можно воспользоваться функцией динамического масштабирования – нажать Ctrl и выделить область, которую нужно увеличить. Для закрепления выбранного масштаба следует щелкнуть правой кнопкой мыши на области построения и отметить галочкой пункт Fixed Bounds.
3. Изменить значение коэффициента К, чтобы система находилась на границе устойчивости.
4. Повторить те же действия (шаги 1-3) для систем №№ 2 и 3.
5. Создать новый файл. Собрать замкнутую систему с единичной обратной связью, задать коэффициенты первой системы в соответствии с вариантом.
6. Определить с помощью критерия Рауса (см. теоретическое введение предыдущей лабораторной работы) устойчивость разомкнутой САУ и число правых корней ее характеристического полинома.
7. Построить (рис. 4.4) АФЧХ (годограф Найквиста), ЛАЧХ и ЛФЧХ для разомкнутой системы (ω = 0.01..100).

Рис. 4.4. Определение устойчивости по критерию Найквиста
8. Определить устойчивость замкнутой системы управления с помощью критерия Найквиста, а также запас устойчивости по амплитуде и фазе.
9. Изменить значение коэффициента К, чтобы система находилась на границе устойчивости.
10. Повторить те же действия (шаги 5-9) для систем №№ 2-5.
Дата добавления: 2018-02-18; просмотров: 1483; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
