Задание на лабораторную работу. Определение частотных характеристик следующих звеньев:
Определение частотных характеристик следующих звеньев:
· Апериодическое звено (I порядка):
 ,
,  ,
,  .
.
· Колебательная система:
 ,
,  ,
,
 ,
,  .
.
· Система управления, состоящая из двух апериодических звеньев:
 ,
, 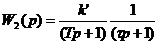 ,
,
 ,
, 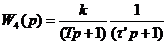 .
.
· Система управления, состоящая из апериодического и колебательного звеньев:
 ,
,  ,
,
 ,
,  .
.
Варианты для выполнения лабораторной работы:
| № варианта | K | K' | T | T' | τ | τ' | d | d' |
| 1 | 10 | 1 | 10 | 100 | 1 | 10 | 0,3 | 0,1 |
| 2 | 1 | 0,1 | 1 | 10 | 10 | 100 | 0,6 | 0,2 |
| 3 | 0,1 | 1 | 1 | 0,1 | 10 | 1 | 0,2 | 0,3 |
| 4 | 1 | 10 | 100 | 10 | 10 | 100 | 0,4 | 0,6 |
| 5 | 0,1 | 0,01 | 0,1 | 0,01 | 1 | 0,1 | 0,1 | 0,2 |
| 6 | 100 | 10 | 0,1 | 1 | 0,01 | 0,1 | 0,3 | 0,6 |
| 7 | 10 | 0,1 | 0,01 | 1 | 1 | 100 | 0,2 | 0,4 |
| 8 | 100 | 1 | 10 | 0,1 | 100 | 1 | 0,1 | 0,2 |
Содержание отчёта по лабораторной работе
o титульный лист;
o цель и задачи работы;
o все полученные графики ЛАЧХ, ЛФЧХ, АФЧХ;
o выводы.
Контрольные вопросы
1. Что такое АЧХ? Что такое ФЧХ?
2. Как влияют праметры апериодического звена на ширину его полосы пропускания?
3. Чему равен фазовый сдвиг (аргумент комплексного коэффициента передачи) апериодического звена на частоте w=1/T ?
4. Как влияют параметры системы на вид ее частотных характеристик?
Лабораторная работа №3
Исследование устойчивости линейной системы с помощью алгебраических критериев
Цель работы: изучение методов анализа устойчивости с помощью критериев Рауса и Гурвица.
Задачи работы: построение определителей Гурвица и таблицы Рауса; определение устойчивости систем управления, критического коэффициента усиления; построение временных характеристик устойчивых и неустойчивых систем.
|
|
|
Теоретическое введение
Критерии устойчивости Гурвица
Наиболее распространены в инженерной практике критерии Гурвица и Рауса. Критерий Гурвица был сформулирован и доказан в 1895 г. немецким математиком А. Гурвицем, который разработал свой критерий, решая чисто математическую задачу – задачу исследования устойчивости решений линейного дифференциального уравнения. Гурвиц обратился к этой задаче по просьбе словацкого ученого А. Стодолы, занимавшегося вопросами регулирования турбин. Применительно к задачам теории управления критерий Гурвица можно сформулировать так:
Автоматическая система, описываемая характеристическим уравнением

где а0 > 0 устойчива, если положительны все определители ∆1 ,∆2, …, ∆n вида

Если хотя бы один из определителей, называемых определителями Гурвица, отрицателен, то система неустойчива.
Матрицы, по которым вычисляют определители Гурвица, составляют следующим образом: на главной диагонали записывают все коэффициенты характеристического уравнения от а1 до аi (в порядке возрастания индекса), затем в каждом столбце выше диагональных коэффициентов записывают коэффициенты с последовательно возрастающими индексами, а ниже — с последовательно убывающими индексами; на место коэффициентов с индексами большими п или меньшими нуля проставляют нули. При этом каждая i-я матрица получается квадратной размером i × i.
|
|
|
Так как последний столбец главного определителя ∆n содержит всегда только один элемент ап, отличный от нуля, то согласно известному свойству определителей
 .
.
Если главный определитель ∆n = 0, а все остальные определители положительны, то система находится на границе устойчивости. С учетом этого выражения это условие распадается на два
 ,
,  .
.
Условию аn = 0 соответствует один нулевой корень, т. е. апериодическая граница устойчивости, а условию ∆ n-1 = 0 – пара мнимых корней, т. е. колебательная граница устойчивости.
Рассмотрим частные случаи критерия Гурвица для n = 1; 2; 3; 4. Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить следующие условия.
1. Для уравнения первого порядка

условие устойчивости
 ,
,  ,
,
т. е. положительность коэффициентов уравнения является в данном случае и необходимым и достаточным условием. Действительно, при a0 > 0 и а1 > 0 единственный корень уравнения будет отрицательным: р1 = - (a1/a0)<0.
|
|
|
2. Для уравнения второго порядка
 ,
,  ,
,  .
.
Таким образом, и для системы второго порядка необходимое условие устойчивости (положительность коэффициентов) является одновременно и достаточным.
3. Для уравнения третьего порядка

условие устойчивости

и т.д.
Последнее неравенство при а3 > 0 эквивалентно неравенству ∆2>0. Следовательно, для системы третьего порядка, кроме положительности всех коэффициентов, требуется, чтобы ∆3>0. Учитывая выражение для Д2, можно сформулировать мнемоническое правило оценки устойчивости систем третьего порядка:
Произведение средних коэффициентов уравнения должно быть больше произведения крайних.
4. Для уравнения четвертого порядка

кроме положительности всех коэффициентов требуется выполнение условия
 .
.
Нетрудно доказать, что при положительности всех коэффициентов это условие обеспечивает выполнение условия ∆2>0. Таким образом,
Для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель ∆n-1 6ыли положительными.
|
|
|
Критерий Гурвица целесообразно применять для анализа устойчивости систем не выше пятого порядка. При п > 5 вычисление определителей становится громоздким.
Критерий устойчивости Рауса
Этот критерий устойчивости был в 1877 г. предложен английским математиком Э. Раусом в виде некоторого правила (алгоритма), которое наиболее просто поясняется табл. 3.1
Таблица 3.1
| C00=a0 | C01=a2 | C02=a4 | C03=a6 | … | |
| C10=a1 | C11=a3 | C12=a5 | C13=a7 | … | |

| 
| 
| 
| … | … |
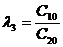
| 
| 
| 
| … | … |

| 
| 
| 
| … | … |

| 
| 
| 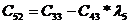
| … | … |
| … | … | … | … | … | … |
| … | … | … | … | … | … |
В первой строке табл. 3.1 записывают в порядке возрастания индексов коэффициенты характеристического уравнения (3.1), имеющие четный индекс; во второй строке — коэффициенты (3.1) с нечетным индексом. Любой из остальных коэффициентов таблицы определяют как
 ,
, 
В выражениях: j — индекс, означающий номер столбца табл. 3.1; i —индекс, означающий номер строки табл. 3.1.
Заметим, что число строк таблиц Рауса равно степени характеристического уравнения плюс единица.
После того как таблица Рауса заполнена, по ней можно сделать суждение об устойчивости системы. Условие устойчивости Рауса формулируется так: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т. е. 
Если не все коэффициенты первого столбца положительны, то система неустойчива, а число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.
Порядок выполнения работы
Критерий Гурвица
Открыть Microsoft Excel в новом документе в верхней строчке ввести название коэффициентов системы a0p4+a1p3+a2p2+a3p+a4+k. Ниже ввести сами коэффициенты (a0= 2, a1= 8, a2= 7, a3= 6, a4= 3, k = 0). Затем на свободном месте написать определитель Гурвица (рис 3.1).


Рис 3.1
Ниже организовать расчет определителей Δ1, Δ2, Δ3, Δ4:
Δ1=a1,
Δ2=a1*a2-a0*a3,
Δ3=a1*a2*a3+a0*a1*0+a3*(a4+k)*0-0*a2*0-a1*(a4+k)*a1-a3*a0*a3
Δ4=a4* Δ3
Можно также воспользоваться МОПРЕД() – стандартной функцией Microsoft Excel.
Критерий Рауса
В свободных ячейках написать таблицу Рауса (рис. 3.2, табл. 3.2):

Рис. 3.2
Таблица 3.2
| C00=a0 | C01=a2 | C02=a4+k | |
| C10=a1 | C11=a3 | ||

| 
| 
| |
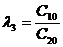
| 
| ||

| 
|
В результате устойчивость разомкнутой САУ будет определена двумя способами (результаты должны совпасть).
Устойчивость замкнутой (с единичной отрицательной обратной связью) зависит от значения статического коэффициента усиления. Требуется подобрать такой коэффициент k=kкр, чтобы замкнутая система оказалась на границе устойчивости (рис. 3.3).

Рис 3.3.
Построим переходную характеристику для системы управления. Собираем схему системы без обратной связи при k равном kкр (граница устойчивости) и системы с единичной обратной связью и коэффициентами усиления, равным kкр, немного (на 10-20%) большим kкр, немного (на 10-20%) меньшим kкр, чтобы среди систем были устойчивая, не устойчивая и лежащая на границе устойчивости (рис 3.4.)

Рис 3.4.
Дата добавления: 2018-02-18; просмотров: 901; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
