Интуитивные методы прогнозирования

Прогнозирование требований абонентов

Введение

Одна из причин качественного развития сети – заинтересованность группы пользователей, приносящей Оператору существенные доходы, в новых видах услуг. Ряд требований этой группы пользователей стимулирует радикальные изменения в различных компонентах телекоммуникационной сети. В настоящее время самые существенные изменения происходят в сетях доступа. Желательно, чтобы качественные изменения были выявлены при разработке прогнозов, которые необходимы для выбора рациональных принципов дальнейшего развития инфокоммуникационной системы.

В процессе планирования телекоммуникационных сетей используются различные методы. Выбор метода осуществляется с учетом поставленной задачи, характера рассматриваемого процесса и доступной статистический информации.

Оценки пропускной способности сети важны для оптимального выбора проектных решений, касающихся транспортных ресурсов и типа коммутационного оборудования. Исходные данные для таких оценок могут быть получены только на основе прогнозов трафика. Этот трафик, в свою очередь, может быть рассчитан, если известны прогнозы, связанные с перечнем поддерживаемых услуг. Важную роль играют показатели качества обслуживания для перспективной телекоммуникационной сети. Например, часть абонентов заинтересована в радикальном улучшении надежности связи, что приводит к резервированию основных элементов сети.

Для пропускной способности сети, перечня поддерживаемых ею услуг и показателей качества обслуживания очень важно – с практической точки зрения – получить два вида прогностических оценок. Во-первых, Оператор должен знать краткосрочный прогноз на ближайшие годы. Во-вторых, для разработки разумной технической политики Оператору необходим также и долгосрочный прогноз на десять-пятнадцать лет, то есть на период срока службы сложных видов телекоммуникационного оборудования.

В процессе планирования телефонной сети важными прогностическими оценками считаются численность потенциальных абонентов и параметры нагрузки. Знание этих данных плюс многолетний опыт эксплуатации ТФОП упрощает решение большинства задач прогнозирования. Для NGN задачи прогнозирования существенно усложняются. Достаточно привести пример с пользователями Internet. Для проектирования сети важно знать не только численность пользователей Internet, но и их распределение с точки зрения используемых транспортных ресурсов. Если пользователь обращается в Internet с помощью оборудования xDSL, то результаты расчета транспортных ресурсов заметно отличаются от оценок, полученных для доступа через модем.

Прогнозирование обычно выполняется для телекоммуникационной системы в целом, а для конкретной задачи используется лишь часть полученных результатов. Задачи прогнозирования целесообразно рассматривать в полном объеме, то есть с точки зрения проектирования, построения, эксплуатации и развития инфокоммуникационной системы.

Формализованные методы прогнозирования

Формализованные методы прогнозирования эффективны в тех случаях, когда хорошо известна предыстория исследуемого процесса. В настоящее время большинство прогнозов осуществляется с помощью методов экстраполяции и экспертных оценок. Каждый из этих двух методов реализуется различными способами, выбор которых зависит от исследуемого процесса и поставленной задачи.

Пример прогнозирования двух процессов, представленных функциями и , показан на рисунке 11.1. Предполагается, что статистические данные, накопленные за период времени , позволяют определить аналитические выражения для функций и . Статистические данные отображены в виде квадратиков на отрезке .

Рис. 11.1. Два примера экстраполяции трендов

Поставленная задача сводится к вычислению значения этих функций для периода прогнозирования – . Соответствующие тренды изображены пунктирными линиями. Кроме того, целесообразно оценить доверительные интервалы. На рисунке 11.1 они показаны для функции штрихпунктирными линиями.

Усложнение разработки прогнозов – помимо проблем с достоверностью необходимой статистической информации – объясняется обстоятельствами такого рода:

некоторые виды новых услуг столь специфичны, что для их прогнозирования очень сложно подобрать адекватные аналоги;
ряду сегментов инфокоммуникационного рынка (характерный пример – мобильная связь) свойственны процессы развития, которые существенно отличаются от тенденций, тщательно изученных Операторами других стран.

Для прогнозирования некоторых величин целесообразно использовать метод, основанный на учете одного из самых важных экономических показателей – валового внутреннего продукта (ВВП) на душу населения. В ряде работ обоснована оценка спроса на инфокоммуникационные услуги – , которую можно представить в таком виде:

. (11.1)

Величины и – значения ВВП на душу населения для прогнозируемого момента времени и начальной точки на оси "Время". Коэффициент определяет степень влияния роста ВВП на уровень платежеспособного спроса для оцениваемой услуги. Функция – одна из прогностических кривых. Чаще всего эти кривые относятся к образным моделям. Подобные модели хорошо отражают развитие процесса, проходящего три основных этапа: медленный старт, интенсивный рост, фаза насыщения. Характерным примером образной модели служит логистическая кривая, которая часто используется для решения задач прогнозирования.

Набор функций , входящих в формулу (11.1) весьма обширен. В частности, в технической литературе рассматриваются такие зависимости:

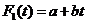. (11.2)

. (11.3)

. (11.4)

. (11.5)

(11.6)

. (11.7)

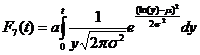. (11.8)

. (11.9)

. (11.10)

Выбор приемлемого тренда часто осуществляется при помощи метода наименьших квадратов. Часто этот метод используется для решения следующей задачи:

для плоскости задано некое множество из 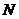точек с координатами ( );
объединение всех точек какой-либо кривой, выраженной в виде известной функции, не представляется возможным без погрешностей;
необходимо выбрать такую функцию 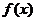, которая обеспечит минимальную погрешность исследуемого процесса.

Метод наименьших квадратов восходит к работам выдающихся математиков К. Гаусса и А. Лежандра. Он предлагает выбирать функцию 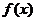, для которой справедливо условие следующего вида:

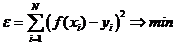. (11.11)

Метод наименьших квадратов часто используется для замены прогностической кривой функцией вида (11.2). Подразумевается, что имеющиеся статистические данные представлены 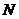значениями величин и 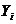. Коэффициенты и определяются такими формулами:

, . (11.12)

Если прогностическая функция существенно отличается от линейной зависимости, формула (11.12) не может быть использована. Тогда параметры прогностической кривой находятся численными методами. В этих случаях также полезен метод наименьших квадратов.

На рисунке 11.2, в качестве примера, показано изменение требований к полосе пропускания в сети доступа для абонентов квартирного сектора в США. Этот прогноз разработан компанией Technology Future Inc. Судя по характеру графиков требования к пропускной способности транспортной сети можно представить суперпозицией функций, каждая из которых очень похожа на логистическую кривую.

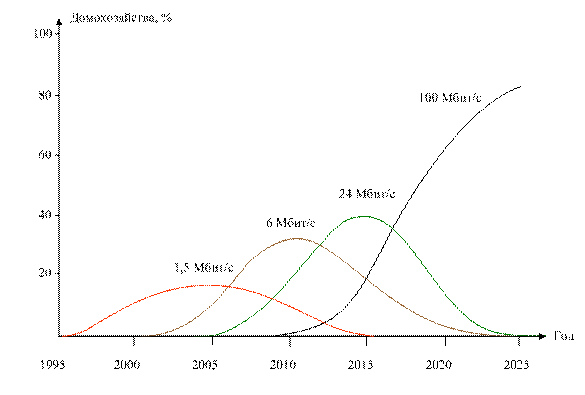
Рис. 11.2. Изменение требований к полосе пропускания сети доступа

Для ряда характеристик инфокоммуникационной системы известна история процесса. Типичный пример – рост емкости ТФОП. В принципе, можно найти статистические данные, относящиеся к концу XIX века. К сожалению, правила подсчета емкости ТФОП периодически менялись. Например, некоторая часть абонентов корпоративных сетей, для которой выделялись ресурсы нумерации ТФОП, иногда приплюсовывалась к общему числу абонентов. В ряде случаев емкость ТФОП вычислялась с учетом АЛ, используемых для таксофонов. Поэтому опубликованные статистические данные можно представить в виде гистограммы, каждый отсчет которой в год представляет собой истинное значение емкости ТФОП 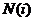с некоторой ошибкой . Функцию 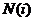можно рассматривать как тренд процесса развития ТФОП. Тогда целесообразно считать случайной ошибкой. Величина этой ошибки, как правило, не зависит от .

Наличие подобной информации о функции 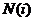позволяет эффективно использовать формализованные методы прогнозирования. Среди этих методов можно выделить экстраполяцию тенденций. На рисунке 11.3 показана гистограмма 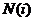, определенная для пяти лет – множество . Предполагается, что все значения 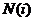достоверны.

Рис. 11.3. Прогнозирование будущего и прошлого

Исследуемый процесс можно также представить непрерывной кривой 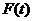. Обычно эта кривая определяется для любого момента времени , лежащего в границах рассматриваемого интервала по оси абсцисс. Поэтому можно говорить об аппроксимирующей кривой вида 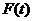. В точках разница между функциям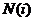и и 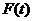представляет собой ошибку аппроксимации – .

Допустим, что необходимо разработать прогноз развития исследуемого процесса для следующих пяти лет. Предполагается, что дальнейшее развитие процесса 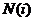– с высокой вероятностью – определяется тем же законом. Это означает, что функция 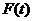в точках будет с приемлемой точностью определять искомые значения .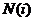

Очевидно, что точность определения величин 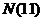… в значительной мере зависит от типа кривой 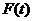. Выбор этой кривой осуществляется с учетом двух факторов. Во-первых, поведение функции 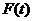должно соответствовать природе исследуемого процесса. Во-вторых, величина ошибки, которая обусловлена заменой функции 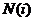, должна быть минимальной.

Для рассматриваемого примера в качестве функции 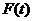можно выбрать полином пятой степени, что обеспечит точное совпадение со статистическими данными в точках при . Очевидно, что такой подход будет противоречить природе исследуемого процесса: ошибки в расчете функци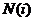и при могут быть очень существенными. При выборе непрерывной кривой, предназначенной для прогнозирования, используются дополнительные приемы. Один из них – "Прогнозирование прошлого".

Словосочетание "прогнозирование прошлого" чаще всего ассоциируется с ретроникой. Здесь этот термин используется для анализа процессов, которые не относятся к истории или к философии. Множество содержит тот набор данных, который используется для прогнозирования на перспективу. Множество включает ретроспективный набор данных, которые не нужны для прогнозирования на перспективу, то есть для определения множества .

Суть "прогнозирования прошлого" заключается в реализации алгоритма, который может быть представлен такой последовательностью операций:

анализ множества позволяет выделить тенденцию, которая может быть экстраполирована на перспективу за счет выбора функции 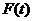методом наименьших квадратов или иным способом;
функция 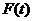используется для расчета значений исследуемого процесса на множестве ;
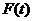если выбранная аппроксимация хорошо совпадает с реальными данными для множества , то выбор функции считается удачным, и она далее используется для решения прогностических задач – для множества ;
если выбранная аппроксимация не совпадает с анализируемым процессом для множества , то следует провести дополнительные исследования для выбора подходящей функции .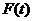

"Прогнозирование прошлого" позволяет решить ряд важных задач. В частности, можно оценить статистические данные за прошедшие годы, если они не собирались или недоступны. Если такие данные имеются, то можно проверить точность результатов "прогнозирования прошлого". При хорошем совпадении результатов прогнозирования и статистики можно утверждать, что предлагаемый метод оценки исследуемой величины выбран удачно.

Интуитивные методы прогнозирования

Для повышения достоверности предсказания исследуемой величины целесообразно использовать несколько методов прогноза. Практически во всех случаях эффективен метод экспертных оценок. В последние годы широкое распространение для решения задач прогнозирования получил метод Делфи (Delphi Method). Коллективное обсуждение проблем часто искажается из-за того, что некоторые эксперты, участвующие в дискуссии, невольно оказывают влияние на аудиторию. Метод Делфи основан на полном отказе от коллективной дискуссии, что исключает влияние таких психологических факторов как согласие с позицией более активных либо авторитетных коллег или желание присоединиться к мнению большинства. Это преимущество достигается за счет роста времени получения результатов.

Раздельная обработка результатов, полученных от двух групп экспертов, означает следующее:

для каждой группы экспертов с помощью известных методов математической статистики устанавливается близость ответов;
в результате формируются два варианта ответа на вопрос, сформулированный перед каждой группой экспертов;
затем с помощью методов математической статистики или иным способом устанавливается близость двух усредненных ответов;
если степень совпадения усредненных ответов приемлема с точки зрения организатора опроса, то задачу прогнозирования можно считать решенной (в противном случае нужны дополнительные исследования).

Следует выделить новые методы, которые могут быть успешно использованы для прогнозирования. Один из таких методов – использование фильтра Калмана. Этот фильтр представляет собой рекурсивное устройство оценки. Алгоритм работы такого устройства позволяет корректировать полученный результат за счет анализа каждой новой выборки, определенной на оси "Время". Другой метод базируется на нейронных сетях. Их построение и анализ в последние годы эффективно используются для решения ряда задач.

Фильтр Калмана не столь эффективен для прогнозов, касающихся, например, потенциального рынка новейших услуг и технологий. Областью эффективного применения калмановской фильтрации, по всей видимости, можно считать сравнительно длительные процессы, меняющие свой характер в некоторых точках на оси "Время". В частности, фильтр Калмана помогает обнаружить точки перегиба образных кривых. Фильтр Калмана целесообразно использовать в качестве дополнения к другим методам прогнозирования характеристик инфокоммуникационных сетей. На практике, если нет необходимости принимать решение в течение небольшого отрезка времени, вместо фильтра Калмана можно использовать результаты периодического мониторинга исследуемого процесса. Цель этого мониторинга – фиксация изменения тренда.

Интуитивные методы прогнозирования полезны при изменении характера исследуемого процесса. Существенные ошибки прогнозирования возникают в тех случаях, когда исследуемый процесс имеет точку перегиба. Характерный пример такого процесса – спрос на услуги телеграфной связи. В середине XX века продолжался рост трафика в сетях телеграфной связи. Затем наступил устойчивый спад спроса на все услуги, которые связаны с телеграфией. Если воспользоваться статистическими данными конца семидесятых годов, то долгосрочный прогноз предусматривал бы рост телеграфного трафика в XXI веке. Этот пример свидетельствует об опасности "слепой" экстраполяции тенденций.

Дата добавления: 2018-02-15; просмотров: 558; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!