Декартово произведение множеств, его свойства. Понятие кортежа. Примеры заданий из начального курса математики, связанных с образованием декартова произведения множеств.
Декартово произведение множеств.
В начальных классах ученики решают задачу: используя цифры 1,2,3 образовать всевозможные двузначные числа.
Путем перебора дети получают
11 12 13
21 22 23
31 32 33
Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.
В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные пары (a;b) образованные из элементов a и b. Это (1;2), (1;3), (1;4) и тд. Первый элемент аназывают первой координатой пары, элемент b – второй.
Значит в нашей задаче мы оперировали множеством A={1,2,3} и образовали всевозможные пары.
Рассмотрим другой пример. Пусть А={1,2,3}, B={4,5}. Образуем всевозможные пары (a;b) так, что a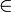 
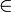A, b B. Получим некоторое новое множество { (1;5), (1;4), (2;4), (2;5), (3;4), (3;5)}, элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств A и B.
Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают А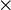 
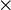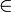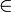В. Таким образом А В ={(х;у) |х А, у В}
Операцию нахождения декартового произведения множеств А и В называют декартовым умножениемэтих множеств.
Рассмотрим следующий пример. Известно, что А 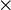В= {(2;3),(2;5), (2;6), (3;3), (3;5), (3;6)}.Установим, из каких элементов состоят множества А и В. Так как первая компонента пары декартового произведения принадлежит множеству А, вторая множеству В, то данные множества имеют следующий вид А={2,3}, В={3,5,6}.
Перечислим элементы принадлежащие множеству А 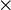В, если А={a,b,c,d}, В=А. Декартово произведение А 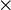В={(a,a), (a,b), (a,c), (a,d), (b,a), (b,b), (b,c), (b,d), (c,a), (c,b), (c,c), (c,d), (d,a), (d,b), (d,c), (d,d)}
|
|
|
Количество пар в декартовом произведении А 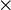В будет равно произведению числа элементов множества А и числа элементов множества В: n(A 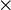B)=n(A) 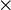n(B).
В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и тд. элементов.
Такие упорядоченные наборы называют кортежами.Так, набор (1,5,6) есть кортеж длины 3, т.к в нем три элемента. Используя понятие кортежа, можно определить понятие декартового произведения n множеств.
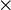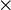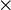Декартовым произведением множеств А1, А2….Аn называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А1, вторая А2, n-ая множеству А: А1 А2 …. Аn.
Пусть даны множества А1 ={2,3} ; А2={3,4,5}; А3={7,8}. Декартово произведение А1 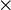А2 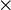А3 ={(2,3,7), (2,3,8), (2,4,7), (2,4,8),(2,5,7),(2,5,8),(3,3,7),(3,4,7),(3,3,8),(3,4,8),(3,5,7),(3,5,8)}
Примеры из начального курса математики.
Например: построй четырехугольник ABCD по координатам его вершин. Если возможно, проведи его оси симметрии. А(0;1), В(2;5), С(6;5) и D(8;1).
|
|
|
Для изображения декартового произведения нечисловых множеств используется таблица. Например: «Фабрика верхнего трикотажа изготавливает мужские пуловеры, женские костюмы, кофты, платья следующих расцветок: бордовая, синяя, голубая,зеленая, коричневая, серая. Составьте таблицу, иллюстрирующую каких цветов могут быть данные изделия».
5.Особенности математический понятий. Объем и содержание понятий. Отношение между понятиями. Остенсивные и контекстуальные определения понятий, их отличие от определений через род и видовое отличие.
Термин понятие соединяет в себе целый класс объектов или отношений произвольной природы, обладающий определенным характеристическим свойством или целым набором таких свойств.
Например понятие четырехугольник обозначает класс всевозможных многоугольников, обладающих свойствами: иметь четыре стороны; иметь четыре вершины; иметь; иметь четыре угла. Понятия условимся обозначать строчными буквами латинского алфавита: a b c
Понятия, изучаемые в начальном курсе математики, представляют в виде четырех групп:
Понятия, связанные с числами и операциями над ними: число, сложение, слагаемое, меньше и др.
|
|
|
Выражение, равенство, уравнение
Геометрические понятия: прямая, отрезок, треугольник
Понятия, связанные с величинами и их измерениями.
Особенности математических понятий: 1)математические объекты, о которых необходимо составить понятия, в реальности не существуют, а существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык
2)в математике рассматриваются не только понятия, появившиеся при изучении реальных предметов, но и понятия, возникшие на основе первых ( например, понятие переменной является абстракцией конкретных переменных величин, т.е. абстракцией от абстракции).
Объем и содержание понятия.
Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла и др. Различают свойства существенные и несущественные.
Существенное свойство- свойство, без которого объект не может существовать.
Несущественное свойство- свойство, отсутствие которого не влияет на существование объекта.
Совокупность всех существенных свойств объекта называют содержанием понятия.
Когда говорят о математическом объекте, имеют в виду всю совокупность объектов, обозначаемых одним термином.
|
|
|
Совокупность всех объектов, обозначенное одним термином, составляет объем понятия.
Например, содержание понятия «квадрат»- это совокупность всех существенных свойств, которыми обладают квадраты, а в объем этого понятия входят квадраты различных размеров.
Итак, любое понятие характеризуется:
-термином( название)
-объемом( совокупность всех объектов, называемых этим термином)
-содержанием( совокупность всех существенных свойств объектов, входящих в объем понятия).
Между объектом понятия и его содержанием существует связь: чем «больше» объем понятия, тем « меньше» его содержание, и наоборот. Объем понятия « треугольник» « больше», чем объем понятия « прямоугольный треугольник», так как все объекты второго понятия являются и объектами первого понятия. Содержание понятия «треугольник» « меньше», чем содержание понятия «прямоугольный треугольник», так как прямоугольный треугольник обладает всеми свойствами любого треугольника и еще другими свойствами, присущими только ему.
Отношения между понятиями.
Определив объем понятия, можно рассмотреть, какие отношения могут существовать между различными их типами.
Отношение эквивалентности существует тогда и только тогда, когда объемы сравниваемых понятий полностью совпадают. Это означает, что отличительные и существенные признаки, присущие сравниваемым понятиям, принадлежат всем элементам множеств, составляющих их объемы. Так, понятия эквивалентности характеризует отношение между классами равносторонних и равноугольных треугольников, равноугольных ромбов и квадратов, понятий, все они принадлежат к одному классу элементов, т.е. имеют тот же самый объем. Обратите внимание на то, что все перечисленные понятия оказываются эквивалентными только по объему, содержание же их различию. Так, признаки « иметь равные стороны» или « обладать равными углами» отличаются друг от друга по смыслу.
Отношение перекрещивания (частичного совпадения) объемов понятий существует тогда и только тогда, когда часть объема одного понятия входит в объем другого, и в свою очередь часть объема второго понятия входит в объем первого. Таковы отношения между объемами понятий «студенты» и «спортсмены», «студенты» и «филателисты», ибо ясно, что не все студенты являются спортсменами или филателистами. Обычно для наглядного изображения отношений между объемами понятий употребляются диаграммы Эйлера, в которых объем понятий представляются кругом. Поскольку у эквивалентных понятий объемы совпадают, то отношение между ними изображается одним кругом. В случае частичного совпадения объемов отношение изображается пересечением двух кругов. Если обозначить объем одного понятия через A , другого через В, то графически отношения эквивалентности (Рис.1) и перекрещивания (Рис.2) можно представить соответствующими диаграммами.
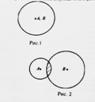
Отношение субординации (подчинение объемов) понятий существует тогда и только тогда, когда объем одного понятия полностью входит в объем второго. Понятие меньше объема составляет часть, или, точнее, вид понятия с большим объемом, который по отношению к нему называют родом. На диаграмме Эйлера (рис.3) это отношение изображается включением меньшего круга в больший.
Все перечисленные выше отношения имеют место между совместными понятиями, объемы которых либо совпадают, либо перекрещиваются, либо составляют часть другого.
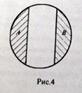
Несравнимые («неположенные») понятия – это понятия, объемы которых либо полностью исключают друг друга, либо находятся в отношении противоречия друг другу . Так объемы понятий «треугольник» и «растение» не содержит ни одного общего элемента, их пересечение – пусто. То же самое можно сказать о понятиях которые употребляются в хорошо известном утверждении, характеризующем несравнимость: «в огороде бузина, а в Киеве дядька». Особый интерес представляют понятия, объемы которых находится в отношении контрарности (противности) друг другу, как, например, «белый» и «черный», «холодный» и «горячий» «длинный» «короткий» и т.д, которые представляют собой свойства, расположенный на границе соответствующих множеств, свойств. Между «белым» и «черным» «холодным» и «горячим» и т.д располагаются промежуточные свойства. В силу этого объемы контрарных понятий занимают крайние положения на круговых диаграммах (рис.4).
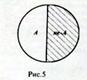
Отношение контрадикторности (противоречивость) между объемами понятий существует тогда , когда они, с одной стороны, отрицают друг друга, а с другой стороны исчерпывают объем целого понятия (рис.5).
В языке противоречий выражается отрицательной частицей перед словом, выражающем свойство. Примерами могут служить свойства, выражающие такие понятий, как белый и не белый, холодный не холодный, черный и не черный и т.д. На диаграмме (рис.5) объемы таких понятий составляют две половины круга, хотя гораздо лучше представить объем положительного понятия кругом, а отрицательного – прямоугольником, в который входит этот круг, поскольку противоположное (отрицательное) понятие содержит обычно больше число элементов (рис.6).
Поскольку объемы понятий образуют классы (или множества) предметов, элементы которых обладают признаками, сформулированными в их содержании, то над этими классами (или множествами) можно производит определенные логические операции. Они тождественны операциям, которые изучаются в теории множеств.
Объединением классов (или множеств) называют класс, который содержит в своём составе те элементы, входящие в каждый отдельный класс. Если обозначить отдельные классы через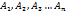 
, то объединенные множества можно представить как дизъюнкцию (или логическое сложение) всех перечисленных классов (или множеств):
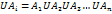
Например, объединение плоских фигур будет состоять из класса треугольников, классы четырехугольников, окружностей и других фигур, класс деревьев – из классов хвойных, лиственных и др. деревьев.
Пересечение (или умножение) классов называется новый класс, который содержит в своём составе те и только те элементы, которые входят в каждый из отдельных классов. Иначе говоря, он содержит элементы, общие всем отдельным классам. Поэтому сама операция пересечения классов иногда называется взятием их общей части. Обозначив отдельные классы через 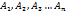, их пересечение можно представить в виде 
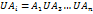, где знак л обозначает операцию пересечения, умножения или конъюнкции классов.
Остенсивные и контекстуальные определения понятий, их отличие от определений через род и видовое отличие.
Контекстуальное (от лат. Contextus-«соединение», «связь») определение характеризуется тем, что она позволяет выяснить суть, значение слова, смысла которого мы не знаем, через контекст, т.е. через относительно законченный отрывок информации, которое сопровождает данное слово, относится к нему и содержит его признаки.
Остенсивное определение устанавливает значение термина, прибегая к демонстрации предмета, обозначаемого этим термином. Такие определения применяются при раскрытии сущности предмета чувственного мира, другими словами, предметов, которые доступны, для непосредственного восприятия.
Дата добавления: 2018-02-18; просмотров: 2789; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!