ІІ етап Всеукраїнської олімпіади з математики 2015 рік. 1. Чи вірно, що для кожного натурального числа n число є простим?
9 клас
1. Чи вірно, що для кожного натурального числа n число є простим? Відповідь обґрунтуйте.
Вказівка:
твердження не вірне, оскільки, наприклад, при n=41 отримуємо - 4341)41(⋅=p cкладене число.
Коментар 1. Якщо встановлено, що p (41) ділиться на 41, і відразу зроблений висновок, що воно складене, то слід знімати 1 бал. Необхідно перевірити, що p (41) не дорівнює 41. Це можна зробити, наприклад, показавши, що воно більше, ніж 41.
Коментар 2. Можливі інші правильні розв’язки, наприклад, можна підставити n=40. Цікаво помітити, що усі числа від p (1) до p (39) - прості.
Відповідь: твердження не вірне.
2. Нехай x і y - додатні дійсні числа. Доведіть, що: .
Вказівка:
Спосіб 1. Піднесемо обидві частини нерівності до квадрату. В силу позитивності обох частин нерівності отримаємо еквівалентну нерівність:
або .
Перенесемо все в ліву частину і зведемо до спільного знаменника:
. А це очевидно, оскільки
Спосіб 2.
Остання нерівність випливає з того, що множники в чисельнику або обидва не негативні (якщо x≥y), або обидва не позитивні (якщо x≤y).
Хоча це випливає також з тотожністі
3. Чи може дискримінант квадратного тричлена з цілими коефіцієнтами дорівнювати 2015?
Вказівка:
Нехай нам даний квадратний тричлен ахbx+с і його дискримінант D=b2b2m+1)m2m+1. Таким чином, дискримінант квадратного тричлена з цілими коефіцієнтами не може дорівнювати 2015. 2+-4ас=2015. Звідси =4ас+2015=4(ас+503)+3, тобто b2 має остачу 3 при діленні на 4. Проте квадрати парних чисел діляться на 4, а квадрати непарних чисел мають остачу 1 при діленні на 4, оскільки (22=4+4
|
|
|
Відповідь: не може.
4. У гострокутному трикутнику АВС проведені висоти AD і СЕ. Точки М і N - основи перпендикулярів, опущених на
пряму DE з точок А і С відповідно. Доведіть, що МЕ = DN.
Вказівка:
Точки D і Е лежать на колі з діаметром АС (див. мал.), значить, ОЕ = ОD, де О - середина сторони АС. Тоді КЕ = КD, де ОКMN. Отже, ОК || АМ, тобто ОК - середня лінія трапеції САМN. Звідси МК = NК, МЕ = DN, оскільки ЕК = КD. ⊥
5. У тридев'ятому царстві є тільки два види монет : 16 і 27 тугриків. Чи можна заплатити за один зошит ціною в 1 тугрик і отримати здачу?
Вказівка:
Можна, наприклад заплатити трьома монетами по 27 тугриків і отримати здачу п'ятьма монетами по 16 тугриків.
Відповідь: можна.
Кожне завдання оцінюється 7-ма балами
Час розв’язання 4 год.
Користування калькуляторами заборонено
ІІ етап Всеукраїнської олімпіади з математики 2015 рік
10 клас
1. Розглядаються квадратичні функції у = х2q у яких р+ q=2015. Доведіть, що їх графіки проходять через одну точку. +рх+
Вказівка:
Розглянемо значення тричлена в точці х+рхq==4+2(р+)=4024, тобто графіки усіх тричленів проходять через точку (2; 4024). 0=2. Тоді 0+qp++24
|
|
|
Відповідь: графіки проходять через точку (2; 4024).
2. Доведіть, що якщо a+b+c = 0 (a ≠ 0), то ab+bc+ca < 0.
Вказівка:
Піднесемо рівність a + b + c = 0 до квадрату. Отримаємо a2b2c2(ab + bc + ca) = 0, тобто ab + bc + ca = - (a2 2 2+++2 + b+ c) < 0.
3. Перша і друга цифри двозначного числа N є відповідно першим і другим членами деякої геометричної прогресії, а саме число N втричі більше третього члена цієї прогресії. Знайдіть усі такі числа N.
Вказівка:
За умовою 10b+bq=3bq2q2q-10=0, q1q2, тобто q=2. З нерівності bq≤9 випливає, що b=1, 2, 3 або 4. , де b≠0 - перший член, q - знаменник геометричної прогресії. Звідси 3-=2, =-
Відповідь: 12, 24, 36, 48.
4. Набір, що складається з чисел a, b, c, замінили на набір a4 b2b4 c2c4 a2– 2, – 2, –2. Набір, що в результаті вийшов, співпав з початковим. Знайдіть числа a, b, c, якщо їх сума дорівнює -3.
Вказівка:
З того, що набори співпадають, слідує збіг їх сум. Значить, a4 -2b2 + b4 -2c2+ c4 – 2a2 = a + b + c = -3, (a2 – 1)+ (b2 – 1)+ (с– 1)= 0, звідки аb2 = ±1, c = ±1 . Умову а + b + с = -3 задовольняють тільки числа а = b = с = - 1. Залишилося перевірити, що знайдена трійка задовольняє умови задачі. 2 2 2 2 2 – 1 = – 1 = с2 – 1 = 0, тобто а = ±1, b
Відповідь: а = b = с = - 1.
5. У трикутнику ABC точки M і N - середини сторін AC і BC відповідно. Відомо, що точка перетину медіан трикутника AMN є точкою перетину висот трикутника ABC. Знайдіть кут ABC.
|
|
|
Т
А
С
B
P
N
H
M
L
K
Вказівка:
Нехай H – точка перетину висот трикутника АВС. За умовою L – середина MN, а . Тому МК=АТ:2=KL. Основа перпендикуляра R з точки М на АР ділить, за теоремою Фалеса, АР пополам, a L є серединою відрізка RP. Тому . Це означає, що R співпадає з H і трикутник MHL є рівнобедреним прямокутним трикутником. Тому і . 1:2:=HLAH2=RLAR045=∠ALM 045=∠ABC
Відповідь: 450.
Кожне завдання оцінюється 7-ма балами
Час розв’язання 4 год.
Користування калькуляторами заборонено
ІІ етап Всеукраїнської олімпіади з математики 2015 рік
11 клас
1. Розв’язати нерівність (х-1)(х2-1)(х3-1)…(х2015-1)≤0.
Вказівка:
Рівняння x[-1;1]. n –1 = 0 має два корені 1 і –1, якщо n – парне; один корінь 1, якщо n – непарне. Застосовуючи метод інтервалів, знаходимо, що х∈
Відповідь: х[-1;1].. ∈
2. Три агрономи, працюючи разом, скопають грядку за 9 хвилин. Грядка також буде скопана, якщо перший пропрацює 5 хвилин, потім другий 15 хвилин, а потім третій 13 хвилин. Скільки хвилин повинен пропрацювати другий агроном, щоб залишити третьому рівно 11 хвилин на завершення скопування, якщо до нього перший пропрацював рівно 7 хвилин? Передбачається, що кожен агроном працює зі своєю позитивною продуктивністю, яка не міняється з часом.
|
|
|
Вказівка:
Позначимо повний об'єм роботи по скопуванню грядки за A. Нехай p1, p2и p3-продуктивності праці відповідно першого, другого і третього агрономів, де продуктивність праці - це об'єм роботи виконуваний за хвилину. Тоді умову задачі можна записати таким чином:
Тут tОскільки p2 - шуканий час роботи другого агронома. Розглянемо півсуми перших двох рівнянь і віднімемо від них третє. Отримаємо 2>0, то робимо висновок, що t2=12. Отже, встановлено, що якщо розв’язання задачі існує, то t2=12.
Це відбувається тому, що в процесі розв’язання, ми робили логічні наслідки, а не здійснювали еквівалентні переходи. Переконаємося, що додатній розв’язок у розглянутої системи існує. Наприклад, можна взяти p1=11A/180, p2=A/45.
Відповідь: 12.
3. Розв’язати рівняння . sin52cos23xx−=
Вказівка:
Рівняння рівносильно системі sin51cos21xx==−. Звідси 52,222,xnnZxkkZππππ=+∈=+∈. Спільними значеннями є . 2,2xllZππ=+∈
Відповідь: . 2,2xllZππ=+∈
4. Дано трикутник ABC. Пряма, паралельна AC, перетинає сторони AB і BC в точках P і T відповідно, а медіану AM - в точці Q. Відомо, що PQ = 3, а QT = 5. Знайдіть довжину AC.
Вказівка:
З подібності трикутників ADM і APQ випливає, що AMAQDM=3, а з подібності трикутників АМС і QMT випливає, що AMQMAC=5. Оскільки DM=AC:2, то
P
A
C
T
D
M
B
Q
3
5
. Тому АС=11. 156=+=+AMQMAMAQACAC
Відповідь: 11.
5. Чи можна в кружечках (див. малюнок) розмістити різні натуральні числа так, щоб суми трьох чисел уздовж кожного відрізка виявилися рівними?
Вказівка:
Нехай необхідне розміщення існує і S - сума усіх розставлених чисел, а числа a і b – це числа, які знаходяться в кружечках, розташованих в яких-небудь двох вершинах трикутника. Тоді для тієї вершини, в якій стоїть число a, сума чисел уздовж трьох відрізків, що містять цю вершину рівна S+2a. Аналогічно, для вершини, в якій стоїть число b, ця сума рівна S+2b. Оскільки суми чисел уздовж будь-якого відрізка рівні, то і суми чисел уздовж трьох відрізків також рівні. Тому S+2a = S+2b, звідки випливає, що a = b. Але це суперечить умові, де сказано, що усі числа мають бути різними. Таким чином, необхідного розташування чисел не існує. Аналогічні міркування можна проводити для будь-якої пари кружечків, через кожний з яких проходить рівно три відрізки.
Відповідь: не можна.
Кожне завдання оцінюється 7-ма балами
Час розв’язання 4 год.
Користування калькуляторами заборонено
Другий етап Всеукраїнської олімпіади юних математиків 2009 р.
Завдання
6 клас
1. Андрійкові було  років
років  місяців тому, а Миколці буде
місяців тому, а Миколці буде  років через
років через  місяців. Хто із них старший за віком? Відповідь обґрунтуйте.
місяців. Хто із них старший за віком? Відповідь обґрунтуйте.
2. Назвемо число «дзеркальним», якщо справа наліво воно читається так само, як і зліва направо. Наприклад, число  – «дзеркальне». Знайдіть усі «дзеркальні» п’ятицифрові натуральні числа, в записі яких використовуються тільки цифри
– «дзеркальне». Знайдіть усі «дзеркальні» п’ятицифрові натуральні числа, в записі яких використовуються тільки цифри  та
та  . Відповідь обґрунтуйте.
. Відповідь обґрунтуйте.
 3. Марійка подивилася на малюнок і сказала: «Тут зображено сім прямокутників: один великий і шість маленьких». «Тут є ще інші – середні прямокутники» – сказала її матір. Скільки ж всього прямокутників на цьому малюнку? Відповідь обґрунтуйте.
3. Марійка подивилася на малюнок і сказала: «Тут зображено сім прямокутників: один великий і шість маленьких». «Тут є ще інші – середні прямокутники» – сказала її матір. Скільки ж всього прямокутників на цьому малюнку? Відповідь обґрунтуйте.
4. Третина військової роти залишилася на території військової частини, а всі інші її бійці поїхали на стрільби. Бійці цієї роти, що залишилися, за обідом з’їли четвертину приготовленого для роти борщу, а бійці, що повернулися зі стрільб, отримали порції борщу в півтора рази більші, ніж видавалися за обідом. Скільки борщу залишилося для ротної собаки Найди? Відповідь обґрунтуйте.
5. Двоє по черзі вписують хрестики в клітинки таблиці розміром  . Програє той, після чийого ходу утвориться квадрат
. Програє той, після чийого ходу утвориться квадрат  , в усіх клітинках якого вписані хрестики. Хто виграє: той хто починає гру чи його суперник, і як потрібно грати, щоб виграти? Відповідь обґрунтувати.
, в усіх клітинках якого вписані хрестики. Хто виграє: той хто починає гру чи його суперник, і як потрібно грати, щоб виграти? Відповідь обґрунтувати.
7 клас
1. Знайдіть  з рівняння
з рівняння 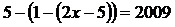 .
.
2. У кімнату з периметром підлоги 22 м поклали килим, краї якого знаходяться на відстані 50 см від кожної стіни. Скільки метрів становить периметр килима?
3.Є  карток, у кожній із яких одна сторона чорна, а друга – біла. Усі ці картки лежать на столі білою стороною догори. Андрійко спочатку перевертає
карток, у кожній із яких одна сторона чорна, а друга – біла. Усі ці картки лежать на столі білою стороною догори. Андрійко спочатку перевертає  карток, потім якісь
карток, потім якісь  карток, а потім якісь
карток, а потім якісь  карток. Чи зможе Андрійко такими діями в кінцевому результаті перевернути усі
карток. Чи зможе Андрійко такими діями в кінцевому результаті перевернути усі  карток чорною стороною догори? Відповідь обґрунтуйте.
карток чорною стороною догори? Відповідь обґрунтуйте.
4. Вздовж дороги довжиною  ростуть лише липи (більше однієї). Перший турист йде по дорозі зі швидкістю
ростуть лише липи (більше однієї). Перший турист йде по дорозі зі швидкістю  . Біля кожної липи він зупиняється і відпочиває одне і те саме ціле число годин. Другий турист їде на велосипеді зі швидкістю
. Біля кожної липи він зупиняється і відпочиває одне і те саме ціле число годин. Другий турист їде на велосипеді зі швидкістю 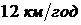 і біля кожної липи відпочиває в двічі довше за першого туриста. Вибули і прибули вони одночасно. Скільки дерев біля дороги? Відповідь обґрунтуйте.
і біля кожної липи відпочиває в двічі довше за першого туриста. Вибули і прибули вони одночасно. Скільки дерев біля дороги? Відповідь обґрунтуйте.
5. Чи можна на дошці розміром  клітинок розташувати декілька тур так, щоб кожна тура била рівно одну іншу туру і при цьому, на кожній вертикалі і на кожній горизонталі повинна бути хоча б одна тура.
клітинок розташувати декілька тур так, щоб кожна тура била рівно одну іншу туру і при цьому, на кожній вертикалі і на кожній горизонталі повинна бути хоча б одна тура.
Відповідь обґрунтуйте. (Тура – це шахова фігура, яка тримає під боєм усі клітинки своєї вертикалі і своєї горизонталі.)
8 клас
1. При яких значеннях  рівняння
рівняння
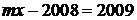 і
і 
мають спільний корінь?
2. Модуль значення виразу  не перевищує 5. Скільки різних цілих значень може набувати значення виразу
не перевищує 5. Скільки різних цілих значень може набувати значення виразу  ?
?
3. Є  карток, у кожної із яких одна сторона чорна, а друга – біла. Усі ці картки лежать на столі білою стороною догори. Петрик спочатку перевертає
карток, у кожної із яких одна сторона чорна, а друга – біла. Усі ці картки лежать на столі білою стороною догори. Петрик спочатку перевертає  карток, потім якісь
карток, потім якісь 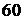 карток, а потім ще якісь
карток, а потім ще якісь  карток. В кінцевому результаті усі
карток. В кінцевому результаті усі  карток виявилися перевернутими чорною стороною догори. Скільки карток були перевернутими три рази? Вкажіть усі можливі відповіді і доведіть, що інших немає.
карток виявилися перевернутими чорною стороною догори. Скільки карток були перевернутими три рази? Вкажіть усі можливі відповіді і доведіть, що інших немає.
4. Іванко і Марічка живуть у висотному будинку, на кожному поверсі якого по  квартир. Номер поверху Іванка дорівнює номеру квартири Марічки, а сума номерів їх квартир дорівнює 239. Який номер квартири, в якій живе Іванко? Відповідь обґрунтуйте.
квартир. Номер поверху Іванка дорівнює номеру квартири Марічки, а сума номерів їх квартир дорівнює 239. Який номер квартири, в якій живе Іванко? Відповідь обґрунтуйте.
5. В п’ятикутній зірці, що зображена на малюнку,  і
і  . Відомо також, що
. Відомо також, що 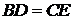 . Доведіть, що
. Доведіть, що  .
.

9 клас
1. Розв’яжіть рівняння 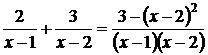 .
.
2. Дано графік лінійної функції  (див. малюнок). Знайдіть значення виразу
(див. малюнок). Знайдіть значення виразу  . Відповідь обґрунтуйте.
. Відповідь обґрунтуйте.

3. Вчителька написала на дошці два натуральних числа. Андрійко помножив перше число на суму цифр другого і отримав
 ,
,
а Миколка помножив друге число на суму цифр першого і отримав
 .
.
 Доведіть, що хтось із них помилився.
Доведіть, що хтось із них помилився.
4. На стороні  трикутника
трикутника  знайшлися точки
знайшлися точки  і
і  такі, що
такі, що  – середина
– середина  і
і 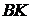 – бісектриса кута
– бісектриса кута  . Крім цього, відомо, що
. Крім цього, відомо, що  . Доведіть, що
. Доведіть, що 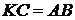 .
.
5. Доведіть, що на дошку розміром  клітинок не можна покласти по клітинках
клітинок не можна покласти по клітинках  доміно (тобто
доміно (тобто  прямокутників
прямокутників  ) так, щоб у кожній горизонталі і у кожній вертикалі вони покривали непарну кількість клітинок. Доміно можуть дотикатися сторонами, але не можуть перекриватися.
) так, щоб у кожній горизонталі і у кожній вертикалі вони покривали непарну кількість клітинок. Доміно можуть дотикатися сторонами, але не можуть перекриватися.
10 клас
1. Графік рівняння  перпендикулярний прямій
перпендикулярний прямій  і проходить через точку з координатами
і проходить через точку з координатами  . Чому дорівнює сума
. Чому дорівнює сума  ?
?
2. Відомо, що число  є коренем рівняння
є коренем рівняння  . Знайдіть значення виразу
. Знайдіть значення виразу  . Відповідь обґрунтувати.
. Відповідь обґрунтувати.
3. Нехай  – сума всіх цифр десяткового запису натурального числа
– сума всіх цифр десяткового запису натурального числа  . Знайдіть усі такі натуральні числа
. Знайдіть усі такі натуральні числа  , для яких
, для яких  . Відповідь обґрунтувати.
. Відповідь обґрунтувати.
 |
4. На продовженні сторони
 вписаного чотирикутника
вписаного чотирикутника  за точку
за точку 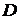 відмітили точку
відмітили точку  так, що
так, що 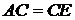 і
і  . Відомо, що
. Відомо, що 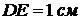 . Знайдіть довжину сторони
. Знайдіть довжину сторони  .
.
5. Доведіть, що для всіх натуральних  справджується нерівність
справджується нерівність
 .
.
11 клас
1. Скільки цілих значень  задовольняють нерівність
задовольняють нерівність
 ?
?
2. Дано куб  з ребром довжини 1. Розглянемо трикутник, одна з вершин якого є точка
з ребром довжини 1. Розглянемо трикутник, одна з вершин якого є точка  , а дві інших лежать на ребрах
, а дві інших лежать на ребрах  і
і  . Знайдіть довжину третьої сторони цього трикутника, якщо відомо, що довжини сторін, які виходять із вершини
. Знайдіть довжину третьої сторони цього трикутника, якщо відомо, що довжини сторін, які виходять із вершини  , дорівнюють
, дорівнюють  та
та  .
.
 3. Знайдіть усі такі дійсні значення
3. Знайдіть усі такі дійсні значення  , при яких числа
, при яких числа  і
і  обидва цілі.
обидва цілі.
4. В трикутнику  з кутом при вершині
з кутом при вершині  , рівним
, рівним  , проведено бісектрису
, проведено бісектрису  . Нехай
. Нехай  – центр вписаного кола трикутника
– центр вписаного кола трикутника  . Описане коло трикутника
. Описане коло трикутника 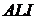 перетинає сторону
перетинає сторону  в точці
в точці 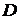 . Доведіть, що точки
. Доведіть, що точки  ,
,  ,
, 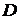 і
і 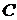 лежать на одному колі.
лежать на одному колі.
5. Нехай  ,
,  і
і  – додатні дійсні числа. Доведіть нерівність
– додатні дійсні числа. Доведіть нерівність
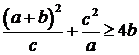 .
.
На виконання роботи виділяється 4 години.
Використання записників і калькулятора не дозволяється.
Другий етап Всеукраїнської олімпіади юних математиків 2009 р.
Відповіді та вказівки
6 клас
6.1. Відповідь. Старший Миколка.
Із умови задачі випливає, що зараз Андрійкові  років і
років і  місяців, а Миколці –
місяців, а Миколці –  років і
років і  місяців.
місяців.
6.2. Відповідь.  ,
,  ,
,  ,
,  .
.
Оскільки першою цифрою будь-якого натурального числа не може бути  , то першою і п’ятою цифрою усіх наших чисел може бути лише
, то першою і п’ятою цифрою усіх наших чисел може бути лише  . Після цього, легко знаходимо два розв’язки, коли посередині «симетричного» числа стоїть
. Після цього, легко знаходимо два розв’язки, коли посередині «симетричного» числа стоїть  , і ще два розв’язки, коли посередині «симетричного» числа стоїть
, і ще два розв’язки, коли посередині «симетричного» числа стоїть  .
.
6.3. Відповідь.  .
.
Крім прямокутників, які назвала Марійка, є ще чотири види прямокутників:
1) два прямокутники виду:
 ;
;
2) чотири прямокутники виду:
 ;
;
3) два прямокутники виду:
 ;
;
4) три прямокутники виду:
 .
.
Всього:  .
.
6.4. Відповідь. Для собаки Найди борщу не залишилося.
На стрільби поїхало  роти, що в двічі більше, ніж залишилося. Якби вони отримали такі самі порції, як бійці за обідом, то вони з’їли б в двічі більше, ніж за обідом, тобто з’їли б половину приготовленого для них усіх борщу. Так як насправді їх порції були в півтора рази більшими, то вони з’їли
роти, що в двічі більше, ніж залишилося. Якби вони отримали такі самі порції, як бійці за обідом, то вони з’їли б в двічі більше, ніж за обідом, тобто з’їли б половину приготовленого для них усіх борщу. Так як насправді їх порції були в півтора рази більшими, то вони з’їли  приготовленого для них усіх борщу. А так як
приготовленого для них усіх борщу. А так як  всього борщу була з’їдена за обідом, то для собаки Найди нічого не залишилося.
всього борщу була з’їдена за обідом, то для собаки Найди нічого не залишилося.
6.5. Відповідь. Виграє другий гравець.
 |
Розділимо дошку на дві рівні частини горизонтальною прямою (див. малюнок).
На кожний хід першого гравця другий повинен відповідати точно таким же ходом, але на другій частині дошки. Наприклад, якщо перший гравець поставив хрестик у лівий верхній кут, то другий гравець повинен поставити хрестик на лівій вертикалі у другу клітинку, рахуючи знизу.
Покажемо, що така стратегія другого гравця призведе його до виграшу. Після кожного ходу другого гравця картинка на обох половинках дошки буде однаковою. Якщо після ходу першого гравця в одній із половинок дошки не утворився квадрат  , заповнений хрестиками, то і після ходу другого в другій половинці дошки такий квадрат утворитися не зможе.
, заповнений хрестиками, то і після ходу другого в другій половинці дошки такий квадрат утворитися не зможе.
Припустимо, що такий квадрат утворився після ходу другого гравця на «стику» двох половинок дошки. Але тоді такий же квадрат утворився раніше, після ходу першого гравця на одній із половинок дошки (див., наприклад, малюнок; останні ходи обох гравців позначені товстим і тонким пунктирним хрестиком відповідно).
Клас
7.1. Відповідь.  .
.
7.2. Відповідь. 18.
7.3. Відповідь. Так, зможе.
Наприклад, наступним чином. Пронумеруємо картки. Нехай Андрійко спочатку перевернув картки  . Потім перевернув картки
. Потім перевернув картки  . І втретє перевернув картки
. І втретє перевернув картки  . В результаті цих трьох дій картки
. В результаті цих трьох дій картки  ,
,  ,
,  ,
,  ,
,  і
і  перевернулися лише один раз, тобто будуть повернутими чорною стороною догори, а картки
перевернулися лише один раз, тобто будуть повернутими чорною стороною догори, а картки  ,
,  ,
,  ,
,  перевернулися три рази, тобто також будуть повернутими чорною стороною догори.
перевернулися три рази, тобто також будуть повернутими чорною стороною догори.
7.4. Відповідь.  дерев.
дерев.
Перший турист знаходився у русі 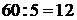 годин, а другий турист
годин, а другий турист  годин. Тому другий турист відпочивав на
годин. Тому другий турист відпочивав на  годин більше першого туриста. Звідси випливає, що перший турист відпочивав рівно
годин більше першого туриста. Звідси випливає, що перший турист відпочивав рівно  годин. Але час відпочинку першого туриста дорівнює добутку числа дерев (лип, їх більше
годин. Але час відпочинку першого туриста дорівнює добутку числа дерев (лип, їх більше  ) на час відпочину біля одного дерева (за умовою це число годин також ціле). Так як
) на час відпочину біля одного дерева (за умовою це число годин також ціле). Так як  – просте число, то це може бути, тільки якщо дерев було
– просте число, то це може бути, тільки якщо дерев було  і турист відпочивав біля кожного дерева рівно
і турист відпочивав біля кожного дерева рівно  .
.
7.5. Відповідь. Так, можна.
Дошка розміром  клітинок розбивається на квадрати
клітинок розбивається на квадрати  клітинки. Потім у кожному квадраті
клітинки. Потім у кожному квадраті  , через який проходить головна діагональ дошки, розташувати фігури так, як це вказано нижче на малюнку, а в усіх інших квадратах фігур не повинно бути. Тоді таке розташування фігур на дошці задовольняє усі умови задачі.
, через який проходить головна діагональ дошки, розташувати фігури так, як це вказано нижче на малюнку, а в усіх інших квадратах фігур не повинно бути. Тоді таке розташування фігур на дошці задовольняє усі умови задачі.

Клас
8.1. Відповідь.  .
.
Легко перевірити, що при  умова задачі не виконується. Якщо
умова задачі не виконується. Якщо  , то коренем першого рівняння буде
, то коренем першого рівняння буде  , а коренем другого рівняння буде
, а коренем другого рівняння буде 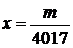 . Отже, для виконання умови задачі необхідно і достатньо, щоб
. Отже, для виконання умови задачі необхідно і достатньо, щоб  . Звідки
. Звідки  . Звідки
. Звідки  .
.
8.2. Відповідь.27.
8.3. Відповідь.  карток були перевернутими три рази.
карток були перевернутими три рази.
Так як усі картки на при кінці виявилися перевернутими, то кожну з них перевертали один або три рази. Всього було зроблено  перевертань:
перевертань:  із них були потрібні для того, щоб перевернути кожну картку один раз; інші
із них були потрібні для того, щоб перевернути кожну картку один раз; інші  перевертань – для того, щоб якісь із карток перевернути ще по два рази. Отже,
перевертань – для того, щоб якісь із карток перевернути ще по два рази. Отже,  карток були перевернуті по три рази.
карток були перевернуті по три рази.
8.4. Відповідь.  .
.
Нехай  – номер квартири Іванка. Тоді, номер його поверху дорівнює
– номер квартири Іванка. Тоді, номер його поверху дорівнює 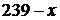 . Частка від ділення з остачею номера квартири на
. Частка від ділення з остачею номера квартири на  дорівнює номеру попереднього поверху, тому:
дорівнює номеру попереднього поверху, тому:  , де
, де  . Звідки знаходимо:
. Звідки знаходимо:  , тобто
, тобто  . Оскільки
. Оскільки  – натуральне число, то
– натуральне число, то  – ціле число. Оскільки
– ціле число. Оскільки  , то
, то 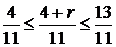 . Звідки випливає, що
. Звідки випливає, що  , а
, а  .
.
 |
8.5. Нехай відрізки
 і
і  перетинають відрізок
перетинають відрізок  у точках
у точках  і
і  відповідно (див. малюнок). Із умови випливає, що трикутники
відповідно (див. малюнок). Із умови випливає, що трикутники  і
і  рівні за стороною і двома прилеглими до неї кутами. З рівності цих трикутників випливає, що
рівні за стороною і двома прилеглими до неї кутами. З рівності цих трикутників випливає, що  і
і  . Тоді
. Тоді  як суміжні до рівних кутів. Одержали, що в трикутнику
як суміжні до рівних кутів. Одержали, що в трикутнику  кути при стороні
кути при стороні  рівні, тобто цей трикутник рівнобедрений. Звідки
рівні, тобто цей трикутник рівнобедрений. Звідки  . Таким чином,
. Таким чином,  , тобто трикутник
, тобто трикутник  – рівнобедрений, з основою
– рівнобедрений, з основою  . Тому,
. Тому,  , що і треба було довести.
, що і треба було довести.
Клас
9.1. Відповідь.  .
.
9.2. Відповідь.  .
.
З малюнку видно, що графік лінійної функції проходить через точки  і
і  . Це означає, що
. Це означає, що  і
і  . Звідки
. Звідки  і
і  . Отже,
. Отже, 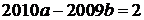 .
.
9.3. Припустимо, що вони обидва не помилилися. Тоді із результату Миколки випливає, що добуток другого числа на суму першого ділиться на  , бо сума цифр числа
, бо сума цифр числа  дорівнює
дорівнює  і ділиться на
і ділиться на  . Звідси випливає, що друге число ділиться на
. Звідси випливає, що друге число ділиться на  , або друге число ділиться на
, або друге число ділиться на  і сума цифр першого ділиться на
і сума цифр першого ділиться на  , або сума цифр першого числа ділиться на
, або сума цифр першого числа ділиться на  . З ознаки подільності на
. З ознаки подільності на  випливає, що сума цифр другого числа ділиться на
випливає, що сума цифр другого числа ділиться на  , або сума цифр другого числа ділиться на
, або сума цифр другого числа ділиться на  і перше число ділиться на
і перше число ділиться на  , або перше число ділиться на
, або перше число ділиться на  . Звідси випливає, що результат Андрійка ділиться на
. Звідси випливає, що результат Андрійка ділиться на  , що неможливо, бо сума цифр числа
, що неможливо, бо сума цифр числа  дорівнює
дорівнює  і на
і на  не ділиться.
не ділиться.
 |
9.4. Нехай
 – середина
– середина  . Тоді
. Тоді  і трикутники
і трикутники  і
і  рівні за двома сторонами і кутом між ними. З рівності цих трикутників випливає, що
рівні за двома сторонами і кутом між ними. З рівності цих трикутників випливає, що  і
і  . Із останньої рівності випливає, що
. Із останньої рівності випливає, що  (як зовнішні до рівних кутів). Тоді трикутники
(як зовнішні до рівних кутів). Тоді трикутники  і
і  рівні за двома сторонами і кутом між ними. Отже,
рівні за двома сторонами і кутом між ними. Отже,  , що і треба було довести.
, що і треба було довести.
9.5. Припустимо, що потрібне розташування доміно вдалося здійснити. Якщо в першій вертикалі доміно займають непарне число клітинок, то хоча б одна клітинка першої вертикалі покрита горизонтальним доміно. Аналогічно хоча б одна клітинка третьої, п’ятої, сьомої, …,  -тої вертикалі покрита хоча б одним горизонтальним доміно. Отже, у нас є не менше
-тої вертикалі покрита хоча б одним горизонтальним доміно. Отже, у нас є не менше  горизонтальних доміно і
горизонтальних доміно і  вертикальних доміно. Тому, всього на дошці є принаймні
вертикальних доміно. Тому, всього на дошці є принаймні  доміно, що суперечить умові задачі (адже нас просять здійснити потрібне розташування доміно за допомогою
доміно, що суперечить умові задачі (адже нас просять здійснити потрібне розташування доміно за допомогою  -ти доміно.
-ти доміно.
Клас
10.1Відповідь.28.
10.2. Відповідь.  .
.
Оскільки  – корінь рівняння
– корінь рівняння  , то
, то  , тобто
, тобто 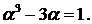 Тому
Тому  . Таким чином,
. Таким чином,

 .
.
10.3. Відповідь.  і
і  . .
. .
Якщо десятковий запис числа  містить не більше трьох цифр, то сума цих цифр не перевищує
містить не більше трьох цифр, то сума цих цифр не перевищує  . Отже,
. Отже,  . Тому,
. Тому,  – чотирицифрове число, перша цифра якого дорівнює
– чотирицифрове число, перша цифра якого дорівнює  або
або  . Якщо перша цифра числа
. Якщо перша цифра числа  дорівнює
дорівнює  , то
, то  і
і  . Нехай
. Нехай 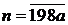 , де
, де  – цифра, тоді
– цифра, тоді  . Звідки
. Звідки  . Нехай
. Нехай 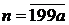 , тоді
, тоді  . Якщо перша цифра числа
. Якщо перша цифра числа  дорівнює
дорівнює  , то перевіривши числа від
, то перевіривши числа від  до
до  , знаходимо ще одне значення
, знаходимо ще одне значення  .
.
10.4. Відповідь.  .
.
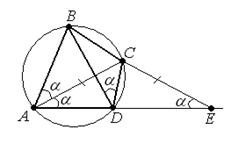 Нехай
Нехай  , тоді
, тоді  як кути при основі рівнобедреного трикутника.
як кути при основі рівнобедреного трикутника.  за умовою задачі;
за умовою задачі; 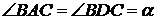 як вписані кути, що спираються на одне і ту саму дугу. Крім того, помічаємо, що
як вписані кути, що спираються на одне і ту саму дугу. Крім того, помічаємо, що  . Тоді трикутники
. Тоді трикутники  і
і  рівні за двома сторонами і кутом між ними. Отже,
рівні за двома сторонами і кутом між ними. Отже,  .
.
10.5. Скористаємося методом математичної індукції.
1) При  одержуємо правильну нерівність:
одержуємо правильну нерівність:  .
.
2) Припустимо, що доводжувана нерівність правильна для  , тобто
, тобто  . Доведемо, використовуючи припущення, що доводжувана нерівність буде правильною і при
. Доведемо, використовуючи припущення, що доводжувана нерівність буде правильною і при  . Дійсно,
. Дійсно,
 ,
,
бо  .
.
Отже, задана нерівність виконується при всіх натуральних  .
.
Клас
11.1. Відповідь.21.
11.2. Відповідь.  .
.
Нехай  і
і  - вершини трикутника. Оскільки
- вершини трикутника. Оскільки  , то
, то 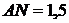 і
і  . За теоремою Піфагора маємо
. За теоремою Піфагора маємо  .
.
11.3. Відповідь. 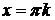 , де
, де  .
.
Нехай  , а
, а  , де
, де  і
і  – цілі числа. Використовуючи формулу для тангенса подвійного аргументу, одержимо:
– цілі числа. Використовуючи формулу для тангенса подвійного аргументу, одержимо:  . Звідки випливає, що
. Звідки випливає, що  . Якщо
. Якщо  , то число
, то число  взаємно просте з числами
взаємно просте з числами  і
і  . Тому, для того щоб число
. Тому, для того щоб число  було цілим, потрібно щоб число
було цілим, потрібно щоб число  було цілим. Звідки випливає, що
було цілим. Звідки випливає, що  або
або 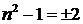 . Отже,
. Отже,  , але тоді і
, але тоді і  . Розв’язавши рівняння
. Розв’язавши рівняння  , знаходимо, що
, знаходимо, що 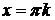 , де
, де  .
.
11.4. Оскільки  – центр вписаного кола трикутника
– центр вписаного кола трикутника  , то прямі
, то прямі  і
і  – бісектриси кутів
– бісектриси кутів 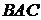 і
і  . Тому,
. Тому,
 .
.
 |
Отже,
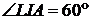 як зовнішній кут трикутника
як зовнішній кут трикутника  . Оскільки точки
. Оскільки точки  ,
,  ,
,  ,
, 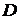 лежать одному колі, то
лежать одному колі, то 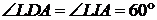 (як вписані кути, що спираються на одну й ту саму дугу). Звідки
(як вписані кути, що спираються на одну й ту саму дугу). Звідки  (як суміжний кут до кута
(як суміжний кут до кута  ). Таким чином,
). Таким чином,  , тобто чотирикутник
, тобто чотирикутник 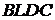 – вписаний, що і треба було довести.
– вписаний, що і треба було довести.
11.5. Розглянемо різницю між лівою і правою частинами даної нерівності і доведемо, що вона невід’ємна. Дійсно,
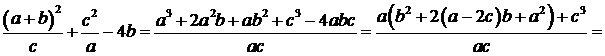





Клас
Дата добавления: 2018-02-18; просмотров: 1385; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
