Властивості операцій над множинами
Лекція 1. Вступні зауваження
План
Множини та їх властивості
Поняття інфімума та супремума множини
Лема про вкладені відрізки
Поняття покриття множини. Лема Бореля
Множини та їх властивості
Поняття множини належить до фундаментальних понять математики, строгого визначення якого не існує до цього моменту. Наслідком цього є наявність парадоксів і протиріч у теорії множин.
Визначення 1 (за Кантором). МножинаS – це будь-яка сукупність визначених об'єктів довільної природи нашої інтуїції або інтелекту, що розрізняються між собою, яка розглядається як єдине ціле. Ці об'єкти будемо називати елементами або членами множини S. Елементи множин позначають малими літерами, самі множини – великими.
Якщо  є (не є) елементом множини
є (не є) елементом множини  , то пишуть:
, то пишуть:
 .
.
Множини можуть складатися з скінченної або нескінченної кількості елементів, тоді вони називаються відповідно скінченними чи нескінченними множинами. Кількість елементів множини  називається її потужністю і позначається
називається її потужністю і позначається  . Для нескінченної множини
. Для нескінченної множини  :
:  .
.
Приклади нескінченних множин.
1. Множина натуральних чисел -  - це числа, які використовуються при рахуванні: 1, 2, 3, ....
- це числа, які використовуються при рахуванні: 1, 2, 3, ....
2. Множина цілих чисел -  - це натуральні числа, їм протилежні і нуль: ....., -2, -1, 0, 1, 2, .....
- це натуральні числа, їм протилежні і нуль: ....., -2, -1, 0, 1, 2, .....
3. Множина раціональних чисел -  - це числа, які представляються у вигляді:
- це числа, які представляються у вигляді:  , де
, де  , чи у вигляді періодичного десятичного дробу. Наприклад,
, чи у вигляді періодичного десятичного дробу. Наприклад,  .
.
|
|
|
4. Множина ірраціональних чисел – це числа, які можуть бути представлені у вигляді неперіодичного десятичного дробу, наприклад,  .
.
5. Множина дійсних чисел -  .
.
Множина повністю визначається своїми елементами: щоб задати множину, потрібно вказати, які елементи їй належать. Це можна зробити різними способами:
· Перерахуванням елементів - у цьому випадку всі елементи беруть у фігурні дужки й розділяють комами (так можуть задаватися тільки скінченні множини). Наприклад,  ;
;
· Характеристичним предикатом – характеристичний предикат – це деяка умова, що дозволяє перевірити, чи належить будь-який даний елемент множині. Якщо для даного елемента умова виконана, то він належить обумовленій множині, а якщо ні, то - не належить. Завдання у вигляді характеристичного предиката виглядає наступним чином: 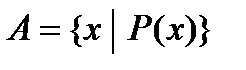 . Наприклад, нехай
. Наприклад, нехай  - це множина парних натуральних чисел, тоді
- це множина парних натуральних чисел, тоді
 .
.
Нехай  - це множина дійсних коренів рівняння
- це множина дійсних коренів рівняння 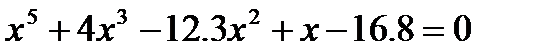 , ця множина скінченна, але її елементи поки що є невідомими. Визначити таку множину теж можно за допомогою визначення властивості її елементів:
, ця множина скінченна, але її елементи поки що є невідомими. Визначити таку множину теж можно за допомогою визначення властивості її елементів:

 .
.
Визначення 2. Множини  і
і  будуть рівними (
будуть рівними (  ), якщо вони складаються з однакових елементів, тобто можна доказати одночасно дві умови:
), якщо вони складаються з однакових елементів, тобто можна доказати одночасно дві умови:
|
|
|
1. Якщо елемент  , то
, то  ;
;
2. Якщо елемент 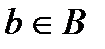 , то
, то  .
.
Визначення 3. Кажуть, що множина  є підмножиною множини
є підмножиною множини  і позначають:
і позначають:
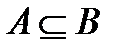 чи
чи 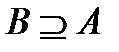 ,
,
якщо кожний елемент множини  є одночасно елементом множини
є одночасно елементом множини  . Якщо множина
. Якщо множина  містить хоча б один елемент, який не належить
містить хоча б один елемент, який не належить  , то
, то 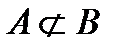 - множина
- множина  не є підмножиною множини
не є підмножиною множини  .
.
Наприклад,  .
.
Приклад. Нехай 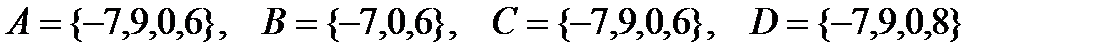 . Тоді:
. Тоді:
 .
.
Елементами множини можуть бути інші множини, наприклад, 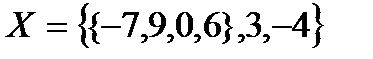 . Множина
. Множина  містить 3 елементи:
містить 3 елементи:  . Зазначимо, що для множини
. Зазначимо, що для множини  :
:  , бо елементи
, бо елементи  - це
- це  , і, наприклад,
, і, наприклад,  .
.
Серед множин існує одна, яка за своїми властивостями і складом принципово відрізняється від всіх інших – це порожня множина, яка не містить в своєму складі жодного елемента і позначається  .
.
Для будь-якої множини  вірно:
вірно:  , оскільки порожня множина не містить таких елементів, які б не належали
, оскільки порожня множина не містить таких елементів, які б не належали  .
.
Для скорочення запису і зручності надалі будемо використовувати два квантори:
 - «будь-який», «для будь-якого»;
- «будь-який», «для будь-якого»;
 - «існує», «знайдеться».
- «існує», «знайдеться».
Властивості підмножин
1. Для будь-якої множини  вона є своєю підмножиною. З використанням введених кванторів ця властивість може бути записано наступним чином:
вона є своєю підмножиною. З використанням введених кванторів ця властивість може бути записано наступним чином:
 .
.
2.  якщо
якщо  , то
, то 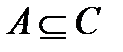 .
.
|
|
|
3. 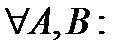 якщо
якщо  , то
, то  . Ця властивість є умовою рівності двох множин.
. Ця властивість є умовою рівності двох множин.
4. 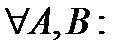 якщо
якщо 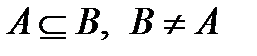 , то
, то  .
.
5. 
 .
.
Необхідно розрізняти відношення включення, тобто відношення «бути підмножиною» (це відношення між множинами) і приналежності (відношення між елементами й множиною). Наведені вище властивості не мають місця для відношення приналежності. Наприклад:  . Звідси не випливає, що
. Звідси не випливає, що  .
.
Будь-яка непорожня множина  має завжди хоча б 2 підмножини:
має завжди хоча б 2 підмножини:  . Якщо
. Якщо  містить
містить  елементів, та кількість різних її підмножин -
елементів, та кількість різних її підмножин -  .
.
Визначення 4. Говорять, що між множинами  і
і 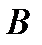 встановлена взаємо-однозначна відповідність, якщо кожному елементу множини
встановлена взаємо-однозначна відповідність, якщо кожному елементу множини  відповідає один і тільки один елемент множини В, і кожному елементу множини В відповідає один елемент множини А.
відповідає один і тільки один елемент множини В, і кожному елементу множини В відповідає один елемент множини А.
Якщо між множинами  і
і 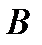 може бути встановлена взаємо-однозначна відповідність, то множини мають однакову потужність і називаються рівнопотужними:
може бути встановлена взаємо-однозначна відповідність, то множини мають однакову потужність і називаються рівнопотужними:  .
.
Приклад. Множина десяткових цифр рівнопотужна множині пальців на руках людини, але не рівнопотужна множині пальців на руках і ногах.
Приклад. Множина парних натуральних чисел рівнопотужна множині всіх натуральних чисел.
Операції над множинами
Об'єднання множин  – це множина
– це множина
 .
.
Визначається однозначно.
|
|
|
Переріз множин  – це множина
– це множина
 .
.
Для будь-яких множин  маємо:
маємо:
 .
.
Дві множини називаються неперетинними, якщо  , і перетинними інакше.
, і перетинними інакше.
Абсолютне доповнення (або просте доповнення) множини А - це
 .
.
Відносне доповнення множини В до множини А (або різниця А-В) – це
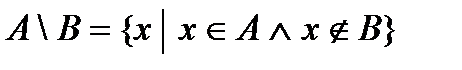 .
.
Симетрична різниця А і В:  .
.
Властивості:
 ;
;
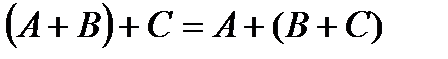 ;
;
 .
.
Властивості операцій над множинами
Теорема 1. Нехай 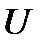 - універсальна множина, тобто множина, яка для конкретної розглянутої задачі включає всі інші множини як підмножини. Для
- універсальна множина, тобто множина, яка для конкретної розглянутої задачі включає всі інші множини як підмножини. Для 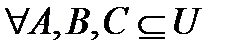 мають місце рівності:
мають місце рівності:
1. Ідемпотентність:
 ;
;  ;
;
2. Комутативність:
 ,
,  ;
;
3. Асоціативність:
 ,
,  ;
;
4. Дистрибутивність:
 ,
,  ;
;
5.  ,
,  ;
;
6.  ,
,  .
.
Властивості множин у теоремі 1 записуються парами. Рівність теорії множин, яка виходить із іншої рівності заміною всіх операцій  на
на  ,
,  на
на  ,
,  на
на  ,
,  на
на  , називається двоїстою до вхідної.
, називається двоїстою до вхідної.
Принцип двоїстості: Якщо в теорії множин можна показати справедливість якогось твердження, то двоїсте твердження також буде мати місце.
З теореми 1 випливає, що об'єднання й переріз множин А,В,С можна записувати без дужок:  ,
,  .
.
Методом математичної індукції можна довести, що об'єднання й переріз будь-якого числа множин можна записувати без дужок, тобто
 ,
,  - загальні асоціативні закони.
- загальні асоціативні закони.
Мають місце загальні комутативні й дистрибутивні закони:
 , де
, де  - будь-яка перестановка чисел
- будь-яка перестановка чисел  ;
;
 .
.
Теорема 2.Нехай 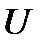 - універсальна множина. Для
- універсальна множина. Для  мають місце рівності (
мають місце рівності (  ):
):
1. Якщо для всіх А  . Якщо для всіх А
. Якщо для всіх А  .
.
2. Якщо  і
і  , то
, то 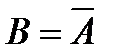 .
.
3.  ;
;
4.  ,
,  ;
;
5. Закони поглинання:
 ,
,  ;
;
6. Закони де-Моргана:
 ,
,  .
.
Теорема 3. Твердження  ,
,  ,
,  еквівалентні для будь-яких множин А и В.
еквівалентні для будь-яких множин А и В.
Дата добавления: 2018-02-18; просмотров: 1250; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
