Уравнение Бернулли. Динамическое давление.
Уравнение Бернулли и следствия из него

Выделим в стационарно текущей идеальной жидкости (физическая абстракция, т. е. воображаемая жидкость, в которой отсутствуют силы внутреннего трения) трубку тока, ограниченную сечениями S1 и S2, по которой слева направо течет жидкость (рис. 47). Пусть в месте сечения S1 скорость течения v1, давление р1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость течения v2, давление р2 и высота сечения h2. За малый промежуток времени Dt жидкость перемещается от сечений S1 и S2 к сечениям S'1 и S'2.
Согласно закону сохранения энергии, изменение полной энергии E2-Е1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы от жидкости: E2-E1=A, (30.1)
где E1 и Е2 — полные энергии жидкости массой m в местах сечений S1 и S2 соответственно.
С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S1 и S2, за рассматриваемый малый промежуток времени Dt. Для перенесения массы т от S1 до S'1 жидкость должна переместиться на расстояние l1= v1Dt и от S2 до S'2 — на расстояние l2= v2Dt. Отметим, что l1 и l2 настолько малы, что всем точкам объемов, закрашенных на рис. 47, приписывают постоянные значения скорости v, давления р и высоты h. Следовательно, A = F1l1+F2l2, (30.2)
где F1=p1S1 и f2=-р2S2 (отрицательна, так как направлена в сторону, противоположную течению жидкости; рис.47).
Полные энергии Е1 и e2 будут складываться из кинетической и потенциальной энергий массы m жидкости:
Подставляя (30.3) и (30.4) в (30.1) и приравнивая (30.1) и (30.2), получим
Согласно уравнению неразрывности для несжимаемой жидкости (29.1), объем, занимаемый жидкостью, остается постоянным, т. е.
Разделив выражение (30.5) на DV, получим
где r — плотность жидкости. Но так как сечения выбирались произвольно, то можем записать
Выражение (30.6) выведено швейцарским физиком Д. Бернулли (1700—1782; опубликовано в 1738 г.) и называется уравнением Бернулли. Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико.
Величина р в формуле (30.6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина rv2/2 — динамическим давлением. Как уже указывалось выше (см. § 28), величина rgh представляет собой гидростатическое давление.
Для горизонтальной трубки тока (h1=h2) выражение (30.6) принимает вид
где р+rv2/2 называется полным давлением.
Вязкость. Движение тел в жидкостях и газах.
Одной из важнейших задач гидро- и аэродинамики является изучение движения твердых тел в газе и жидкости, в частности изучение тех сил, с которыми среда воздействует на движущееся тело. Эта задача стала особенно значимой в связи с бурным развитием авиации и значительным увеличением скорости движения морских судов.
На тело, которое движется в жидкости или газе, действуют две силы (равнодействующую их обозначим R), одна из которых (Rx) направлена в сторону, противоположную движению тела (в сторону потока), - лобовое сопротивление, а вторая (Ry) перпендикулярна этому направлению - подъемная сила
Если тело обладает осью симметрии, которая совпадает с направлением скорости, то на данное действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Доказано, что в идеальной жидкости равномерное движение происходит без лобового сопротивления. Если исследовать движение кругового цилиндра в такой жидкости (рис. 2), то картина линий тока симметрична как относительно прямой, проходящей через точки А и В, так и относительно прямой, проходящей через точки С и D, т. с. результирующая сила давления на поверхность цилиндра будет равна нулю.
Другим образом обстоит дело если происходит движение тела в вязкой жидкости (особенно при увеличении скорости обтекания). Из-за вязкости среды в области движения, прилегающей к поверхности тела, создается пограничный слой частиц, которые движутся с меньшими скоростями. В результате тормозящего действия этого слоя частицы начинают вращаться и движение жидкости в пограничном слое становится вихревым. Если тело не обладает обтекаемой формой (нет плавно утончающейся хвостовой части), то происходит отрыв пограничного слоя жидкости от поверхности тела. При этом за телом возникает течение жидкости (газа), которое направлено противоположно набегающему потоку. Оторвавшийся пограничный слой, следуя за этим течением, образует вихри, вращающиеся в противоположные стороны
Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным коэффициентом сопротивления Cx, который определяется экспериментально:

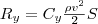 (1)
(1)
где ρ - плотность среды; ν - скорость движения тела; S - наибольшее поперечное сечение тела.
Составляющую Rx можно значительно уменьшить, если подобрать тело формы, не способствующей образованию завихрения.
Подъемная сила может быть определена формулой, аналогичной (1):
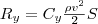
где Cy - безразмерный коэффициент подъемной силы.
Дата добавления: 2018-02-18; просмотров: 1177; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
