Удар абсолютно упругих тел. Удар абсолютно неупругих тел. Диссипация энергии.
Удар абсолютно упругих и неупругих тел является примером применения законов сохранения импульса и энергии при решении физической задачи.
Удар (или соударение) - это столкновение двух или более тел, взаимодействующих очень короткое время. Кроме ударов в прямом смысле этого слова (столкновения атомов или игровых шаров) сюда можно отнести и такие, как столкновение человека с землей при прыжке с парашюта и пр. Силы взаимодействия между сталкивающимися телами столь велики, что мы можем пренебречь прочими внешними силами, действующими на них. Это позволяет приближенно рассматривать систему тел в процессе их соударения как замкнутую и применять к ней законы сохранения.
При ударе тела испытывают деформацию. Понятие удара подрузамевает, что кинетическая энергия относительного движения ударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Опыты показывают, что относительная скорость тел после соударения не достигает своего значения до соударения. Это объясняется тем, что не бывает идеально упругих тел и идеально гладких поверхностей. Отношение нормальной составляющей относительной скорости тел после удара к нормальной составляющей относительной скорости тел до удара называется коэффициентом восстановления ε: ε = νn'/νn
Если для соударяющихся тел ε=0, то такие тела называются абсолютно неупругими, если ε=1 - абсолютно упругими. На практике для всех тел 0<ε<1 (например, для шаров из слоновой кости ε=0,89 ; для стальных шаров ε=0,56, для свинца ε≈0). Но в некоторых случаях тела можно с большой степенью точности рассматривать либо как абсолютно неупругие, либо как абсолютно упругие.
|
|
|
Линией удара называется прямая, проходящая через точку соприкосновения тел и перпендикулярная к поверхности их соприкосновения. Удар называется центральным, если соударяющиеся тела до удара движутся вдоль прямой, проходящей через центры их масс. Здесь мы рассматриваем только центральные абсолютно упругие и абсолютно неупругие удары.
Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай).
ДИССИПАЦИЯ ЭНЕРГИИ (от лат. dissipatio - рассеяние) - переход части энергии упорядоченных процессов (кинетич. энергии движущегося тела, энергии электрич. тока и т. п.) в энергию неупорядоченных процессов, в конечном счёте - в теплоту. Системы, в к-рых энергия упорядоченного движения с течением времени убывает за счёт Д. э., переходя в др. виды энергии, напр. в теплоту или излучение, наз. диссипативными. Для учёта процессов Д. э. в таких системах при определ. условиях может быть введена диссипативная функция. Если Д. э. происходит в замкнутой системе, то энтропия системы возрастает. Д. э. в открытых системах, обусловленная процессами уноса энергии из системы, напр. в виде излучения, может приводить к уменьшению энтропии рассматриваемой системы при увеличении полной энтропии системы и окружающей среды. Это, в частности, обеспечивает важную роль процессов Д. э. в уменьшении уд. энтропии вещества на стадиях образования галактик и звёзд в теории горячей Вселенной. М. Ю. Хлопов
|
|
|
Момент инерции.
Момент инерции - величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело. Момент инерции элементарной (точечной) массы mi, отстоящей от оси на расстоянии ri, равен:
|
|
|
Момент инерции всего тела относительно оси равен:
или, для непрерывно распределенной массы:
Момент инерции всего тела сложной конфигурации обычно определяют экспериментально
Теорема Штейнера.
Вычисление моментов инерции во многих случаях можно упростить, используя соображения симметрии и теорему Штейнера. Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
где
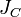— известный момент инерции относительно оси, проходящей через центр масс тела,
— искомый момент инерции относительно параллельной оси,
— масса тела,
— расстояние между указанными осями.
Дата добавления: 2018-02-18; просмотров: 1323; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!