Тригонометрические подстановки

⇐ ПредыдущаяСтр 2 из 2

Интегралы вида 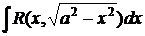, , приводятся от рациональной относительно и функции с помощью тригонометрических подстановок:

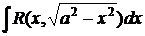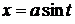- или ;

- или .

6. Интегралы вида

Интеграл данного вида может быть преобразован к интегралу вида , который был рассмотрен в п. 1.9.5.

Произведем преобразования трехчлена, стоящего под корнем:

Сделаем замену переменной, положив 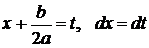. Тогда

Рассмотрим все возможные случаи.

1. Пусть , . Введем обозначения , . В этом случае будем иметь

2. Пусть , . Тогда , . Следовательно,

3. Пусть , . Тогда , . Следовательно,

4. Пусть , . В этом случае есть комплексное число при любом x.

Таким образом, данный интеграл преобразуется к одному из следующих типов интегралов:

, , ,

которые сводятся к интегралам, рассмотренным в п. 1.9.5.

1.10. Функции, интегралы от которых
не выражаются через элементарные функции

В п. 1.1 отмечалось, что всякая функция f(x), непрерывная на интервале (a, b), имеет на этом интервале первообразную, т. е. существует такая функция F(x), что Однако не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции. Таковы первообразные, выраженные интегралами , , , , , и многие другие.

Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций. Так, например, та из первообразных , которая обращается в нуль при x = 0, называется функцией Лапласа и обозначается Ф(х). Таким образом,

, если Ф(0) = 0.

Эта функция хорошо изучена. Составлены подробные таблицы ее значений при различных значениях х.

Та из первообразных , которая обращается в нуль при x = 0, называется эллиптическим интегралом и обозначается Е(х), т. е.

, если Е(0) = 0.

Для этой функции также составлены таблицы значений при различных значениях х.

2. Интеграл по мере области

2.1. Понятие интеграла по мере области

При решении многих задач физики, техники, математики требуется вычислить какие-то суммарные характеристики рассматриваемого объекта или процесса (часто говорят: «интегральные характеристики»). При этом характеристики объекта или процесса могут быть переменными: говорят, что локальные характеристики переменны и зависят от координат, времени. К таким задачам относятся, например, задачи отыскания площади, объема тел различной конфигурации, массы, моментов инерции тел, материал которых имеет различную плотность в различных точках, нахождения пути, пройденного материальной точкой при движении с изменяющейся скоростью, и т. д.

При решении таких задач используется общая математическая модель – интеграл по мере(или «интеграл по фигуре»).

Рассмотрим, как решается задача об отыскании массы тела, плотность которого в каждой точке известна и различна. Этим телом (фигурой) может быть:

1) прямолинейный стержень – l;

2) криволинейный стержень – L;

3) плоская пластина любой формы – D;

4) криволинейная поверхность – G;

5) тело, ограниченное любыми поверхностями, – V.

Чтобы обобщить эти объекты, будем говорить о фигуре G, обладающей некоторой массой. Пусть известна плотность распределения массы этой фигуры в каждой её точке Р

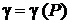Так как масса – величина положительная, то необходимо считать эту функцию непрерывной и положительной на G.

Вычислим массу такой фигуры.

1. Разобьем фигуру G произвольным образом на непересекающиеся части . Заметим, что при таком делении мы используем метрическую характеристику:

- в – длина;

- в – площадь;

- в – объем.

Будем обозначать эту характеристику и назовём её мерой.

Меру можно представить как функцию множества

т. е. множество отображается на множество действительных чисел.

Основные свойства меры:

а) неотрицательность

;

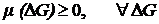б) аддитивность

предполагается, что .

2. В каждой части выберем произвольную точку P_i и предположим, что плотность массы постоянна в пределах и равна её значению в точке P_i, т. е. .

3. Определим приближенное значение массы части

4. Масса (приближение) всей фигуры ищется суммированием частичных масс

Выражение, стоящее справа, называется интегральной суммой.

5. Для нахождения точного значения массы переходим к пределу, устремив к нулю наибольший из диаметров частей . Обозначим его :

Тогда

Заметим, что при .

Если теперь отвлечься от конкретной задачи поиска массы, то можно составить интегральную сумму для некоторой непрерывной функции f(P), заданной на замкнутой, ограниченной фигуре G (можно говорить о замкнутой, ограниченной области, множестве). Это выражение вида

Рассмотрим предел этих интегральных сумм при Если этот предел не зависит ни от способа разбиения фигуры на части , ни от выбора точек P_i в каждой из частей, то его называют интегралом по мере(по фигуре) от функции f(P) и обозначают

. (2.1)

Конкретизируем введенные понятия для различных фигур.

I. Для отрезка [a, b] оси 0х (отрезок прямолинейного стержня, рис. 2.1)

(2.2)

− это обычный определенный интеграл.

Если − линейная плотность материала стержня, то (2.2) выражает его массу.

II. Для пространственной кривой l (рис. 2.2), т. е. G – это часть кривой, интеграл (2.1) принимает вид

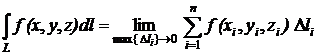. (2.3)

Если – функция линейной плотности массы, то (2.3) определяет массу криволинейного стержня.

Для плоской кривой выражение (2.3) немного упрощается:

. (2.4)

Интегралы (2.3) и (2.4) называются криволинейными интегралами по длине дуги, или криволинейными интегралами I рода.

III. В пространстве R² в качестве фигуры имеем ограниченную часть плоскости – область D (рис. 2.3). Тогда

, .

Интеграл (2.1) принимает вид

, (2.5)

где d_i – диаметр .

Интеграл (2.5) называется двойныминтегралом по области D.

Если – функция плотности массы, то (2.5) выражает массу неоднородной пластины.

IV. Для поверхности Q, где

, ,

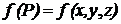интеграл (2.1) принимает вид

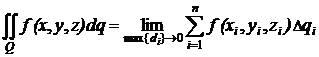(2.6)

и называется поверхностным интегралом по площади поверхности.

Если – функция поверхностной плотности массы, то (2.6) выражает массу поверхности Q.

V. Для пространственного тела Т (рис. 2.4), где

, ,

интеграл (2.1) принимает вид

(2.7)

и называется тройным интегралом по области Т.

Если − функция объемной плотности массы, то (2.7) выражает массу тела Т.

2.2. Основные свойства интеграла по мере области

1. Аддитивность относительно подынтегральной функции

(при этом каждый интеграл должен существовать).

Для доказательства достаточно учесть, что

2. Однородность

, С = const.

Это свойство следует из очевидного равенства

Объединяя свойства 1 и 2, можно сказать, что интеграл по мере области является линейным функционалом.

3. Если f (P) 1, то

Доказательство следует из определения интеграла по мере (формула (2.1)).

Конкретизируем это важное свойство:

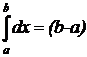· – длина отрезка ;

· – длина линии L;

· – площадь области D;

· – площадь поверхности Q;

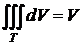· – объём тела Т.

4. Если , то

Например:

1) двойной интеграл по области G, которая является дугой кривой;

2) определенный интеграл, когда областью является точка, т. е. отрезок .

5. Аддитивность относительно области интегрирования

, если .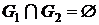

Доказательство

Рассмотрим область в пространстве R². Тогда

6. Теорема о знаке интеграла по мере.

Если .

Доказательство следует из определения интеграла по мере (формула (2.1)).

7. Если , то

Доказательство

Так как , то . Проинтегрируем обе части этого неравенства по области G:

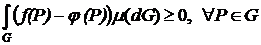Тогда

Из этого свойства следует, что неравенства можно почленно интегрировать.

8. Если , то

Доказательство следует из свойств 3 и 7.

Это свойство определяет двустороннюю оценку интеграла по мере.

9. Оценка модуля интеграла по мере области

Доказательство

По определению интеграла по мере имеем

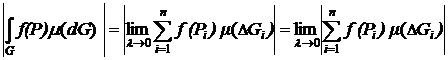Воспользуемся свойством модуля , тогда

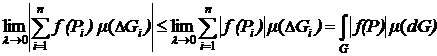Таким образом, получаем

10. Теорема о среднем значении функции в области с ненулевой мерой. Если функция f(P) непрерывна на замкнутой ограниченной фигуре G, то найдется такая точка , что

Доказательство

Так как фигура G ограничена и функция f(P) непрерывна, то функция f(P) принимает на G свои наибольшее и наименьшее значения, т. е.

Проинтегрируем это неравенство

Воспользуемся свойством 8

Разделим неравенство на :

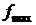т. е. величина заключена между и . Функция f(P) непрерывна и принимает значения между и 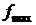. Значит, она должна принять и это значение в некоторой точке P₀. Таким образом,

2.3. Вычисление определенного интеграла

2.3.1. Формула Ньютона − Лейбница

Пусть 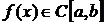. Как было показано ранее, определенным интегралом от функции f(x) по отрезку называется

, (2.8)

причем а называется нижним пределом интегрирования, b – верхним пределом интегрирования.

Если то величину определенного интеграла естественно принять за площадь криволинейной трапеции (рис. 2.7).

Формула, найденная Ньютоном и Лейбницем (независимо друг от друга), устанавливает связь между определённым и неопределённым интегралами. Она позволяет эффективно вычислять определенные интегралы и является основной формулой интегрального исчисления.

Разобьем отрезок на n частей (не обязательно равных по длине). Абсциссы границ полученных частей обозначим через :

Очевидно, справедливо равенство

(2.9)

Пусть Тогда по теореме Лагранжа

и формуле (2.9) можно придать вид

(2.10)

Формула (2.10) показывает, что при соответствующем выборе точек величина интегральной суммы при любом n постоянна и равна Поэтому при получим формулу

которую называют формулой Ньютона − Лейбница.

Определённый интеграл равен приращению первообразной от подынтегральной функции на отрезке интегрирования.

Для обозначения приращения функции на отрезке часто используют знак двойной подстановки

Формулу Ньютона − Лейбница можно вывести и другим способом.

Рассмотрим определённый интеграл

Для его существования необходимо, чтобы функция . Очевидно, что интеграл зависит от пределов интегрирования а и b.

Если закрепить а, а верхнюю границу сделать переменной, то интеграл

будет представлять некоторую функцию от х. Вычислим производную этой функции по переменной х. Для этого найдем

Тогда

Применим теорему о среднем

Перейдем к пределу при

так как при .

Итак, мы доказали теорему Барроу.

Теорема. Производная интеграла от непрерывной функции по переменному верхнему пределу равна подынтегральной функции, вычисленной на верхнем пределе.

Эта теорема является одной из основных теорем математического анализа и вскрывает глубокую связь между операциями определенного интегрирования и дифференцирования.

Следствие. Любая функция f(x), непрерывная на , имеет первообразную, выражаемую формулой

Исходя из геометрического смысла определённого интеграла как площади криволинейной трапеции, заметим, что соотношение

выражает переменную площадь криволинейной трапеции с основанием .

Теорема Барроу позволяет установить простой метод вычисления определённого интеграла.

Мы установили, что является первообразной для f(x). Первообразная имеет вид

Пусть х = а, тогда

Тогда . Подставим значение С в определение первообразной

Пусть теперь х = b, тогда

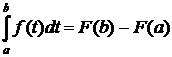Получили формулу Ньютона – Лейбница, которая устанавливает связь между определённым и неопределённым интегралами от непрерывной функции f(x).

2.3.2. Вычисление определённых интегралов
с помощью подстановки

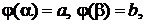
Теорема.Если С , причём функция отображает отрезок на отрезок , то

Доказательство

Пусть F(x) – первообразная для f(x), тогда

С другой стороны,

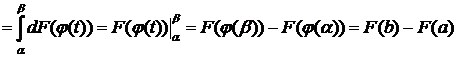При вычислении определённого интеграла с помощью подстановки возвращаться к прежней переменной интегрирования не нужно. Однако не следует забывать о необходимости изменения пределов интегрирования.

2.3.3. Вычисление определённых интегралов
путём интегрирования по частям

Формула интегрирования по частям для определённого интеграла выводится очень просто.

Пусть . Тогда

т. е.

2.4. Приближенное вычисление определённых
интегралов. Понятие о численном интегрировании

Пусть требуется вычислить определённый интеграл

от непрерывной функции f(x). Если может быть найдена первообразная F(x) подынтегральной функции f(x), то интеграл может быть вычислен по формуле Ньютона – Лейбница

Если же первообразная не может быть найдена или если f(x) задана графически или таблично, то для вычисления интеграла прибегают к приближенным формулам, точность которых может быть сделана сколь угодно большой.

Приближенные методы вычисления определенного интеграла в большинстве случаев основаны на том, что определенный интеграл численно равен площади криволинейной трапеции, ограниченной кривой y = f(x), отрезком оси 0х и вертикальными прямыми x = a, x = b. Благодаря этому задача о приближенном вычислении интеграла равносильна задаче о приближенном вычислении площади криволинейной трапеции. При этом кривая y = f(x) заменяется новой кривой, которая достаточно «близка» к данной. Тогда искомая площадь приближенно равна площади криволинейной трапеции, ограниченной новой кривой.

В качестве этой кривой выбирают такую, для которой площадь криволинейной трапеции подсчитывается просто. В зависимости от выбора новой кривой (метода аппроксимации) мы получаем ту или иную приближенную формулу, часто называемую квадратурной.

2.4.1. Формула прямоугольников

Формула прямоугольников основана на замене подынтегральной функции f(x) на кусочно-постоянную функцию.

Отрезок разбивается на n частей равной длины . На каждой из частей функция f(x) заменяется постоянной величиной 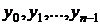. Тогда площадь криволинейной трапеции приближенно приравнивается к площади ступенчатой фигуры, составленной из прямоугольников (рис. 2.8).

Рис. 2.8

Тогда

– для случая вписанной ступенчатой фигуры (штриховка)

;

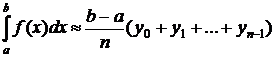– для случая описанной ступенчатой фигуры (пунктир)

Для повышения точности (уменьшения ошибки вычисления) требуется увеличивать n – число элементов разбиения отрезка на части. При этом резко возрастает количество вычислений.

2.4.2. Формула трапеций

Формула трапеций аналогична формулам прямоугольников, но f(x) заменяется на каждом отрезке длиной линейной функцией, а площадь – суммой площадей трапеций (рис. 2.9).

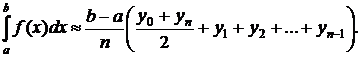
Рис. 2.9

Формулу трапеций можно получить как среднее арифметическое формул прямоугольников.

Формула трапеций точнее, чем формулы прямоугольников; объём вычислений остаётся почти таким же.

2.4.3. Формула парабол (Симпсона)

Формула парабол, предложенная английским математиком Симпсоном, основана на замене функции f(x) на отрезках длиной дугой параболы (рис. 2.10).

Рис. 2.10

Разобьем отрезок на четное число 2n равных отрезков

Через каждые 3 точки проводится дуга параболы . Таким образом, на участке кривая f(x) заменяется параболой. Мы осуществили кусочно квадратичную аппроксимацию. Площадь, ограниченную одной из парабол, нетрудно подсчитать:

Суммируя эти площади, в результате найдем приближенное значение интеграла

Заданная точность вычисления достигается за значительно меньшее число операций.

3. Несобственные интегралы

Понятие интеграла было введено для функций, непрерывных на конечном отрезке. Однако при рассмотрении математических моделей многих явлений (процессов) целесообразно обобщение понятия интеграла. Во-первых, иногда полезно рассмотрение бесконечных пределов интегрирования. Во-вторых, интегрируемая функция может иметь разрывы. В связи с изложенным мы рассмотрим эти ситуации и дадим соответствующие обобщения понятию интеграла.

3.1. Несобственные интегралы
с бесконечными пределами интегрирования

Пусть т. е. функция f(x) непрерывна на отрезке при любом b > a.

Интеграл

(3.1)

называется несобственным интегралом.

Говорят, что несобственный интеграл сходится, если существует конечный предел (3.1). Если не существует конечного предела (3.1), то несобственный интеграл называют расходящимся.

С геометрической точки зрения величина (3.1) выражает площадь бесконечной фигуры, ограниченной кривой осью абсцисс и прямой x = a
(рис. 3.1).

Аналогично вводятся и другие несобственные интегралы с бесконечными пределами интегрирования

где выбирается произвольно (докажите самостоятельно, что от выбора c значение интеграла не зависит). Для последнего интеграла сходимость определяется сходимостью обоих интегралов в правой части равенства.

Рассмотренные несобственные интегралы называют иногда несобственными интегралами первого рода.

3.2. Несобственные интегралы от разрывных функций

Пусть , а в точке x = b она имеет разрыв второго рода. Тогда интеграл

(3.2)

называется несобственным интегралом (сходящимся, если предел (3.2) существует и конечен; расходящимся – в остальных случаях). Несобственные интегралы от разрывных функций называют ещё несобственными интегралами второго рода.

Геометрический смысл несобственного интеграла ясен из рис. 3.3.

Аналогично вводятся несобственные интегралы в случаях, когда подынтегральная функция имеет иначе расположенную точку разрыва. Так, если f(x) имеет разрыв при x = a, т. е. , то

(3.3)

Если точка разрыва x = с лежит между точками x = a и x = b, то

(3.4)

3.3. Теоремы о сходимости несобственных интегралов

Вопрос о сходимости несобственного интеграла в ряде случаев можно решить без его вычисления. Это особенно важно, когда первообразную через элементарные функции в конечном виде выразить невозможно. Рассмотрим простейшие теоремы относительно сходимости несобственных интегралов с бесконечными пределами.

Теорема 1.Если и интеграл сходится, то сходится и интеграл Если при тех же предположениях интеграл расходится, то расходится и интеграл .

Доказательство

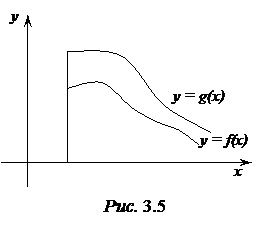Если существует, то представляет величину ограниченную и монотонно возрастающую. Так как , значит, и площадь, ограниченная этой кривой, меньше, чем площадь под кривой g(x) (рис. 3.5). Значит, существует и .

Вторая часть теоремы доказывается аналогично.

Теорема 2.Если сходится интеграл то сходится и интеграл .

Не приводя доказательства этой теоремы, заметим, что в первом интеграле суммируются площади, лежащие над и под осью абсцисс, а во втором интеграле площади под осью абсцисс учитываются со знаком минус (рис. 3.6). Поэтому первый интеграл сходится «труднее»: он может расходиться в тех случаях, когда второй интеграл сходится.

Если интеграл сходится, то интеграл называется абсолютно сходящимся.

Если интеграл сходится, а расходится, то первый интеграл называется условно сходящимся.

Теорема 3.Если и существует конечный ненулевой предел то интегралы , либо оба сходятся, либо оба расходятся.

Доказательство этой теоремы не приводим.

Наиболее часто при выяснении вопроса о сходимости несобственного интеграла выполняют сравнение его с интегралом от степенной функции

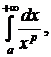(3.6)

который сходится при p > 1 и расходится при p

Действительно,

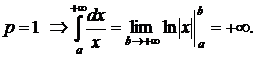
4. Интеграл как функция пределов
интегрирования. Понятие о специальных функциях, определяемых интегралами
с переменным верхним пределом

Определенный интеграл

можно рассматривать как функцию от а и b. Пусть a = const , а b обозначим через х. Тогда получим следующую функцию от х:

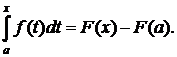(4.1)

Дифференцируя (4.1) по х с учётом того, что 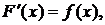получаем следующее правило дифференцирования определенного интеграла по переменному верхнему пределу:

(4.2)

Если верхний предел является функцией b(x), то

и вместо (4.2) будем иметь

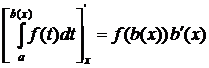Производная от элементарной функции всегда является элементарной функцией. Первообразная же от элементарной функции не всегда оказывается элементарной функцией. В связи с тем, что многие задачи математики и механики связаны с изучением и таких первообразных, возникает необходимость рассмотрения так называемых специальных функций, задаваемых при помощи интегралов с переменным пределом.

Так, в теории вероятности важную роль играет функция

(4.3)

которая называется нормальной функцией распределения.

Так как

то функция (4.3) монотонно возрастает. В дальнейшем мы увидим, что Для значений функции Ф(х) составлены таблицы.

Функция интегральный синус определяется интегралом

Особенность подынтегральной функции при t = 0 является устранимой.

Аналогично определяется интегральный логарифм

Используются и другие функции, определяемые при помощи интеграла с переменным верхним пределом.

5. Понятие об интегралах,
зависящих от параметра

Рассмотрим интеграл

(5.1)

Здесь величина х при интегрировании постоянна, но её значение можно выбирать по-разному, т. е. х является параметром. Очевидно, что в случае непрерывной по t функции 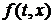формула (5.1) определяет некоторую функцию при Таким образом, функцию 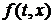считаем определенной в прямоугольнике

Количество параметров может быть и большим. Например,

Интегралы, зависящие от параметров, обладают следующими свойствами:

1) если функция 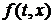то интеграл (5.1) определяет функцию и возможно интегрирование по параметру под знаком интеграла, т. е.

;

2) если частная производная то возможно дифференцирование по параметру под знаком интеграла (правило Лейбница), т. е.

Несобственные интегралы, зависящие от параметра, ведут себя несколько сложнее.

6. Понятие о гамма-функции

Рассмотрим интеграл, определяющий гамма-функцию (Г-функция, или эйлеров интеграл второго рода)

Этот интеграл зависит от параметра и является несобственным (с бесконечным верхним пределом). Кроме того, если х < 1, он имеет особенность при t = 0.

Установим основное свойство гамма-функции:

т. е.

(6.1)

Вычислим

Тогда, положив в (6.1) получим

т. е. гамма-функция является интерполирующей для факториала

(6.2)

С помощью формулы (6.2) можно определить 0!:

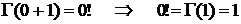Далее, используя формулу (6.1) как определяющую, имеем

при любых х. Поэтому можно продолжить для затем для и т. д. В результате получается функция, определенная всюду в R, кроме точек х = 0, –1, –2, … . Чтобы окончательно выяснить поведение Г-функции, найдем, как она изменяется при подходе к нулю справа и слева:

Очевидно, что в целочисленных отрицательных точках Г−функция будет вести себя как в нуле (рис. 6.1).

Рис. 6.1

7. Вычисление кратных интегралов

7.1. Вычисление двойного интеграла
в декартовых координатах

Рассмотрим ограниченную область .

Будем называть D правильной в направлении оси Oy, если она ограничена линиями и каждая прямая, параллельная оси Oy, проходящая через внутреннюю точку области, пересекает границу области D ровно в двух точках (рис. 7.1).

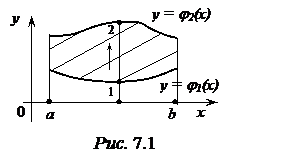Нижнюю из них (1) будем называть точкой входа, верхнюю (2) – точкой выхода.

Аналогично определяется область, правильная в направлении оси Ox (рис. 7.2).

Область, правильная в направлении обеих осей, называется правильной (нормальной).

Области более сложной формы обычно без особых затруднений можно разбить на несколько правильных областей. В качестве упражнения проделайте это с областью, изображенной на рис. 7.3 (область имеет «дыру»).

При вычислении двойного интеграла

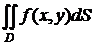(7.1)

будем считать, что область D правильная, а

Разобьем область D на элементарные прямоугольные участки прямыми, параллельными осям координат (рис. 7.4). Очевидно, что – площадь участка . На основании этого элемент площади в декартовых координатах записывают в виде Внутри каждого прямоугольника выберем точку .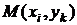

Выведем формулу для вычисления двойного интеграла (7.1)

Итак,

(7.2)

Интеграл, стоящий в правой части равенства (7.2), называется двукратным (или повторным) интегралом.

Из полученной формулы следует правило вычисления двойного интеграла: для вычисления интеграла (7.1) нужно проинтегрировать функцию f(x, y) по y (считая х постоянным) от до , затем проинтегрировать полученный результат по х в пределах от а до b (см. схему на рис. 7.5).

Дата добавления: 2018-02-18; просмотров: 717; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!