Интегрирование простейших дробей
Неопределенный интеграл
Первообразная и неопределенный интеграл
Пусть дана функция  Тогда производная
Тогда производная  Оператор, сопоставляющий функции её производную, называется оператором дифференцирования D:
Оператор, сопоставляющий функции её производную, называется оператором дифференцирования D:

Рассмотрим обратную задачу: зная функцию  найти функцию
найти функцию  , производная которой равна
, производная которой равна 
 (1.1)
(1.1)
Говорят, что функция F(x)является первообразной для функции f(x).
Теорема 1 (о виде первообразных). Любые две первообразные для одной и той же функции различаются лишь на постоянную величину.
Доказательство.Пусть F(x) и Ф(х) – две первообразные для функции f(x), т. е.

Таким образом, любая первообразная для заданной функции имеет вид

Здесь  – какая-либо первообразная; С – произвольная постоянная.
– какая-либо первообразная; С – произвольная постоянная.
Совокупность всех первообразных для функции f(x)называется неопределённым интегралом от функции f(x) и обозначается
 (1.2)
(1.2)
 В (1.2) f(x)называется подынтегральной функцией, f(x)dx – подынтегральным выражением. Процедура вычисления неопределённого интеграла называется интегрированием функции f(x).
В (1.2) f(x)называется подынтегральной функцией, f(x)dx – подынтегральным выражением. Процедура вычисления неопределённого интеграла называется интегрированием функции f(x).
Геометрический смысл неопределённого интеграла ясен из рис. 1.1, где показано множество кривых, каждая из которых может быть получена сдвигом кривой y = F(x)в направлении оси ординат. Неопределённый интеграл есть произвольный элемент y = F(x) + С указанного семейства кривых.
На неопределённый интеграл можно смотреть как на оператор, действующий из С в С1:
|
|
|

Оператор интегрирования иногда обозначают следующим образом:

имея в виду, что если заменить точку функцией f(x), то получится значение оператора на функции f(x).
Теорема 2 (о существовании неопределённого интеграла).Для всякой функции класса  существует неопределённый интеграл на том же отрезке
существует неопределённый интеграл на том же отрезке  .
.
В данном курсе доказательство этой теоремы не рассматривается.
1.2. Основные свойства неопределённого интеграла
1. Производная от неопределённого интеграла равна подынтегральной функции:
 (1.3)
(1.3)
Доказательство:

2. Дифференциал от неопределённого интеграла равен подынтегральному выражению

Доказательство:

3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

Доказательство:

4. Постоянный множитель можно выносить за знак неопределённого интеграла:
 (1.4)
(1.4)
Доказательство. Знак равенства в (1.4) понимается как совпадение производных для левой и правой частей. Отсюда следует очень простое доказательство


5. Неопределённый интеграл от суммы функций равен сумме интегралов от этих функций, если интегралы существуют:
|
|
|
 (1.5)
(1.5)
Доказательство. Доказательство проводится аналогично доказательству свойства 4:
 ,
,

Из равенств (1.4), (1.5) следует, что оператор интегрирования является линейным оператором.
1.3. Таблица основных интегралов
Приведём основные формулы для интегрирования элементарных функций. Часть этих формул известна из школьного курса математики.
1. 
2. 

частный случай 

3. 
4. 

5. 
6. 
7. 
8. 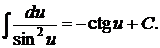
9. 
10. 
11. 
12. 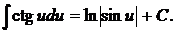
13. 
14. 
15. 
16. 
Приведенные формулы проверяют с помощью дифференцирования. Например, проверим формулу 15:

Аналогично убеждаемся в справедливости формулы 3:
 .
.
В качестве упражнения докажите справедливость формул 13, 14, 16.
1.4. Замена переменной в неопределенном интеграле. Интегрирование подстановкой
Выполним в интеграле  формальную замену переменной интегрирования
формальную замену переменной интегрирования 
 (1.6)
(1.6)
Проверим полученную формулу, вычислив производные по x от левой и правой частей равенства:



Таким образом, формула (1.6) доказана. При этом считалось, что

Формула (1.6) выражает метод интегрирования подстановкой, или метод замены переменной интегрирования. Этот метод целесообразно использовать в тех случаях, когда интеграл в правой части равенства (1.6) проще, чем в левой. После вычисления нового интеграла приходится возвращаться к старой переменной, для чего находят обратную функцию 
|
|
|
1.5. Интегрирование по частям
Второй из основных методов интегрирования базируется на формуле, выражающей дифференциал произведения:

Отсюда имеем

или, рассматривая левую и правую части равенства как подынтегральные выражения, получаем
 (1.7)
(1.7)
Произвольная постоянная в правой части равенства не пишется.
Формула (1.7) выражает метод интегрирования по частям. Этот метод уместно использовать в тех случаях, когда функция u(x)при дифференцировании упрощается. Поэтому в качестве u(x)выбирают функции  (по возрастанию сложности).
(по возрастанию сложности).
1.6. Интегрирование функций,
содержащих квадратный трехчлен
1. Интегралы вида  .
.
Выделим полный квадрат в знаменателе дроби:
 .
.
В зависимости от знака выражения  интеграл сведется
интеграл сведется


2. Интегралы вида  .
.
Выделим в числителе производную от знаменателя. Для этого числитель представим в виде
 .
.
Тогда
 .
.
В первом интеграле числитель является производной от знаменателя. Поэтому
 .
.
Второй интеграл рассмотрен в п. 1.
3. Интегралы вида  .
.
Выделим полный квадрат в подкоренном выражении
|
|
|


Интеграл сведется к табличным интегралам 15 или 16.
4. Интегралы вида  .
.
Для нахождения этого интеграла выделим в числителе производную квадратного трехчлена, стоящего под знаком корня, и разложим интеграл на сумму двух интегралов


Первый из интегралов есть табличный интеграл
 ,
,
а второй рассмотрен в п. 3.
1.7. Интегрирование рациональных дробей
Интегрирование простейших дробей
Рациональной дробью называется дробь вида  , где P(x) и Q(x) – многочлены. Рациональная дробь называется правильной, если степень многочлена P(x) ниже степени многочлена Q(x); в противном случае дробь называется неправильной.
, где P(x) и Q(x) – многочлены. Рациональная дробь называется правильной, если степень многочлена P(x) ниже степени многочлена Q(x); в противном случае дробь называется неправильной.
Простейшими (элементарными) дробями называются правильные дроби следующего вида:
А.  .
.
Б.  , где m – целое число, большее единицы.
, где m – целое число, большее единицы.
В.  .
.
Г.  , где n – целое число, большее единицы.
, где n – целое число, большее единицы.
Рассмотрим интегралы от простейших дробей:
А.  .
.
Б.  .
.
Вычисление интегралов от функций типа В было рассмотрено ранее в п. 1.6 «Интегрирование функций, содержащих квадратный трехчлен».
Г. Рассмотрим теперь частный случай интеграла от простейшей дроби типа Г. Для интеграла  (n – целое положительное число) имеет место следующая рекуррентная формула:
(n – целое положительное число) имеет место следующая рекуррентная формула:
 .
.
Эта формула позволяет после (n-1)-кратного применения свести данный интеграл In к табличному интегралу  .
.
1.7.2. Интегрирование рациональных дробей с помощью
разложения на простейшие дроби
Интегрирование рациональной дроби  проводится по следующему алгоритму:
проводится по следующему алгоритму:
1) если дана неправильная рациональная дробь, то необходимо выделить из нее целую часть, т. е. представить в виде
 ,
,
где M(x) – многочлен, а  – правильная рациональная дробь;
– правильная рациональная дробь;
2) разложить знаменатель дроби на линейные и квадратичные множители:
 ,
,
где  , т. е. трехчлен
, т. е. трехчлен  имеет комплексные сопряженные корни;
имеет комплексные сопряженные корни;
3) правильную рациональную дробь разложить на простейшие дроби:

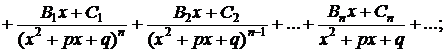
4) вычислить неопределенные коэффициенты  . Для этого привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной х произвольные числовые значения.
. Для этого привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной х произвольные числовые значения.
В результате интегрирование рациональной дроби сведется к нахождению интегралов от многочлена и от простейших рациональных дробей.
Случай 1. Знаменатель имеет только действительные различные корни.
Случай 2. Знаменатель имеет только действительные корни, причем некоторые из них – кратные.
Случай 3. Среди корней имеются простые комплексные корни.
Случай 4. Среди корней знаменателей имеются кратные комплексные корни, т. е. разложение знаменателя содержит повторяющиеся квадратичные множители.
1.8. Интегрирование иррациональных функций
1. Интегралы вида  ,где R – рациональная функция; m1, n1, m2, n2, … – целые числа
,где R – рациональная функция; m1, n1, m2, n2, … – целые числа
С помощью подстановки  , где s – наименьшее общее кратное чисел n1, n2, …, указанный интеграл преобразуется в интеграл от рациональной дроби.
, где s – наименьшее общее кратное чисел n1, n2, …, указанный интеграл преобразуется в интеграл от рациональной дроби.
2. Интегралы вида 
Такой интеграл приводится к интегралу от рациональной функции новой переменной с помощью следующих подстановок Эйлера.
Первая подстановка Эйлера. Если  , то полагаем
, то полагаем
 .
.
Перед корнем  возьмем для определенности знак плюс. Тогда
возьмем для определенности знак плюс. Тогда
 ,
,
откуда x определяется как рациональная функция от t:

(значит, dx тоже будет выражаться рационально через t), следовательно,
 ,
,
т. е.  оказывается рациональной функцией от t.
оказывается рациональной функцией от t.
Так как  , x и dx выражаются рационально через t, то, следовательно, данный интеграл преобразуется в интеграл от рациональной функции от t.
, x и dx выражаются рационально через t, то, следовательно, данный интеграл преобразуется в интеграл от рациональной функции от t.
3. Интегралы вида 
С помощью подстановки  этот интеграл приводится к рассмотренному в п. 1.8.2.
этот интеграл приводится к рассмотренному в п. 1.8.2.
4. Интегралы дифференциальных биномов  ,где m, n, p – рациональные числа
,где m, n, p – рациональные числа
Интегралы от дифференциальных биномов выражаются через элементарные функции только в трех случаях:
1) p – целое число; тогда данный интеграл сводится к интегралу от рациональной функции с помощью подстановки  , где s – наименьшее общее кратное знаменателей дробей m и n;
, где s – наименьшее общее кратное знаменателей дробей m и n;
2)  –целое число; в этом случае данный интеграл рационализируется с помощью подстановки
–целое число; в этом случае данный интеграл рационализируется с помощью подстановки  , где s – знаменатель дроби p;
, где s – знаменатель дроби p;
3)  – целое число; в этом случае к той же цели ведет подстановка
– целое число; в этом случае к той же цели ведет подстановка  , где s – знаменатель дроби p.
, где s – знаменатель дроби p.
1.9. Интегрирование тригонометрических функций
1. Интегралы вида  , где R – рациональная функция
, где R – рациональная функция
Интегралы указанного вида приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки  .
.
В результате этой подстановки имеем
 ;
;  ;
;
 .
.
2. Интегралы вида 
Выделим два случая решения такого интеграла:
1) если n – нечетное положительное число, то применяется подстановка  ; если же m – нечетное положительное число, то подстановка
; если же m – нечетное положительное число, то подстановка  ;
;
2) если оба показателя степени m и n – четные положительные числа, то следует преобразовать подынтегральную функцию с помощью формул
 ,
,
 ,
,
 .
.
3. Интегралы вида  и
и  ,где m – целое положительное число
,где m – целое положительное число
При нахождении таких интегралов применяются формулы
 или
или  ,
,
с помощью которых последовательно понижается степень тангенса или котангенса.
4. Интегралы вида  ,
, ,
,
Тригонометрические формулы
 ,
,
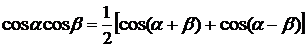 ,
,

дают возможность представить произведение тригонометрических функций в виде суммы.
Дата добавления: 2018-02-18; просмотров: 797; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
