Методы решения задач линейного программирования
Изучим симплексный метод решения задач линейного программирования. Рассмотрим использование надстройки Excel для поиска оптимальных решений задач методами математического программирования.
Симплексный метод
Для практического решения задач геометрические соображения (с вычерчиванием многоугольника) годятся в основном в двумерном случае (иногда в трехмерном). Для случая n переменных разработан алгоритм, который носит название симплекс-метода.
Математический аппарат симплексного метода решения задач линейного программирования разработал американский математик Дж. Данциг (1951 г.)[2]. Симплексный метод находит применение для широкого круга задач линейного программирования и до настоящего времени является одним из основных методов.
Симплексный метод – это метод целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчета найти оптимальное решение, либо установить, что оптимального решения не существует.
Симплексный метод применяется для задачи линейного программирования, заданной в канонической форме, которую можно сформулировать следующим образом.
Требуется найти максимальное значение целевой функции (функционала) 
,
где 
, при ограничениях
Предполагается, что 
Алгоритм симплекс-метода
Шаг 0. В матрице А есть фрагмент, содержащий единичную матрицу. Переменные 
принимаем за базисные переменные. Базисные переменные входят в целевую функцию с нулевыми коэффициентами. Остальные переменные 
считаются свободными или небазисными.
|
|
|
Процесс оптимизации начнем с выбора некоторого опорного решения. Положим все небазисные переменные равными нулю: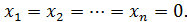 
В результате получаем первоначальный опорный план
,
который соответствует одной из угловых точек (вершин) области допустимых решений.
Шаг 1. Для исследования плана на оптимальность построим симплекс-таблицу:
| с1 | с2 | сn | 0 | 0 | 0 | |||||||
| Коэффициенты целевой функции, СБ | Базис хБ | Свободные члены b | 
| 
| 
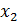
| y1 | y2 | ym | ||||
| d Строка оценок |
Считаем оценки:
где
– столбец коэффициентов при базисных векторах в целевой функции;
– j-й столбец в матрице А;
– столбец коэффициентов при j-й переменной в целевой функции;
|
|
|
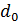– значение целевой функции для текущих базисных переменных;
при этом значения базисных переменных берутся из столбца b, анебазисных – равны нулю.
Оценки 
характеризуют прирост целевой функции при включении в базис небазисной переменной 
Оценки у базисных переменных всегда равны нулю.
Шаг 2. Просматриваем строку оценок.
Если все 
( 
), то задача решена, так как для оптимальности опорного решения в задаче на максимум требуется выполнение неотрицательности всех оценок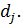 
В этом случае в столбце b находятся оптимальные значения базисных переменных.
Если есть 
, то решение можно улучшить.
Шаг 3. Ищем j: . (Обычно берется наибольшая по модулю отрицательная оценка .) j-й столбец – разрешающий.
Шаг 4. Просматриваем разрешающий столбец.
Если все 
, то 
неограничен (т.е. равен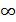 
).
В противном случае ищем к-ю разрешающую строку:
Разрешающая строка соответствует меньшему из отношений свободных членов к положительным элементам разрешающего столбца.
Шаг 5. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки – разрешающий: 
.
Шаг 6. Строим новую симплекс-таблицу.
I способ. Делим разрешающую строку на разрешающий элемент. Остальные элементы таблицы рассчитываются по правилу прямоугольника:
|
|
|
или
II способ. Делаем разрешающий элемент равным 1: 
, а все остальные элементы этого разрешающего столбца (j-го) – равными 0 (методом Гаусса).
| l | j |
| ||||
| i | 
| 
| ||||
| k | 
|
|
| |||
i 
|
При этом j-я переменная заходит в базис, а k-я – из базиса выходит.
Описанную процедуру повторяем заново.
Теорема. Если после очередной итерации имеется отрицательная оценка, а в столбце с отрицательной оценкой имеется хотя бы один положительный элемент, то решение задачи можно улучшить, проведя очередную итерацию.
Если в столбце с отрицательной оценкой нет ни одного положительного элемента, то задача решения не имеет, так как целевая функция стремится к бесконечности.
Дата добавления: 2018-02-18; просмотров: 909; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!