Функция распределения случайной величины.
Случайные величины
В теории вероятности помимо традиционных задач, состоящих в нахождении вероятностей соответствующих событий, возникает ряд специфических вопросов, таких, как определение вероятного количества бракованных изделий, среднего времени безотказной работы прибора и т.д.
В связи с этим в теории вероятности вводится понятие случайной величины.
Под случайной величиной понимают переменную величину, которая может принимать то или иное значение, в зависимости от хода испытаний. Обозначается X или Y.
Определение
Пусть Ω – множество исходов испытания,  - совокупность его подмножеств (событий),
- совокупность его подмножеств (событий),  - вероятность (неотрицательная функция на
- вероятность (неотрицательная функция на  , удовлетворяющая соответствующим свойствам).
, удовлетворяющая соответствующим свойствам).
Тогда случайной величиной X называется функция, отображающая множество Ω во множество действительных чисел R:
 ,
,
(т.е. каждому исходу испытания ω соответствует определенное число – значение случайной величины).
При этом
 ,
,
т.е. для любого действительного числа x неравенство  является событием и, значит, имеет некоторую вероятность. ◄
является событием и, значит, имеет некоторую вероятность. ◄
Если говорят, что задача случайна X, то предполагается, что имеется испытание, в котором наблюдается эта величина, и существуют вероятности событий вида:  ,
,  ,
,  , где x, a, b
, где x, a, b  R. Случайный характер случайных величин проявляется в том, что различные значения она может принимать с теми или иными вероятностями.
R. Случайный характер случайных величин проявляется в том, что различные значения она может принимать с теми или иными вероятностями.
Зависимость между возможными значениями случайных величин и соответствующими вероятностями называется законом распределения случайных величин.
|
|
|
Примеры
1. Испытание – бросание игральной кости. Случайная величина – количество выпавших очков. Множество значений случайной величины -  .
.
2. Эксперимент – бросание монеты 10 раз подряд. Случайная величина – количество появления герба. Множество значений случайной величины -  .
.
3. Эксперимент – контроль за работой прибора. Случайная величина – время безотказной работы прибора. Множество значений случайной величины – интервал  .
.
Дискретные случайные величины.
Закон распределения дискретных случайных величин.
Дискретной случайная величина называется такую случайную величину, множество возможных значений которой либо конечное, либо бесконечное, но счетное.
Пусть X - дискретная случайная величина, имеющая n различных значений 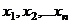 .
.
Равенства  ,
,  ,…
,…  являются событиями, образуют полную группу событий и, значит, имеют некоторую вероятность. Обозначим
являются событиями, образуют полную группу событий и, значит, имеют некоторую вероятность. Обозначим  вероятности этих событий, т.е.
вероятности этих событий, т.е.
 ,
,  .
.
Функциональная зависимость между возможными значениями случайной величины и соответствующими вероятностями – простейшая форма закона распределения дискретных случайных величин, а ее табличное представление называется рядом распределения дискретных случайных величин:
|
|
|

| 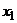
| 
| … | 
|

| 
| 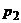
| … | 
|
Т.к. события образуют полную группу, то
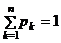 . (2.1)
. (2.1)
Если множество значений дискретных случайных величин бесконечно (счетно), то сумма в формуле (1.1) заменяется рядом  , при этом ряд не может быть представлен таблицей.
, при этом ряд не может быть представлен таблицей.
Пример
4. Случайная величина X – количество очков, выпавших при бросании игральной кости. Множество значений случайной величины -  , т.е.
, т.е.  и если кость правильная, то
и если кость правильная, то  .
.
Ряд распределения:

| 1 | 2 | 3 | 4 | 5 | 6 |

| 
| 
| 
| 
| 
| 
|
Функция распределения случайной величины.
Функцией распределения случайной величины Х называется функция, ставящая в соответствии каждому значению аргумента х вероятность того, что случайная величина Х примет значение, меньше, чем х:
 (2.2)
(2.2)
Геометрическое значение:  есть вероятность того, что значение случайной величины X расположится на числовой оси левее точки x.
есть вероятность того, что значение случайной величины X расположится на числовой оси левее точки x.
|
|
|
Зная функцию распределения случайной величины, можно найти вероятность попадания случайной величины в любой интервал:
 . (2.3)
. (2.3)
■ По определению функции распределения имеем:
 ,
,  .
.
Обозначим: событие  ,
,  ,
,  ,
,  , а т.к. события
, а т.к. события  и
и  несовместны, то
несовместны, то  , что и требовалось доказать. ■
, что и требовалось доказать. ■
Свойства функции распределения случайной величины:
1°  , т.к. F(x) – вероятность (
, т.к. F(x) – вероятность (  );
);
2°  - неубывающая функция;
- неубывающая функция;
Док-во: Возьмем два произвольных значения 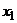 и
и  ,
,  . Тогда по формуле (2.3) имеем:
. Тогда по формуле (2.3) имеем:
 ,
,
а т.к. вероятность события всегда неотрицательна, то  , т.е.
, т.е.  - функция неотрицательная.
- функция неотрицательная.
3°  ; доказательство:
; доказательство:  - достоверное событие;
- достоверное событие;
4°  ; доказательство: т.к.
; доказательство: т.к.  , то
, то  - невозможное событие.
- невозможное событие.
Дата добавления: 2018-02-18; просмотров: 834; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
