Математическое описание непрерывных двумерных сигналов на примере изображений
Распределение энергии источника светового излучения по пространственным координатам 
времени 
и длинам волн 
можно описать функцией
. (2.158)
Энергия излучения пропорциональна квадрату амплитуды и поэтому представляет собой действительную положительную величину.
В целях упрощения моделей считают, что изображения отличны от нуля только в ограниченной области 
, 
и наблюдаются в течение конечного промежутка времени 
.
Таким образом, функция является ограниченной функцией четырех ограниченных переменных.
Ощущение светлоты, возникающее в зрительной системе человека, обычно определяется мгновенной яркостью светового поля, то есть величиной
, (2.159)
где 
- спектральная чувствительность человеческого зрения.
В технических устройствах вводят аналогичную функцию, которая описывает изображение для i-й спектральной зоны:
, (2.160)
где 
- спектральная чувствительность i-того датчика.
Функция 
представляет собой распределение яркости или какой-либо другой физической величины, связанной с яркостью. Очень часто, особенно при работе с изображениями, аргумент t меняется дискретно, поэтому в дальнейшем аргумент t можно опустить.
При моделировании систем обработки двумерных сигналов вводится понятие двумерной линейной системы. Система называется линейной, если к ней применим принцип суперпозиции, то есть
|
|
|
, (2.161)
где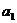 
, 
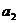- некоторые постоянные;
- оператор, описывающий преобразование входного сигнала;
, 
- двумерные функции.
Используя свойство дельта-функции, сигнал на входе системы 
можно представить как взвешенную сумму дельта-функций
, (2.162)
где 
- весовой множитель дельта-функции, имеющего координаты 
на плоскости .
Если на входе линейной системы действует сигнал , то на выходе имеет место сигнал
(2.163)
или
. (2.164)
Можно поменять местами операции линейного преобразования и интегрирования, так как линейный оператор действует только на тот множитель подинтегрального выражения, который зависит от пространственных переменных .
Запишем второй множитель подинтегрального выражения в виде
(2.165)
и будем называть эту функцию импульсным откликом двумерной системы. Подстановка 
в соотношение (2.164) дает интеграл суперпозиции
. (2.166)
Линейная двумерная система называется пространственно-инвариантной, если ее импульсный отклик зависит только от разности координат 
и 
. Для такой системы
|
|
|
(2.167)
и интеграл суперпозиции имеет особую форму, называемую интегралом свертки
. (2.168)
Операция свертки символически записывается так
. (2.169)
Свойства интеграла свертки.
1. Интеграл свертки симметричен, то есть
. (2.170)
2. Спектр функции, полученной в результате свертки двух функций и 
равен произведению спектров исходных функций, то есть
, (2.171)
где 
- спектр функции ;
- спектр функции .
3. Спектр функции, полученной в результате перемножения двух функций и , пропорционален свертке спектров исходных функций, то есть
, (2.172)
где - спектр функции;
- спектр функции.
Наряду с одномерными сигналами, которые рассмотрены ранее, при моделировании различных полей, например, изображениями, приходится иметь дело с двумерными сигналами. К таким сигналам также может быть применено преобразование Фурье, которое в этом случае носит название двумерного. В результате двумерного преобразования Фурье сигнал , описывающий, скажем, изображение, преобразуется в двумерный спектр (двумерную спектральную плотность) 
этого изображения, который определяется из соотношения
|
|
|
, (2.173)
где 
, 
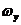- пространственные частоты вдоль оси x и y.
В общем случае спектр есть комплексная величина. Ее можно разложить на действительную и мнимую части:
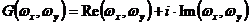, (2.174)
и представить с помощью амплитуды и фазы
, (2.175)
где 
;
. (2.176)
Достаточным условием существования Фурье-спектра функции является абсолютная интегрируемость этой функции:
. (2.177)
По известному Фурье-спектру может быть восстановлено исходное изображение 
:
. (2.178)
Это преобразование называется обратным двумерным преобразованием Фурье.
Свойства двумерного преобразования Фурье.
1. Если функция разделима по пространственным переменным, так что 
, то
, (2.179)
где 
и 
- одномерные Фурье-спектры функций 
и 
.
2. Оператор двумерного преобразования Фурье линеен
. (2.180)
3. Изменение масштаба пространственных переменных приводит к обратному изменению масштаба пространственных частот и пропорциональному изменению значений спектра
|
|
|
. (2.181)
4. Сдвиг (изменение координат) на исходной плоскости приводит к фазовым изменениям на частотной плоскости
. (2.182)
Наоборот, сдвиг на частотной плоскости вызывает фазовые изменения исходной функции
. (2.183)
При цифровой обработке изображений их обычно представляют в виде массива чисел, полученных в результате дискретизации исходного изображения по пространственным переменным. После обработки получают новые числовые массивы, используемые для восстановления изображений, используемых человеком. Отсчеты изображения получают в результате измерения некоторых физических характеристик реального изображения. При дискретизации и восстановлении непрерывных изображений обрабатываемые изображения обычно рассматривают как детерминированные поля.
Пусть функция 
описывает непрерывное изображение, представляющее собой распределение яркости, оптической плотности или какого-либо другого параметра изображения. В идеальной системе дискретизации изображений пространственные отсчеты исходного изображения получаются путем перемножения функции с пространственно-дискретизирующей функцией
, (2.184)
состоящей из бесконечного числа дельта-функций, заданных в узлах решетки с шагом 
(рис.2.17).
 |
Тогда дискретизированное изображение описывается выражением
, (2.185)
в котором учитывается, что функцию можно внести под знак суммирования и задать ее значения только в точках отсчета.
Для анализа процесса дискретизации удобно использовать спектр 
, получаемый в результате непрерывного двумерного преобразования Фурье дискретизированного изображения
. (2.186)
В силу свойства спектра свертки, спектр дискретизированного изображения можно представить в виде свертки спектра исходного изображения 
и спектра дискретизирующей функции 
, то есть
. (2.187)
Двумерное преобразование Фурье дискретизирующей функции дает бесконечный набор дельта-функций в плоскости пространственных частот с шагом 
и 
. Таким образом,
. (2.188)
Так как спектр реального изображения ограничен, то есть 
при 
и 
, то вычисляя с помощью (2.187) свертку, найдем
. (2.189)
Меняя порядок операции суммирования и интегрирования и учитывая основное свойство дельта-функции получаем выражение для спектра дискретизированного изображения
. (2.190)
На рис.2.18а изображен типичный спектр исходного изображения, а на рис.2.18б - спектр дискретизированного исходного изображения.
 |
Из рис.2.18 видно, что спектр дискретизированного изображения получается путем бесконечного повторения спектра исходного изображения со сдвигом на величину, кратную 
и 
вдоль оси и 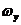соответственно. Если 
и 
выбраны слишком большими по сравнению с шириной спектра , то соседние спектры будут перекрываться друг с другом, что сделает невозможным восстановление исходного изображения.
Из отсчетов функции 
можно получить непрерывное изображение путем линейной пространственной интерполяции или с помощью линейной пространственной фильтрации дискретизированного изображения. Если 
- импульсный отклик интерполирующего фильтра, 
- его частотная характеристика, то восстановленное изображение получается как свертка последовательности отсчетов с импульсным откликом восстанавливающего фильтра:
, (2.191)
где 
- восстановленное изображение.
Подставив значение из равенства (2.190), получим:
. (2.192)
Импульсный отклик 
выполняет роль двумерной функции, интерполирующей отсчеты на всю плоскость. Пространственно частотный спектр изображения, восстановленного согласно выражению (2.191), (по свойству свертки) равен произведению частотной характеристики восстанавливающего фильтра на спектр дискретизированного изображения:
. (2.193)
Подставив выражение для спектра дискретизированного изображения получим:
. (2.194)
Очевидно, что если спектры не перекрываются, а множитель подавляет все сдвинутые спектры при 
, то спектр восстановленного непрерывного изображения будет совпадать со спектром исходного изображения и поэтому изображения также будут одинаковыми. Для изображений с ограниченной шириной спектра 
и 
первое условие выполняется, если интервал дискретизации выбран так, что прямоугольная область, ограниченная верхними граничными частотами спектра (рис.2.19) лежит внутри прямоугольной области, определяемой половинами частот дискретизации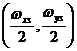 
.
 |
То есть выполняются неравенства
, 
(2.195)
или
, 
. (2.196)
Это значит, что шаг дискретизации не должен превышать половины периода пространственной гармоники, соответствующей самым мелким деталям изображения. Это условие эквивалентно теореме Котельникова о дискретизации одномерных сигналов. В этом случае, когда отсутствует наложение спектров, исходное изображение можно абсолютно точно восстановить путем пространственной фильтрации с помощью соответствующего фильтра.
В реальных системах дискретизации изображений дискретизирующая решетка имеет конечные размеры, ширина дискретизирующих импульсов заметно отличается от нуля, а отсчеты изображения могут быть взяты с недостаточной частотой. Кроме этого, искажения могут вноситься оптической системой и сканирующей диафрагмой.
Рассмотрим влияние некоторых из этих факторов.
1. Если спектр изображения ограничен по ширине, а и удовлетворяет теореме Котельникова, то конечная ширина импульса дискретизации приводит к тем же результатам, как если бы исходное изображение перед идеальной дискретизацией подверглось линейному искажению (смазыванию). Однако конечность размеров дискретизирующего импульса не всегда является недостатком. В случае, если спектр исходного изображения очень широкий и оно дискретизируется с недостаточной частотой, то импульс с конечными размерами фактически осуществляет низкочастотную фильтрацию исходного изображения, что приводит к сужению спектра и, следовательно, уменьшает ошибки, вызванные наложением спектров.
2. Если отсчеты изображения взяты с недостаточной частотой, то имеет место наложение спектров, что ведет к тому, что в восстановленном изображении будут внесены ложные пространственные гармоники. (В оптике это явление называют муар-эффектом).
Действительно из (2.190) видно, что спектр дискретизированного изображения можно представить в виде
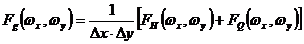, (2.197)
где - описывает спектр исходного изображения, дискретизированного с периодом , ,
а слагаемое
(2.198)
описывает те компоненты спектра дискретизированного изображения, которые получаются при повторении исходного спектра с периодами и . На рис.2.20 изображен спектр двумерной функции, дискретизированной с недостаточной частотой.
 |
При отсутствии наложения спектров оптимальную интерполяцию отсчетов изображения можно получить, пропуская дискретизированное изображение через идеальный фильтр нижних частот.
Дата добавления: 2018-02-18; просмотров: 747; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!