Алгоритм Берлекэмпа-Мэсси для исправления ошибок и стираний
• Итерация 0: Начальные установки.

• Итерация 1:

• Итерация 2:

• Итерация 3:

• Итерация 4
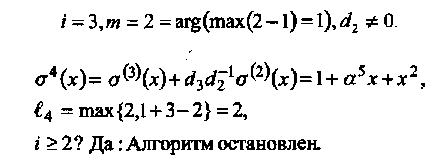
Таким образом, получаем многочлен локаторов ошибок

Напомним, что в последнем равенстве с помощью процедуры Ченя найдены обратные величины локаторов ошибок в поле GF(2m). Действительно, проверка дает σ(а12) = 0 и о(а3) = 0. Следовательно, локаторами ошибок являются а-12 = а3 иa-3 = а12.
Из определения (4.12) находим модифицированный многочлен значений искажений
 (4.18)
(4.18)
Многочлен локаторов искажений равен

и, следовательно, ф'(х) = 1.
Значения ошибок и стираний могут быть вычислены по формулам (4.14) и (4.15), соответственно,

Отсюда следует, что многочлен искажений равен

Результат декодирования v(x) = г(х) + е(х) совпадает с переданным словом v(x). Исправлены две ошибки и два стирания.
Прямое вычисление значений искажений
Для кодов PC с малым кодовым расстоянием значения стираний можно получить как решение системы линейных уравнений. Пусть е(х) полином ошибок, ассоциированный с комбинацией v ошибок и μ стираний,
 (4.19)
(4.19)
Тогда справедлива следующая система линейных уравнений, аналогичная (4.8), связывающая синдромы и значения искажений:
 (4.20)
(4.20)
где 1 ≤i≤ 2td. Как и раньше, может быть использовано любое подмножество v +μ≤td уравнений для определения значений всех стираний и ошибок.
|
|
|
Пример 44.Рассмотрим прямое вычисление значений искажений из предыдущего примера. После выполнения алгоритма Берлекэмпа-Мэсси и процедуры Ченя декодеру известны локаторы искажений и многочлен ошибок в виде

Значения искажений могут быть найдены из системы линейных уравнений (4.20), которая в матричной форме имеет
следующий вид
 (4.21)
(4.21)
Легко проверить, что решением (4.21) являются f0 = а14, е3 = а8,f5 = а5, e12 = а. Эти значения совпадают со значениями искажений, вычисленными модифицированным алгоритмом Форни.
4.4. Распределение весов
Как упоминалось выше, коды PC являются МДР кодами. Распределение весов МДР кодов вычисляется точно с помощью следующего выражения [MS, LC]:
Число кодовых слов веса i МДР (n,k,d) кода над GF(q) равно
 (4.22)
(4.22)
Для оценки помехоустойчивости (n,k,d) PC кода над GF(q) можно использовать следующую границу (оценку сверху) вероятности ошибки на бит Рb алгебраического декодера PC2, которая легко вычисляется и дает достаточно хороший результат,
 (4.23)
(4.23)
где Ps вероятность ошибки на символ на входе декодера PC,
|
|
|

и р вероятность ошибки на бит на входе декодера. Вероятность ошибки на слово (включая неправильное декодирование и отказ от декодирования) ограничена сверху границей (1.31),
 (4.24)
(4.24)
Вопросы для самоконтроля
1. Расскажите о работе алгоритма Мэсси по декодированию кода РС
2. Расскажите о работе алгоритма Евклида по декодированию кода РС
3. Опишите принципы работы алгоритма Берлекэмпа-Мэсси для исправления ошибок и стираний
4. Как рассчитывается распределение весов для РС кода
ГЛОССАРИЙ
Кодовое слово - последовательность информационных и избыточных символов образующих кодовую последовательность;
Хеммингово расстояние - число позиций, на которых два двоичных вектора не совпадают;
Корректирующей способностью кода – способность кода исправлять t ошибок в принятом слове;
Стандартной таблицей (или стандартной расстановкой) для двоичного линейного (n, k, dmin) кода С называется таблица всех возможных принятых из канала векторов r, организованная таким образом, что может быть найдено ближайшее к r кодовое слово v;
Совершенными кодами называются коды удовлетворяющие границе Хемминга с равенством;
|
|
|
Вероятность правильного декодирования равна вероятности того, что вектор ошибок совпадает с одним из лидеров смежных классов;
Код Хемминга – это совершенный код, исправляющий одну ошибку;
Код Голея – совершенный код с параметрами (23,12,7)
Линейный блоковый код является циклическим тогда и только тогда, когда любой циклический сдвиг любого кодового слова оказывается другим (или тем же самым) кодовым словом;
CRC коды избыточные циклические коды для обнаружения ошибок.
ЛИТЕРАТУРА
(добавленная при переводе)
Э. Берлекэмп, Алгебраическая теория кодирования, «Мир», Москва 1971.
Р. Блейхут, Теория и практика кодов, исправляющих ошибки, «Мир», Москва, 1986.
Э. Л. Блох и В. В. Зяблов, Обобщенные каскадные коды, «Связь», Москва, 1976.
Э. Л. Блох и В. В. Зяблов, Линейные каскадные коды, «Наука», Москва 1982. Кларк и Кейн,
Г. С. Евсеев, «О сложности декодирования линейных кодов», Проблемы передачи информации, т. 19, №1, стр. 3-8, 1983.
Д. Форни, Каскадные коды, «Мир», Москва, 1970.
Р. Галлагер, Коды с малой плотностью проверок на четность, «Мир», Москва, 1966.
Р. Галлагер, Теория информации и надежная связь. «Советское радио», Москва 1974.
Р. Лидл и Г. Нидерайтер. Конечные поля, т. 1,2. «Мир», Москва 19X8.
|
|
|
Ф. Дж. Мак-Вильяме и Н. Дж. Слоэн, Теория кодов, исправляющих ошибки, «Связь», Москва 1979.
Дж. Мэсси, Пороговое декодирование, «Мир», Москва 1966.
Дж. Проакис, Цифровая связь, Пер. с англ./Под ред. Д.Д. Кловского. - М.: Радио и связь. 2000. - 800 с: ил. ISBN 5-256-01434-Х
У. Питерсон и Э. Уэлдон, Коды, исправляющие ошибки, Пер. с англ./ Под ред. Р.Л.
Добрушина и С.Н. Самойленко. — МИР, Москва, 1976. -594 с: ил.
К. Шэннон, Работы по теории информации и кибернетике, «Иностранная литература», Москва 1963.
А.Д. Витерби и Дж. Омура, Принципы цифровой связи и кодирования, «Радио и связь», Москва 1982.
Дата добавления: 2018-02-18; просмотров: 1154; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
