Розділ 2. Молекулярна фізика і термодинаміка.

⇐ ПредыдущаяСтр 6 из 16Следующая ⇒

Основні формули.

1. Рівняння стану ідеального газу:

(для одного моля газу)

(для довільної маси газу),

де P– тиск, V- об’єм, Т – термодинамічна температура, m– маса, М – молярна маса, R– універсальна газова стала.

2. Закон Дальтона для тиску суміші газів:

де P_i– парціальний тиск і-ої компоненти газу.

3. Молярна маса суміші газів:

де m– маса і-ої компоненти, n - кількість молів і-ої компоненти.

4. Концентрація молекул однорідної системи:

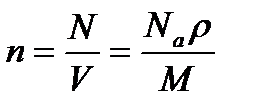де V – об’єм системи, r- густина речовини, N– число структурних елементів системи (молекул, атомів), N_a– число Авогадро.

5. Основне рівняння молекулярно-кінетичної теорії газів:

або:

де v_сер.– середня квадратична швидкістьмолекул, m₀– маса одної молекули, N– число молекул в об’ємі газу V, n– концентрація молекул.

6. Швидкість молекул:

- найбільш ймовірна: ;

- середня квадратична: ;

середня арифметична: .

7.Середня кінетична енергія поступального руху молекули ідеального газу:

8.Середня кінетична енергія однієї молекули:

де і – число степенів свободи молекули.

9. Перший закон термодинаміки:

де dQ– кількість теплоти, отриманої тілом, dU– зміна внутрішньої енергії, dA – робота, виконана тілом.

Молярна теплоємність:

де n - кількість молей (кількість речовини).

10. Молярна теплоємність газів, що складаються із n компонентів:

11. Питома теплоємність:

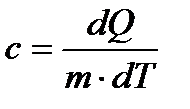
12. Внутрішня енергія ідеального газу:

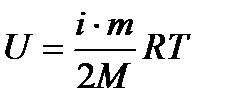
Приклади розв’язування задач.

Задача 2.1. Газ міститься в балоні ємністю V =75 л при температурі T=320 К і тиску P=2×10 Па. Знайти кількість молекул N в балоні, а також їх концентрацію n.

V=75 л,

T=320 К,

P=2×10 Па

N-?, n-?

Розв’язок.

Концентрація молекул n:

= .

Загальна кількість молекул:

=3,4×10

Відповідь. N=4,5×10²⁵ м^-3, N=3,4×10²⁴.

Задача 2.2В балоні місткістю V=10 л знаходиться гелій під тиском P₁=1 Мпа при температурі T₁=300 К. Після того, як із балону було взято Dm=10 г гелію, температура газу стaла дорівнювати T₂=290 К. Визначити тиск газу P₂, що залишився в балоні.

Дано:

V=10 л

P₁=1 Мпа

T₁=300 К

Dm=10 г

T₂=290 К

P₂-?

Розв’язок.

Запишемо рівняння Менделєєва-Клапейрона для початкового і кінцевого станів газу:

, .

З цих рівнянь, враховуючи, що , знаходимо:

звідки:

Масу знайдемо із рівняння для початкового стану:

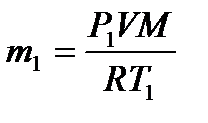Після перетворень одержуємо:

=3,64×10⁵ Па.

Відповідь. Р₂=3,64×10⁵ Па.

Задача 2. 3. Знайти середню арифметичну швидкість молекул газуv_ар., якщо відомо, що середня квадратична швидкість дорівнює v_кв.=100 км/с.

Дано:

v_кв.=100 км/с

v_ар.-?

Розв’язок.

Середня квадратична v_кв. і середня арифметична швидкості v_ар.Визначаються за наступними співвідношеннями:

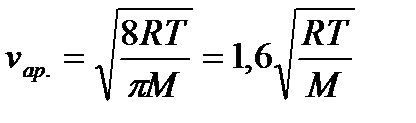Розділивши один цих виразів на інший, одержимо:

звідки

=925 м/с.

Відповідь.V_ар.=925 м/с.

Задача 2. 4.Знайти концентрацію водню n в балоні, якщо він знаходиться під тиском Р=2,7×10⁵ Па, а середня квадратична швидкість дорівнює v_кв.=2400 м/с.

Дано:

Р=2,7×10⁵ Па

v_кв =2400 м/с

n-?

Розв’язок.

Концентрація молекул пов’язана із тиском формулою:

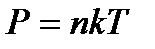звідки:

Невідому температуру знайдемо із виразу для середньої квадратичної швидкості:

, .

Підставивши цей вираз для температури у формулу для концентрації, одержуємо:

=4,2×10²⁵ м^-3.

Відповідь. N=4,2×10²⁵ м^-3.

Задача 2. 6.В балоні міститься m=140 г азоту при температурі T₁=300 К під тиском P₁=10⁵ Па. Після ізохорного нагрівання тиск збільшився в n=5 разів. Знайти об’єм балона V, кінцеву температуру Т₁ та кількість тепла DQ, що одержав газ.

Дано:

M=140 г

T₁=300 К

P₁=10⁵ Па

n=5

V - ?, Т₁ - ?, DQ-?

Розв’язок.

Об’єм балона визначимо із рівняння Менделєєва-Клапейрона для початкового стану газу:

, =1,24×10^-2 м³.

Кінцеву температуру визначимо із рівняння ізохорного процесу:

звідки:

=1500 К.

Тепло, що поглинув газ в ізохорному процесі:

=1,24×10⁴ Дж.

Відповідь. V=1,24×10^-2 м³, T₂=1500 К, DQ=1,24×10⁴ Дж.

Задача 2.7. Визначити температуру нагрівача T₁, якщо ідеальна теплова машина, що працює за циклом Карно, віддає холодильнику N=75% теплоти, що одержує від нагрівача. Температура холодильника T₂=300К.

Дано:

Q₂=0,75Q₁

T₂=300K

T₁– ?

Розв’язок.

Коефіцієнт корисної дії (ККД) теплової машини дорівнює:

h= ;

Для ідеального циклу Карно ККД становить:

Прирівняємо обидва значення ККД:

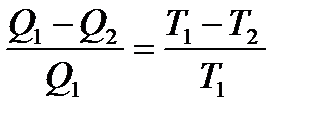, або .

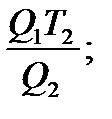; T₁= T₁= .

Відповідь: T₁=400K.

Задача 2.8.Коефіцієнт дифузії і в’язкості кисню за деяких умов дорівнюють D=1,22×10^-5 м/с і . Знайти густину кисню r, середню довжину вільного пробігу l і середню арифметичну швидкість v_сер. Його молекул.\

Дано:

D=1,22×10^-5 м/с

_________________________________________________________________

r - ?, l - ?, v_сер.- ?

Розв’язок.

Скористаємось формулами, які визначають коефіцієнт дифузії і динамічну в’язкість:

де ?, v_сер– середня арифметична швидкість; l- середня довжина вільного пробігу.

Звідси густина газу:

Середня довжина вільного пробігу

де d– діаметр молекул кисню, n – кількість молекул в одиниці об’єму.

Оскільки:

де Р– тиск газу, k– стала Больцмана, Т- температура кисню, то:

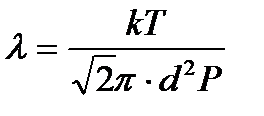Густина газу, згідно з рівнянням Менделєєва- Клапейрона:

=1,6 кг/м³.

Звідси:

В результаті:

=84 нм.

Середню арифметичну швидкість знайдемо з виразу для коефіцієнта дифузії з врахуванням виразу для середньої довжини вільного пробігу:

=437,7 м/с.

Відповідь. r=1,6 кг/м³, l=84 нм, v_сер.=437,7 м/с.

Задача 2.9. Нагрівник теплової машини, що працює за циклом Карно, має температуру Т₁=473 К. Яка температура холодильника Т₂, якщо за рахунок кожного кілоджоуля тепла, отримуваного від нагрівника, машина виконує роботу А=0,4 кДж?

Дано:

Т₁=473 К

А=0,4 кДж

_____________________________________________________________

Т₂ - ?

Розв’язок.

Температуру холодильника можна знайти, використавши вираз для К.К.Д. машини, яка працює за циклом Карно:

де Т - абсолютна температура нагрівника, Т - абсолютна температура холодильника.

Звідси:

К.К.Д. машини:

де А – корисна робота, виконана машиною; Q– тепло, яке підводиться до машини за той же час.

Тоді:

Т₂=283,8 К.

Відповідь. Т₂=283,8 К.

Задача2.10. Балон, що містить V₁=0,02м³повітря під тиском р₁=4·10⁵Па, сполучають з балоном місткістю V₂=0,06 м³, з якого викачане повітря. Знайти тиск р, який установився в посудинах. Температура стала.

Розв’язання:

Відповідь: р=10⁵ Па.

Задача 2.11 Скільки ртуті увійде в скляний балончик об’ємом 5 см³, нагрітий до t₁=400⁰C, при його охолодженні до t₂=16⁰C,якщо густина ртуті при t=16⁰Cдорівнює ?=13,6 г/см³?

Розв’язання:

Використаємо закон Гей-Люссака:

Складемо пропорцію:

Знайдемо, що

Тоді маса ртуті, яка ввійде в балончик, буде:

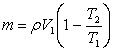
Підставивши числові значення, знайдемо:

Відповідь: т=0,4 г.

Задача 2.12 В балоні об’ємом V=10 лзнаходиться гелій під тиском р₁=1 Мпапри температурі Т₁=300 К.Після того, як з балона вийшло т=10 ггелію, температура в ньому зменшилась до Т₂=290 К. Визначити тиск гелію, який залишився в балоні.

Розв’язання:

де т₁ і т₂ – маси гелію в початковому і кінцевому стані.

З цих двох рівнянь виразимо маси:

Визначимо їх різницю:

Тоді тиск гелію в балоні буде визначатись за формулою:

Підставимо числові значення:

Відповідь: р₂=364 кПа.

Дата добавления: 2018-02-18; просмотров: 3544; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!