При решении ряда систем двух уравнений с двумя переменными можно применять теорему, обратную теореме Виета.
Например:
1. Решите систему уравнений 
Чаще всего эту систему решают способом подстановки. Но её можно решить более рациональным путём. Из условия следует, что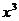 
и 
являются корнями некоторого приведенного квадратного уравнения 
. Корни этого уравнения 8 и -1.
Получаем: 
х = 2, у = -1.
или: 
х = -1, у = 2.
Ответ: (2; -1), (-1; 2).
2. Решите систему уравнений 
Возведем в куб обе части первого уравнения:
, 
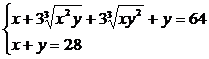
Используя теорему, обратную теореме Виета, получаем 
.
Корни этого уравнения 3 и 1.
х = 27, у = 1
или:
х = 1, у = 27
Ответ: (27; 1), (1; 27).
Этот метод можно применять при решении систем в тестах:
1. Решите систему уравнений 
Решение:
Из условия следует, что х и у2 являются корнями некоторого приведённого квадратного уравнения а2 -7а +12 =0. Корни этого уравнения 3 и 4. Получаем: х=3, у2=4, у=±2, или х=4, у2=3, у = ±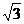 
.
А) (5; 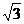), (5; - 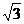), (3; 2), (3; -2).
В) (4; 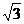), (4; - 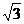), (3; 2), (3; -2).
С) (3; 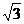), (3; - 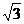), (3; 2), (3; -2).
D) (2; 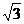), (2; - 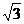), (3; 2), (3; -2).
Е) (5; 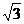), (3; - 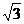), (3; 2), (3; -2).
(Вариант-23 №24 2003г.)
2. Решите систему уравнений 
А) (-1; 2), (2; -1).
В) (-1; 3), (1; -1).
С) (-2; 1), (-1; 2).
D) (2; 1), (-1; -2).
Е) (2; -1), (-1, 1).
(Вариант-8 №27 2003г.)
(Вариант-13 №26 2007г.)
(Вариант-25 №27 2006г.)
3. Решите систему уравнений 
Указание к решению: переходим к системе уравнений 
.
А) (1; 1).
В) (3; 5), (5; 3).
С) (15;3), (3;15).
D) (-3; -5), (-5; -3).
Е) нет решения.
(Вариант-13 №15 2004г.)
4. Решите систему уравнений 
|
|
|
А) (5; 1), (1; 5).
В) (2; 4), (4; 2).
С) (0; 6).
D) (3; 3).
Е) (6; 0).
(Вариант-25 №15 2004г.)
(Вариант-14 №20 2005г.)
5. Решите систему уравнений 
А) (2; 0).
В) (1; 1); ( 
.
С) (-1; 1).
D) (-1; 1); ( 
.
Е) (-1; 0).
(Вариант-21 №25 2005г.)
(Вариант-15 №26 2006г.)
Коды правильных ответов
| 1 | 2 | 3 | 4 | 5 |
| B | A | B | B | B |
При решении квадратных неравенств (и неравенств, сводящихся к ним), с которыми приходится часто иметь дело при подготовке к ЕНТ, удобно пользоваться свойством квадратного трехчлена 
, сформулированного следующим образом: «Если корни квадратного трехчлена действительные числа, то квадратный трехчлен имеет знак коэффициента при 
на всей числовой оси, за исключением замкнутого интервала между его корнями - 
, обращается в нуль в концах этого интервала, а внутри этого интервала знак квадратного трехчлена противоположен знаку коэффициента при ». Это свойство можно использовать при решении неравенств:
1. Решите неравенство: 5 
Решение: 5х2+9х-2=0, х1=-2, х2= 
. Так как квадратный трёхчлен имеет различные корни, то знак квадратного трёхчлена совпадает со знаком коэффициента а (а=5>0) во всех точках промежутков ( - 
; -2) и ( ; ), и противоположен знаку коэффициента а во всех точках промежутка ( -2; ).
|
|
|
Ответ: х 
(-2; ).
А) (-2; ).
В) ( ; 2).
С) (- ; 
).
D) (-2; 5) .
Е) (- ; ).
(Вариант-23 №8 2006г.)
2. Решите неравенство: 7 
А) (- ; - 
).
В) ( 
).
С) (- ; 
).
D) (- 
) .
Е) ( 
; ).
(Вариант-34 №8 2004г.)
3. Решите неравенство: 
А) (- ;3,2).
В) ( 
).
С) (- 
.
D) (- 
.
Е) (0; 3,2).
(Вариант-12 №8 2007г.)
4. Определите верное решение неравенства: 
Ответ: 
1 2 х
(Вариант-14 №18 2007г.)
5. Определите верное решение неравенства: 
.
А) [-2; 1].
В) [-1; 2].
С) 
.
D) 
.
Е) 
.
(Вариант-15 №18 2007г.)
6. Решите неравенство: 
А) (- ; -4) 
.
В) 
[ 
).
С) [-6; -4) (2; 4].
D) [-6;4].
Е) (-4; 2).
(Вариант-6 №18 2007г.)
7. Решите неравенство: 
.
А) нет решений.
В) [3; ).
С) (-1; 1 
.
D) [-1; 1 
.
Е) [-1; 3].
(Вариант-9 №18 2005г.)
8. Решите неравенство: 
.
А) 2.
В) 1\2.
С) (1; 6).
D) 
.
Е) 1.
(Вариант-12 №19 2005г.)
Коды правильных ответов
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| A | D | E | D | E | C | D | D |
III. Метод Крамера.
Системы линейных уравнений с двумя неизвестными можно решать методом подстановки, методом сложения, а можно применять метод Крамера или метод определителей. Учащимся, интересующимся математикой, этот метод нравится, и они его используют при подготовке к ЕНТ.
некоторые числа
, 
По коэффициентам системы составляются три определителя:
|
|
|
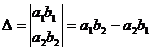
1) Если 
, а 
или 
, то система не имеет решений.
2) Если 
, то система имеет бесконечное множество решений.
3) Если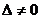 
, то система имеет единственное решение: 
.
Например:
Решите систему уравнений 
= -10 + 42 = 32
= 72 - 8 = 64
, у = 
Ответ: (-1; -2).
Этим методом можно решить системы:
1. Решите систему уравнений: 
А) (-1; 0).
В) (2; 3).
С) (-2; -1).
D) (6; 7).
Е) (4; 5).
(Вариант-19 №5 2003г.)
2. Решите систему уравнений: 
Указание к решению: от данной системы переходим к системе 
.
А) (3; 3).
В) (7; 8).
С) (-3; -1).
D) (-3; -3).
Е) (-1; 3).
(Вариант-26 №24 2003г.)
3. Решите систему уравнений: 
А) (-13; -5).
В) (-1; -3).
С) (-7; -4).
D) (5; -2).
Е) (11; -1).
(Вариант-19, №15, 2004г.)
4. Решите систему уравнений: 
А) (-3; 5).
В) (5; 3).
С) (-5; -3).
D) (3; 5).
Е) (3; -5).
(Вариант-24, №15, 2004г.)
5. Решите систему уравнений: 
А) (-5; -3).
В) (-3; 5).
С) (5; 3).
D) (3; 5).
Е) (3; -5).
(Вариант-2, №6, 2005г.)
6. Решите систему уравнений: 
А) (2; -7).
В) (7; 2).
С) (5; 0).
D) (0; 4).
Е) (4; -5).
(Вариант-26, №6, 2005г.)
7. Решите систему уравнений: 
А) (1; 7).
В) (-6; 0).
С) (5; 3).
D) (0; 6).
Е) (-5; 3).
(Вариант-23, №19, 2007г.)
8. Решите систему уравнений:
А) (2; 4).
В) (1\6; 0).
С) (-2; -1).
D) (4; 2).
Е) (-1; -2).
(Вариант-15, №14, 2004г.)
|
|
|
Коды правильных ответов
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| B | A | D | D | A | E | C | E |
IV. Использование геометрического смысла модуля при решении уравнений и неравенств, содержащих знак модуля.
При решении простейших неравенств, уравнений, содержащих неизвестное под знаком модуля, можно использовать геометрический смысл модуля.
Абсолютную величину (модуль) действительного числа х, т.е. |x|, можно геометрически истолковать, как расстояние от точки, изображающей число х, до начала отсчета; |x - а| означает расстояние между точками х и а на числовой прямой.
Например, если |x| = 3, то на числовой оси имеются только две точки 
которые удалены от начала отсчёта 0 на расстояние, равное трем.
-3 0 3
х
Примеры:
1. Решите уравнение: |x - 1| = 3.
Уравнению удовлетворяют такие точки х, расстояние которых от 1 на числовой прямой равно трём.
-2 1 4
х
Это точки -2 и 4.
Ответ: 
.
(Вариант-23 №6 2005г.)
2. Решите уравнение: |2x - 3| = 5. разделим обе части уравнения на 2:
|x – 1,5| = 2,5
От точки 1,5 отложим влево и вправо 2,5 единицы, получим точки 4 и – 1.
-1 1,5 4
х
Ответ: 
.
3. Решите неравенство: |х - 3| < 1.
Геометрический способ решения.
Неравенству удовлетворяют такие точки, которые удалены от точки 3 на расстояние, меньшее 1. От точки 3 отложим влево и вправо единицу, получим две точки: 2 и 4.
2 3 4
х
Точки, расстояние до которых от точки 3 меньше единицы, находятся внутри интервала (2;4). 2 и 4 в решение не входят, т.к. неравенство строгое. Поэтому, решением будет интервал (2;4).
Ответ: х (2; 4)
4. Решите неравенство: |2х + 3| < 5.
Разделим обе части неравенства на 2: 
< 
или |x – (- 
)| < .
От точки - откладываем влево и вправо. Получаем точки -4 и 1.
-4 -3/2 1
х
И таким образом получаем решение (-4; 1).
Ответ: (-4; 1).
5. Решите неравенство: |2х - 3| > 7.
Разделим обе части неравенства на 2: |x – 1,5| > 3,5
От точки 1,5 отложим влево и вправо 3,5 единиц. Получаем точки -2 и 5. точки, удалённые от 1,5 на расстояние, большее 3,5 единицам, расположены левее -2 и правее 5. Поэтому, решением неравенства будет объединение интервалов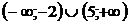 
. Т.к. неравенство строгое, -2 и 5 не принадлежат данным промежуткам.
-2 1,5 5
х
Ответ: .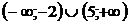
Геометрический способ решения можно применить при решении следующих заданий:
1. Решите уравнение: |2x - 3| = 6.
А) (- 
).
В) (-4.5; 4.5).
С) (-4.5; 1.5).
D) (- 
).
Е) (-1.5; 4.5).
(Вариант-18 №20 2005г.)
2. Определите верный промежуток-решение неравенства: |2x - 3| < 5.
(Вариант-16 №20 2005г.)
3. Решите уравнение: |2x - 3| = 1.
А) {2; -1}.
В) {-2; -1}.
С) {2; 1}.
D) {-2; 1}.
Е) {-3; 1}.
(Вариант-3 №12 2005г.)
4. Решите неравенство: |3х - 1| 
.
А) -1\3 
.
В) -3 
.
С) все ответы неверны.
D) -1 
.
Е) -1\2 .
(Вариант-34 №18 2007г.)
5. Определите верное решение неравенства: |x - 1| 
А) [4; 6].
В) (- ; 4].
С) [-6; 4].
D) (- ; -4].
Е) [-4; 6].
(Вариант-23 №8 2007г.)
6. Определите верное решение неравенства: |x + 2| 
А) [0; + ).
В) (- ; 0) 
).
С) [-4; 0].
D) (- ; -4].
Е) [- ; -4] 
(Вариант-22 №8 2007г.)
7. Определите верное решение неравенства: |1 + 2x| > 1.
А) (0;1).
В) (- ; -1) 
).
С) (- ; 0) 
).
D) (-1; + ).
Е) (-1; 0)
(Вариант-16 №19 2007г.)
8. Решите неравенство: |х| 
1.
А) (1; + ).
В) (- ; -1).
С) (0; + ).
D) (-1; 1).
Е) (- ; -1] [1; + ).
(Вариант-5 №7 2007г.)
9. Определите верный промежуток-решение неравенства: |3 + x| 
(Вариант-14 №7 2004г.)
10. Решите уравнение: |x - 1| =3.
A) {4; -2}.
B) {-1; 4}.
C) {2; -4}.
D) {-4; 3}.
E) {0; -3}.
(Вариант-17 №4 2004г.)
11. Определите верный промежуток-решение неравенства: |2x - 3| < 5.
(Вариант-23 №8 2004г.)
12. Решите систему уравнений: 
А) (0; 5),(-2;8).
В) (-1; 3), (7; -1).
С) (-1; -3), (-5; 1).
D) (1; -3), (-5; -1).
Е) (-1; 0) (5; 0).
(Вариант-11 №25 2006г.)
13. Решите неравенство: 2|х - 1| 
.
А) [-8; 9].
В) (- 
.
С) [-7; 9].
D) (- 
.
Е) [9; + 
.
(Вариант-19 №4 2003г.)
14. Решите неравенство: |х| <3.
А) (3; + ).
В) (- ; -3) 
.
С) (-3; 3).
D) (-3; 3].
Е) (- ; 3).
(Вариант-21 №4 2003г.)
Коды правильных ответов
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| E | C | C | A | E | E | B | E | E | A | E | B | C | C |
V. Тригонометрия на ладони. Решение тригонометрических уравнений.
Для решения некоторых тригонометрических примеров вовсе не обязательно пользоваться формулами. Можно использовать прямоугольный треугольник и четко знать определения синуса, косинуса, тангенса, котангенса.
Например:
1. tg 
= 8\15, 
.
Найти sin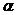 
.
Используем определение синуса острого угла прямоугольного треугольника , что это есть отношение противолежащего катета к гипотенузе, а так же, что синус в третьей четверти отрицательный, получаем: sin = -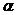 
.
2. cos 
, 
.
Найти: 
.
Учитывая определение синуса и тангенса, четверть, в которой лежит угол β, находим: 
.
3. Найти sin (arcos 2\3).
Применяем формулы:
, 
.
sin(arccos 
) = 
.
4. Вычислите: sin (2arccos a)
Пусть arcсos a равен , тогда sin 2 = 2 sin cos .
Найдем значения sin , cos и, подставив их в формулу, вычислим.
5. Вычислите: cos (2arcsin a)
Пусть arcsin a равен , тогда cos 2 = 
.
Найдем значения sin , cos и, подставив их в формулу, вычислим.
При решении заданий такого вида важно помнить следующие тождества:
А. 
| 
|
| 
|
| 
|
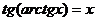
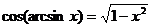
Б. 
| 
|
В. 
| 
|
Г. 
| 
|
| 
|
Аналогичные задания:
1. Вычислите: cos(2arcsin 
).
А) 1.
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-17 №26 2005г.)
2. Вычислите tg , если cos 
, 0 < < 
.
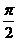А) 
.
В) 
.
С)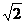 
.
D) 
.
Е) 
.
(Вариант-15 №7 2005г.)
3. Вычислите 3ctg 
, если sin 
0 < 
А) 3.
В) 2.
С) -2.
D) 4.
Е) 5.
(Вариант-20 №10 2007г.)
4. Вычислите: cos2 , если sin 
.
А) 
.
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-12 №9 2007г.)
5. Вычислите: 2 
, если sin 
, 0 
А) 1.
В) 3.
С) 2.
D) 7.
Е) 4.
(Вариант-27 №9 2004г.)
6. Вычислите: sin(2arccos3\5).
А) 0.96.
В) 0.98.
С) 1.
D) 0.97.
Е) 0.99.
(Вариант-32 №28 2006г.)
7. Чему равен cos a, если sin 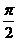a = , < a < 
?
А) 
.
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-13 №11 2003г.)
8. Вычислите cos 2a, если sin a = 
.
А) 
.
В) 
.
С) 
.
D) - .
Е) 
.
(Вариант-15 №5 2003г.)
9. Вычислите 4ctg a, если cos a = и 
.
А) -3,6.
В) 9,6.
С) 0.
D) -9,6.
Е) 1,6.
(Вариант-24 №28 2003г.)
Коды правильных ответов
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| D | A | D | E | B | A | B | C | D |
Тригонометрия – один из важнейших разделов математики. Чтобы успешно решать тригонометрические уравнения, упрощать тригонометрические выражения, нужно знать основные формулы тригонометрии и значения синуса, косинуса, тангенса, котангенса табличных углов. В одном из журналов «Математика» указан необычный способ, который можно применить для запоминания значений синусов и косинусов табличных углов. Это, конечно, мнемоническое правило, но в трудную минуту, например, на ЕНТ, оно может помочь.
Оказывается, значения синусов и косинусов углов «находятся» на нашей ладони. Рассмотрим правило нахождения синусов:
На пересечении продолжений мизинца и большого пальца находится бугор Луны. Измерим углы между пальцами (пальцы развести как можно сильнее). Угол между мизинцем и безымянным пальцем - 30º, угол между мизинцем и средним пальцем - 45º,угол между мизинцем и указательным пальцем - 60º, угол между мизинцем и большим пальцем - 90º. И это у всех людей без исключения. Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить пальцы с мизинцем, угол между лучами будет 0º, т.е. можно считать, что направление мизинца соответствует началу отсчета углов, т.е. 0º. Введем нумерацию пальцев:
Мизинец – №0 соответствует 0º;
Безымянный - №1 соответствует 30º;
Средний - №2 соответствует 45º;
Указательный - №3 соответствует 60º;
|
Нужно запомнить формулу: - половина квадратного корня из номера (n) пальца.
| Номер пальца | Угол
| Значение синуса |
| 0 | 0º | sin0º = 
|
| 1 | 30º | sin30º = 
|
| 2 | 45º | sin45º = 
|
| 3 | 60º | sin60º = 
|
| 4 | 90º | sin90º = 
|
а и большого пальца находится бугор Луны.
Для определения косинуса угла пальцы пронумеровать с большого, а начало отсчета углов оставить по-прежнему от мизинца.
При решении тригонометрических уравнений и неравенств видаsin
, чтобы получить ответ, данный в тестах, нужно решать, используя формулы понижения степени: 
Например:
Решите уравнение: sin 
.
I cпособ решения:
sin ,
sin 
; sin 
;
= (-1) 
= (-1) 
Объединяя решения, получаем ответ, данный в тестах: х = 
Но если использовать формулу 
, то получим сразу данный ответ. Этот способ решения для учащихся проще, т.к. нахождение объединения решений вызывает у них затруднения.
II cпособ решения:
sin , 
, 
, 
, 2x = 
x = 
Аналогичный способ решения можно применить в следующих заданиях:
1. Решите уравнение: sin 
.
Решение:
, 
, 
, 
, 
, 
, .
А) 
В) 
С) 
D) 
Е) 
(Вариант-35 №25 2005г.)
2. Решите уравнение: cos .
А) 
.
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-16 №30 2005г.)
3. Решите уравнение: sin 
3cos 
.
А) 
.
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-2 №5 2004г.)
4. Решите уравнение: 
А) 
.
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-5 №5 2004г.)
5. Решите неравенство: 3 – 4 соs 
А) ( 
.
В) ( 
.
С) ( 
.
D) ( 
.
Е) ( 
.
(Вариант-7 №9 2004г.)
(Вариант-35 №8 2004г.)
Коды правильных ответов
| 1 | 2 | 3 | 4 | 5 |
| D | E | A | E | D |
При решении тригонометрических уравнений, неравенств, упрощении тригонометрических выражений можно использовать правило:
Увидел сумму – преобразуй в произведение.
Дата добавления: 2018-02-18; просмотров: 817; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!