Вычисление статических моментов и координат центров тяжести плоских фигур.
Приложения интегрального исчисления к решению физических задач
Вычисление статических моментов и координат центра тяжести материальной кривой.
а) Пусть материальная точка A массы m отстоит от оси l на расстоянии d. Статистическим моментом этой точки относительно оси l называют число md. Статистическим моментом системы материальных точек  расположенных по одну сторону от оси l, массы которых равны
расположенных по одну сторону от оси l, массы которых равны  , а расстояния от оси l равны
, а расстояния от оси l равны  , называют число:
, называют число:
 =
=  .
.
Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси - отрицательными.
Поэтому если точки  расположены на координатной плоскости,
расположены на координатной плоскости,  =
=  (
(  ), то
), то  =
=  и
и  =
=  (
(  - статистический момент относительно оси Ox;
- статистический момент относительно оси Ox;  - относительно оси Oy).
- относительно оси Oy).
б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой Г или по некоторой области  . Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области - ее площади.
. Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области - ее площади.
Начнем со случая кривой линии Г, задаваемой уравнением 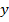 =
=  ,
,  , причем предположим, что функция
, причем предположим, что функция  непрерывна и неотрицательна.
непрерывна и неотрицательна.
Как обычно, разобьем отрезок  на части точками a=
на части точками a=  ...
...  =b и обозначим через
=b и обозначим через  и
и  наименьшее и наибольшее значения функции
наименьшее и наибольшее значения функции 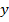 =
=  на отрезке [
на отрезке [  . Этому разбиению соответствует разбиение дуги Г на части
. Этому разбиению соответствует разбиение дуги Г на части  (рис. 60).
(рис. 60).
|
|
|

Из физических соображений ясно, что статистический момент  части
части  относительно оси абсцисс заключен между
относительно оси абсцисс заключен между  и
и  , где
, где  - длина этой части,
- длина этой части,  =
=  (напомним, что мы положили линейную плотность дуги равной единице).
(напомним, что мы положили линейную плотность дуги равной единице).
Таким образом,:
 .
.
Поэтому:
 , т.е.:
, т.е.:
 .
.
Так как на отрезке [  ;
;  ] выполняется неравенство:
] выполняется неравенство:  , то в тех же границах, что и
, то в тех же границах, что и  , заключен интеграл
, заключен интеграл  .
.
Значит,:
 =
=  (1)
(1)
Этот интеграл обозначают также следующим образом:
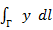 или
или  .
.
Физики обычно заменяют проведенное рассуждение более коротким. Они берут "бесконечно малый участок дуги" dl. Его статистический момент равен ydl. А статистический момент всей дуги равен сумме элементарных статистических моментов, т.е.  . Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое "бесконечно малый участок дуги", или как еще говорят, "элемент дуги". При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что:
. Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое "бесконечно малый участок дуги", или как еще говорят, "элемент дуги". При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что:
 =
=  =
=  . (2)
. (2)
|
|
|
Как формула (1), так и формула (2) верны и в случае, когда кривая Г пересекает оси координат.
в) Введем понятие центра тяжести.
Определение. Центром тяжести тела называется такая точка С, что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.
Обозначим через  и
и  расстояния центра тяжести кривой от осей ординат и абсцисс.
расстояния центра тяжести кривой от осей ординат и абсцисс.
Тогда, пользуясь определением центра тяжести кривой, получим:
 =l
=l  =
=  ;
;  =
=  =
=  .
.
Разрешая полученные равенства относительно  и
и  , найдем координаты центра тяжести плоской кривой Г:
, найдем координаты центра тяжести плоской кривой Г:
 =
=  ;
;  =
=  .
.
Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.
Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.
Пример 1. Найдем статический момент полуокружности относительно диаметра.
Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью Ox. Тогда статический момент полуокружности относительно диаметра выразится формулой:
|
|
|
 =
=  , где dl=
, где dl=  dx - дифференциал дуги кривой y=
dx - дифференциал дуги кривой y=  .
.
В выбранной системе координат уравнение полуокружности запишется так:
y=  .
.
Тогда:
y'=-  , 1+
, 1+  =1+
=1+  =
=  ,и потому dl=
,и потому dl=  .
.
Следовательно,:
 =
=  =2R
=2R  =2Rx|
=2Rx|  =2
=2  .
.
Пример 2. Найдем центр тяжести четверти окружности  +
+  =4, расположенной в первом квадранте.
=4, расположенной в первом квадранте.
Решение. Данная кривая расположена симметрично относительно биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому  =
=  .
.
Достаточно найти только  , пользуясь формулой:
, пользуясь формулой:
 =
= 
Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:
 .
.
Отсюда находим, что:
 =-2
=-2  ,
, 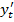 =
=  ,
,
dl=  =
=  =2dt.
=2dt.
Поскольку длина l четверти данной окружности равна  =
=  , то:
, то:
 =
=  =
=  =
=  .
.
Вычисление статических моментов и координат центров тяжести плоских фигур.
Найдем статический момент прямоугольника со сторонами k и l относительно стороны k. Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны k и dy (рис. 61). Масса элементарного прямоугольника равна его площади kdy (напоминаем, что по предложению плотность распределения массы равна единице). Поэтому элементарный статический момент равен ky dy, а статический момент всего прямоугольника равен:
|
|
|
 =
=  =
=  . (1)
. (1)

Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой 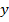 =
=  , где
, где  - непрерывная и неотрицательная функция на отрезке [a;b], снизу осью абсцисс, а с боков прямыми x=a, x=b.
- непрерывная и неотрицательная функция на отрезке [a;b], снизу осью абсцисс, а с боков прямыми x=a, x=b.
Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно dx и высота y. Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен  . В случае когда не выполняется предположение о не отрицательности функции y=
. В случае когда не выполняется предположение о не отрицательности функции y=  , эту формулу надо заменить такой:
, эту формулу надо заменить такой:
 =
=  - (части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в
- (части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в  ).
).
Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т.е. интегралу  , а потому ордината центра тяжести этой трапеции выражается формулой:
, а потому ордината центра тяжести этой трапеции выражается формулой:
 =
=  .
.
Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно x. Поэтому его статический момент равен x|y|dx, а статический момент всей трапеции выражается формулой:
 =
=  .
.
Следовательно, абсцисса центра тяжести выражается так:
 =
=  .
.
Пример 3. Найдем статический момент (относительно оси Ox) фигуры, ограниченной осью абсцисс и одной аркой циклоиды: x=  -
- 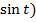 , y=
, y=  -
-  .
.
Решение. Так как параметр t одной арки циклоиды изменяется от 0 до 2  , то:
, то:
 =
= 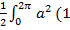 -
-  -
-  =
=  -
-  =
= 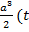 -3
-3  +
+  +
+ 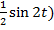 -(
-(  -
-  ))|
))|  =
=  +
+  =
=  .
.
Пример 4. Найдем центр тяжести фигуры, ограниченной осью Ox и одной полуволной синусоиды y=  .
.
Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой x=  , то центр тяжести лежит на этой прямой и, следовательно,
, то центр тяжести лежит на этой прямой и, следовательно,  =
=  . Ордината
. Ордината  центра тяжести находится по формуле:
центра тяжести находится по формуле:
 =
=  .
.
Так как:
 =
=  =-
=-  =2, то
=2, то  =
=  =
=  .
.
Итак, центр тяжести данной фигуры находится в точке ( 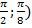 .
.
Пример 5. Найдем центр тяжести фигуры, ограниченной осью абсцисс и одной циклоиды x=  -
- 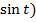 , y=
, y=  -
-  .
.
Решение. Данная фигура расположена симметрично относительно прямой x=  , следовательно, центр тяжести ее находится на этой прямой, и потому
, следовательно, центр тяжести ее находится на этой прямой, и потому  =
=  . Найдем
. Найдем  по формуле:
по формуле:
 =
=  .
.
Площадь S данной фигуры была вычислена раньше, она равна 3  . Следовательно,
. Следовательно,  =
=  -
-  =
=  .
.
Центр тяжести данной фигуры находится в точке (  .
.
Теорема Гульдина-Паппа.
Выведем теоремы, связывающие площадь поверхности (соответственно, объем тела) вращения с центром тяжести вращающейся дуги (соответственно, криволинейной трапеции).
Пусть поверхность  образована вращением дуги Г, имеющей длину l. Мы знаем, что ордината центра тяжести этой дуги выражается формулой:
образована вращением дуги Г, имеющей длину l. Мы знаем, что ордината центра тяжести этой дуги выражается формулой:
 =
=  .
.
Так как площадь поверхности вращения выражается интегралом:
 =2
=2  , из этого следует, что:
, из этого следует, что:  =2
=2  .
.
Мы доказали следующее утверждение, называемое первой теорией Гульдина-Паппа.
Площадь поверхности, полученной от вращения кривой вокруг непересекающей ее оси, равна произведению длины l дуги этой кривой на длину окружности, описанной центром тяжести C этой кривой.
Аналогично, из формулы, выражающей ординату центра тяжести криволинейной трапеции:
 =
=  и формулы объема тела вращения:
и формулы объема тела вращения:  =
=  - получаем
- получаем  =
=  , т.е. следующее утверждение, называемое второй теоремой Гульдина-Паппа:
, т.е. следующее утверждение, называемое второй теоремой Гульдина-Паппа:
Объем тела, полученного от вращения плоской фигуры вокруг непересекающей ее оси, равен произведению площади этой фигуры на длину окружности, описанной центром тяжести этой фигуры.
Пользуясь этими двумя теоремами, можно в ряде случаев упростить процесс вычисления поверхности или объема тела вращения.
Пример 6. Пользуясь теоремой Гульдина-Паппа, вычислим площадь поверхности и объема тора (рис. 62), образованного вращением круга радиуса a вокруг оси, расположенной в его плоскости и отстоящей от центра его на расстоянии b (a  b).
b).

Решение. Так как длина данной окружности равна 2  , а длина окружности, описанной центром тяжести ее, равна 2
, а длина окружности, описанной центром тяжести ее, равна 2  , то поверхность тора по первой теореме Гульдина-Паппа равна:
, то поверхность тора по первой теореме Гульдина-Паппа равна:
 =
=  =
=  .
.
Объем тора равен:  =
=  =
=  .
.
Пример 7. Длина одной арки циклоиды  =
=  -
-  ),
), 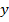 =
=  -
-  равна
равна  , а площадь поверхности, образованной вращением ее вокруг оси Ox, равна
, а площадь поверхности, образованной вращением ее вокруг оси Ox, равна  . Вычислим площадь поверхности, образованной вращением той же арки циклоиды вокруг касательной в верхней ее точке (рис. 63).
. Вычислим площадь поверхности, образованной вращением той же арки циклоиды вокруг касательной в верхней ее точке (рис. 63).

Решение. Пусть  - расстояние центра тяжести дуги от оси Ox, тогда по первой теореме Гульдина-Паппа:
- расстояние центра тяжести дуги от оси Ox, тогда по первой теореме Гульдина-Паппа:  =
=  , откуда:
, откуда:  =
=  .
.
наибольшая ордината кривой соответствует  =
=  и равна 2
и равна 2  , причем касательная в этой точке параллельна оси Ox; следовательно, расстояние h центра тяжести этой касательной равно:
, причем касательная в этой точке параллельна оси Ox; следовательно, расстояние h центра тяжести этой касательной равно:  -
-  =
=  .
.
Таким образом, площадь поверхности, образованной вращением той же арки циклоиды вокруг касательной в верхней ее точке, равна:  =
=  =
=  .
.
Пример 8. Найдем объем тела, полученного от вращения квадрата со стороной a вокруг оси Ox, если он расположен так, как показано на рисунке 64.

Решение. Центр тяжести C квадрата находится на пересечении его диагоналей. Обозначим через b расстояние центра тяжести Ox. Тогда по второй теореме Гульдина-Паппа искомый объем:
 =
=  =2
=2  .
.
Вычисление моментов инерции.
Моментом инерции материальной точки A относительно оси l называется число  , где
, где  - масса точки, а d - ее расстояние от оси. Аналогично определяется момент инерции относительно точки.
- масса точки, а d - ее расстояние от оси. Аналогично определяется момент инерции относительно точки.
Пусть Г - материальная линия, линейная плотность которой во всех точках равна единице. Тогда масса элементарного участка этой линии равна его длине dl, а момент инерции  такого участка относительно оси абсцисс равен
такого участка относительно оси абсцисс равен  . Интегрируя, получаем момент инерции относительно оси абсцисс всей линии:
. Интегрируя, получаем момент инерции относительно оси абсцисс всей линии:  =
=  .
.
Так же доказывается, что:  =
=  и
и  =
=  +
+  , где
, где  - момент инерции относительно начала координат.
- момент инерции относительно начала координат.
Отсюда следует, в частности, что  =
=  +
+  .
.
Есть линия Г задана параметрическими уравнениями:  =
=  ,
, 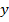 =
=  , 0
, 0  , то
, то  =
=  .
.
Аналогичные формулы справедливы для  и
и  .
.
Перейдем к вычислению моментов инерции криволинейной трапеции. Будем считать, что ее поверхностная плотность равна единице. Сначала найдем момент инерции прямоугольника со сторонами k и l относительно стороны k. Разобьем его на элементарные прямоугольники со сторонами k и dy (см. рис. 61). Площадь (а потому и масса) каждого такого прямоугольника равна kdy. Значит, момент инерции элементарного прямоугольника относительно этой стороны выражается формулой:  =
=  =
=  .
.
Криволинейную трапецию разобьем на элементарные прямоугольники со сторонами |y| и dx. Момент инерции каждого из этих прямоугольников относительно оси абсцисс выражается формулой:  =
=  . Интегрируя, получаем момент инерции всей криволинейной трапеции относительно оси абсцисс:
. Интегрируя, получаем момент инерции всей криволинейной трапеции относительно оси абсцисс:
 =
=  .
.
Аналогично доказывается, что момент инерции криволинейной трапеции относительно оси ординат выражается формулой:
 =
=  - (момент инерции элементарного прямоугольника относительно оси ординат равен
- (момент инерции элементарного прямоугольника относительно оси ординат равен  ).
).
Полярный момент инерции (т.е. момент относительного начала координат) в этом случае выражается формулой:  =
=  +
+  .
.
Пример 9. Вычислим момент инерции равнобедренного треугольника относительно его основания.
Решение. Расположим оси координат так, как показано на рисунке 65.

Пусть основание треугольника |AC|=b, высота |BO|=h. Прямая (BC) проходит через точки B (0;h) и C (  ). Ее уравнение
). Ее уравнение 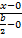 =
=  , т.е. y=
, т.е. y=  . Ясно, что момент инерции
. Ясно, что момент инерции  треугольника ABC относительно оси Ox равен удвоенному моменту инерции треугольника BOC относительно той же оси. Значит,:
треугольника ABC относительно оси Ox равен удвоенному моменту инерции треугольника BOC относительно той же оси. Значит,:  =
=  =
=  -
-  =
= 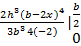 =
=  .
.
Дата добавления: 2018-02-18; просмотров: 2400; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
