Метод математической индукции.
Контрольные вопросы:
1. Натуральный ряд чисел. Аксиомы Пеано.
2. Основная форма метода математической индукции.
3. Обобщение основной формы метода математической индукции.
4. Вторая форма метода математической индукции.
5. Обобщение второй формы метода математической индукции.
6. Алгоритм доказательства утверждения методом математической индукции.
План занятия:
1. Проверка домашнего задания.
2. Решение типовых задач.
3. Самостоятельная работа
| Номер задания | Аудиторная работа | Домашняя работа |
| 1 | 1)-4) | 5)-8) |
Задание 1. Доказать, что для любого натурального числа  :
:
1) а) справедливо равенство  ;
;
б)  делится на
делится на  ;
;
2) а) справедливо равенство  ,
,
б)  делится на
делится на 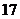 ;
;
3) а) справедливо равенство  ,
,
б)  делится на
делится на  ;
;
4) а) справедливо равенство 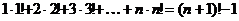 ,
,
б) 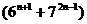 делится на
делится на  ;
;
5) а) справедливо равенство  ,
,
б)  делится на
делится на  ;
;
6) а) справедливо равенство 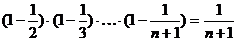 ,
,
б)  делится на
делится на  ;
;
7) а) справедливо равенство  ,
,
б) 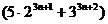 делится на
делится на  ;
;
8) а) справедливо равенство  ,
,
б)  делится на
делится на  .
.
Практическое занятие 11.
Обобщающее занятие по темам «Векторная алгебра»,
«Аналитическая геометрия»,
«Комплексные числа и метод математической индукции».
Вариант 0
1. В треугольнике ABC точка М – середина AB, N – середина ВС. Дано:  ,
,  . Найти
. Найти 
2. Даны векторы  ,
,  ,
,  =5,
=5,  =2,
=2,  . Вычислить проекцию вектора
. Вычислить проекцию вектора 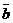 на вектор
на вектор  .
.
|
|
|
3. Найти площадь параллелограмма, построенного на векторах  ,
,  , если
, если  ,
,  =3,
=3,  .
.
4. Дано  =1,
=1,  =2,
=2,  . Вычислить
. Вычислить  .
.
5. Дано: А(1,2,3), В(-2,4,1), C(7,6,3) и D(4,-3,-1). Найти:
a) площадь треугольника ABC
b) косинус угла между векторами  .
.
6. Даны вершины треугольника ABC: A(-1;3), B(2;2), C(6;-3). Найти:1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) уравнение высоты CD и её длину; 4) уравнение медианы AE и координаты точки K пересечения этой медианы с высотой CD; 5) уравнение прямой, проходящей через точку К параллельно стороне AB; 6) координаты точки М, расположенной симметрично точке А относительно прямой CD.
7. Даны координаты вершин пирамиды  . Найти: 1) длину ребра
. Найти: 1) длину ребра  ; 2) угол между рёбрами
; 2) угол между рёбрами  и
и  ; 3) угол между рёбром
; 3) угол между рёбром  и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объём пирамиды; 6) уравнение прямой
; 5) объём пирамиды; 6) уравнение прямой  ; 7) уравнение плоскости
; 7) уравнение плоскости  ; 8) уравнение высоты, опущенной из вершины
; 8) уравнение высоты, опущенной из вершины  на грань
на грань  .
. 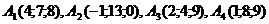 .
.
8. Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса  , а две другие совпадают с концами его малой оси.
, а две другие совпадают с концами его малой оси.
9. Доказать, что для любого натурального числа  справедливо:
справедливо:
a)  ;
;
b)  делится на
делится на  ;
;
10. Решить уравнение над ℂ: 
 .
.
|
|
|
11. Вычислить, используя тригонометрическую форму записи комплексного числа:  .
.
Практическое занятие 12.
Рубежная аттестация 1.
Дата добавления: 2018-02-18; просмотров: 450; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
