Различные способы задания прямой.

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Контрольные вопросы:

1. Прямоугольная система координат на плоскости.

2. Полярная система координат на плоскости.

3. Связь прямоугольных координат и полярных координат точки.

4. Расстояние между точками.

5. Параллельный перенос системы координат.

6. Поворот осей координат.

7. Линия на плоскости.

8. Уравнение линии на плоскости.

9. Уравнение прямой с угловым коэффициентом.

10. Общее уравнение прямой.

11. Уравнение прямой, проходящей через данную точку в данном направлении.

12. Уравнение прямой, проходящей через две данные точки.

13. Уравнение прямой в отрезках.

14. Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору.

15. Угол между прямыми.

16. Условие параллельности двух прямых.

17. Условие перпендикулярности двух прямых.

18. Расстояние от точки до прямой.

План занятия:

1. Теоретический диктант.

2. Решение типовых задач.

Номер задания	Аудиторная работа	Домашняя работа
1		+
2	+
3	+
4		+
5	+
6		+
7	1)	2)

Задание 1.Найти угловой коэффициент k прямой, проходящей через точки (1,8) и (–1,4); записать уравнение прямой в параметрическом виде.

Задание 2.Составить уравнения сторон и медиан треугольника с вершинами A(3,2), B(5,–2), C(1,0).

Задание 3.Даны вершины треугольника A(–10,–13), B(–2,3), C(2,1). Вычислить длину перпендикуляра, опущенного из вершины B на медиану, проведенную из вершины C.

Задание 4.Найти острый угол между прямой и прямой, проходящей через точки (–2,3) и (2,–3).

Задание 5.Составить уравнения сторон треугольника, зная одну его вершину C(4,–1), уравнение высоты и медианы , проведенных из одной вершины.

Задание 6.Найти расстояние между прямыми и .

Задание 7.Даны вершины треугольника ABC. Найти:1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) уравнение высоты CD и её длину; 4) уравнение медианы AE и координаты точки K пересечения этой медианы с высотой CD; 5) уравнение прямой, проходящей через точку К параллельно стороне AB; 6) координаты точки М, расположенной симметрично точке А относительно прямой CD.

1) A(4;3), B(-3;-3), C(2;7);

2) A(-3;-3), B(5;-7), C(7;7).

Практическое занятие 4.

Эллипс, гипербола, парабола.

Их свойства.

Контрольные вопросы:

1. Окружность.

2. Уравнение окружности с центром радиуса .

3. Понятие эллипса.

4. Каноническое уравнение эллипса.

5. Полуоси эллипса.

6. Эксцентриситет эллипса.

7. Фокальные радиусы эллипса.

8. Директриса эллипса.

9. Понятие гиперболы.

10. Каноническое уравнение гиперболы.

11. Центр гиперболы.

12. Вершины гиперболы.

13. Действительная и мнимая полуоси гиперболы.

14. Основной прямоугольник гиперболы.

15. Асимптоты гиперболы.

16. Равносторонняя гипербола.

17. Эксцентриситет гиперболы.

18. Фокальные радиусы гиперболы.

19. Директрисы гиперболы.

20. Сопряженные гиперболы.

Аудиторная работа	Домашняя работа
1),3),5),8),10),15),17,19),21)	2),4),6),7),9),11)-14),16),18),20),22),23)

21. Понятие параболы.

22. Каноническое уравнение параболы.

23. Фокус, директриса параболы.

24. Параметр параболы.

25. Ось симметрии параболы.

26. Вершина параболы.

27. Фокальный радиус.

План занятия:

1. Теоретический диктант.

2. Проверка домашнего задания.

3. Решение типовых задач.

Задание 1.Составить каноническое уравнение эллипса, проходящего через точки и .

Задание 2.Составить уравнение эллипса, если

1) его фокальное расстояние равно 10, а малая полуось равна 5;

2) его эксцентриситет равен , а большая полуось равна 3;

3) расстояние между фокусами равно 8, а эксцентриситет равен ;

4) прямые служат директрисами эллипса, а малая полуось равна 2;

5) расстояние между директрисами равно 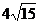, а эксцентриситет равен .

Задание 3.Написать каноническое уравнение эллипса, если его эксцентриситет равен , а большая полуось равна 6.

Задание 4.Написать уравнение эллипса, если расстояние между фокусами равно расстоянию между концами большой и малой осей. Определить эксцентриситет.

Задание 5.В эллипс вписан прямоугольник, две противоположные стороны которого проходят через фокусы эллипса. Вычислить площадь прямоугольника.

Задание 6.Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, если расстояние между фокусами равно 24, а эксцентриситет равен .

Задание 7.Через фокус эллипса проведен перпендикуляр к его большей оси. Определить расстояние от точек пересечения этого перпендикуляра с эллипсом до фокусов.

Задание 8.Через фокус эллипса провести прямую, перпендикулярно прямой .

Задание 9. Найти общие точки эллипса и прямой, проходящей через точку под углом к оси ординат.

Задание 10.Написать уравнение гиперболы, проходящей через фокусы эллипса и имеющей фокусы в вершинах этого эллипса.

Задание 11.Дана гипербола . Написать уравнение сопряженной с ней гиперболы; найти эксцентриситеты, директрисы и асимптоты данной и сопряженной гипербол.

Задание 12.Составить каноническое уравнение гиперболы, если угол между асимптотами равен и гипербола проходит через точку .

Задание 13.Составить каноническое уравнение гиперболы, имеющей общие фокусы с эллипсом и проходящей через точку .

Задание 14. Асимптоты гиперболы имеют уравнения , а расстояние между фокусами равно 20. Написать ее каноническое уравнение. Построить.

Задание 15.Дан эллипс . Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах данного эллипса. Построить эллипс и гиперболу.

Задание 16.Найти полуоси, координаты вершин и фокусов, эксцентриситет, уравнения директрис и асимптот гиперболы . Построить.

Задание 17.Составить уравнение прямой, проходящей через положительный фокус гиперболы 9x²-16y²=144 и составляющей с осью ординат угол, равный 30 .

Задание 18.Составить каноническое уравнение параболы, если

1) расстояние от фокуса, лежащего на оси , до вершины равно 4;

2) парабола симметрична относительно оси абсцисс и проходит через точку ;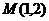

3) парабола симметрична относительно оси ординат и проходит через точку .

Задание 19.Составить каноническое уравнение параболы, если ее фокус находится в точке пересечения прямой с осью .

Задание 20.На параболе найти точку, фокальный радиус которой равен 4.

Задание 21.Написать уравнение окружности, проходящей через начало координат и точки пересечения параболы с осями координат.

Задание 22.Написать уравнение параболы, если она проходит через точки пересечения прямой и окружности и симметрична оси .

Задание 23.Составить уравнение параболы, если даны ее фокус F(4,3) и директриса . Построить параболу.

Практическое занятие 5.

Дата добавления: 2018-02-18; просмотров: 1125; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!