Задача аппроксимации в синтезе электрических цепей
Аппроксимация функций является одним из разделов математики и широко используется в различных областях знаний. В § 10.2 мы сталкивались с аппроксимацией В АХ нелинейных элементов. И в данном случае подход к решению задачи остается прежним. Прежде всего это касается критериев близости функций. Напомним, что наиболее распространенными являются два критерия. Во-первых, это среднеквадратический критерий, когда минимизируется интеграл от квадрата модуля разности функций. Другим критерием является минимаксный критерий, когда минимизируется максимум модуля разности двух функций. Если достигается такой минимум, то говорят, что аппроксимация выполнена по Чебышеву или оптимально равномерно. Однако в решении задачи аппроксимации при синтезе цепей имеются и отличия. Во-первых, существуют ограничения на вид аппроксимирующих функций и, во-вторых, должны контролироваться УФР.
Действительно, если выполняется аппроксимация квадрата модуля передаточной функции, то в качестве аппроксимирующей необходимо выбрать дробно-рациональную функцию, которая представляет собой отношение двух четных полиномов с вещественными коэффициентами. При этом степень полинома числителя не должна превышать степени полинома знаменателя и свободный член полинома знаменателя не может равняться нулю. Таким выбором аппроксимирующей функции удовлетворяются первые два УФР квадрата модуля передаточной функции. Третье условие должно контролироваться в процессе решения аппроксимационной задачи.
|
|
|
Когда рассматриваются временные характеристики, то выбору аппроксимирующей функции осуществляется в соответствии с выражениями (16.7).

Различные аппроксимации (приближения одной функции к другой) отличаются, прежде всего, понятиями «близости» двух функций. Наиболее широкое распространение в радиотехнике и связи получили такие методы аппроксимации, как интерполяция, приближение по Тейлору, приближение по Чебышеву, среднеквадратическое приближение.
При приближении функции F(x) и ζ(х) методом интерполяции наилучшей «близостью» этих функций считается совпадение их значений в выбранных точках — узлах интерполяции — х1, х2, ..., хN, т. е.

Решение этой системы уравнений позволяет найти искомые значения коэффициентов ось α1, α2 ,…αN.
Решение задачи аппроксимации данным методом (см. § 10.2) имеет следующие недостатки:
1. Отсутствует процедура выбора точек интерполяции и первоначального порядка функции и поэтому время, необходимое для отыскания оптимального решения, зависит от квалификации и интуиции разработчика.
|
|
|
2. В процессе решения не контролируются УФР.
Несмотря на отмеченные недостатки, метод интерполяции применяется довольно широко на практике, например, при синтезе амплитудных корректоров.
Данный метод аппроксимации применяется довольно часто ввиду его простоты, однако он не гарантирует получения физически реализуемой функции F(x).
Приближение функций по Тейлору предполагает, что наилучшая «близость» (Fx) и ζ(х) достигается при совпадении в выбранной точке x0 значений самих функций и их (N— 1) производных. Таким образом,

В основе этой системы уравнений лежит разложение функций F(x) и ζ(х) в ряды Тейлора и приравнивание первых N коэффициентов соответствующих рядов. Приближение по Тейлору нашло применение, в частности, при синтезе электрических фильтров. По имени автора, впервые предложившего такой вид аппроксимации в теории фильтров, она называется аппроксимацией по Баттерворту (см. § 7.2).
Наилучшее приближение функции F(x) к ζ(х) при аппроксимации по Чебышеву определяется из условия
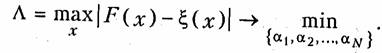
Этот критерий «близости» функций следует понимать так: коэффициенты α1, α2 ,…αN функции F(x) должны быть выбраны такими, чтобы самое наибольшее отклонение F(x) от ζ(х) в любой точке х рассматриваемого диапазона сделать минимально возможным.
|
|
|
Задача чебышевских приближений решена аналитически для электрических фильтров (см. § 17.2).
При использовании Чебышевского критерия близости полезной является теорема Чебышева, которая формулируется следующим образом.
Теорема Чебышева. Если рациональная функция F(x, α1, α2 ,…αN) с п коэффициентами аппроксимирует вещественную функцию на данном интервале по Чебышеву, то все максимумы отклонения равны между собой, а также равны величинам отклонений на границах интервала и достигаются не менее, чем в N + 1 точках, причем знаки отклонений чередуются.
Эта теорема отвечает на вопрос: данная аппроксимация выполнена оптимально или нет.
При среднеквадратическом приближении наилучшая «близость» двух функций достигается при выполнении условиям

т.е. при таких значениях коэффициентов α1, α2 ,…αN, при которых сумма квадратов отклонений F(x) от ζ(х) в точках х1, х2, ..., хM (M>N)является минимально возможной.
Минимизация достигается путем составления и решения системы алгебраических уравнений:

Отметим, что заданная и аппроксимирующие функции могут быть не только вещественными, но и комплексными, что позволяет одновременно аппроксимировать как АЧХ, так и ФЧХ.
|
|
|
При решении задач среднеквадратических приближений разработано большое количество численных методов, предназначенных для использования их на ЭВМ.
Заметим, что не существует четких рекомендаций по применению того или иного метода аппроксимации. Зачастую выбор метода зависит от сложности решения задачи аппроксимации (аналитического или численного), от конкретного применения синтезированной цепи и т. п.
44.(18) Фильтры Баттерворта. Если в выражениях, описывающих квадрат АЧХ фильтра (17.4) и его рабочее ослабление (17.5), в качестве функции фильтрации используются полиномы Баттерворта  (по имени автора, предложившего использовать их для «конструирования» частотных характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.
(по имени автора, предложившего использовать их для «конструирования» частотных характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.
Из формул (17.4) и (17.5) следует, что для фильтров Баттерворта на частоте Ω = 0 значение квадрата АЧХ равно единице, а рабочего ослабления — нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (17.4) и (17.5) приближенно воспроизводят характеристики идеального фильтра.
Чтобы эти характеристики «вписывались» в предъявляемые к фильтру требования (см. рис. 17.3), необходимо иметь рабочее ослабление (17.5) в полосе пропускания меньшее Артах, а в полосе непропускания большее Ар min. Первому условию можно удовлетворить, если потребовать на граничной частоте полосы пропускания (Ω = 1) выполнения равенства Ap(Ω)Ω=1= Артах или  Отсюда с учетом (17.5) или (17.4) имеем
Отсюда с учетом (17.5) или (17.4) имеем  Вычисленный таким способом коэффициент Е:
Вычисленный таким способом коэффициент Е:

называется коэффициентом неравномерности ослабления в полосе пропускания фильтра.
В формуле (17.6) величина Артах имеет размерность непер. Если воспользоваться значениями Артах в децибелах, то

С учетом введенных обозначений квадрат АЧХ фильтра Баттер-ворта запишется в виде

Эта функция удовлетворяет свойствам квадрата АЧХ реальных четырехполюсников, и поэтому ей можно сопоставить физически осуществимый электрический фильтр.
Рабочее ослабление фильтра Баттерворта:


Половина полюсов функции Нр(р)Нр(—р) лежит в левой полуплоскости комплексной переменной р и может быть отнесена к передаточной функции реализуемого фильтра Нр(р). Другая половина полюсов, являясь зеркальным отражением первой, располагается в правой полуплоскости и относится к Нр(—р).
Построенная из полюсов, лежащих в левой полуплоскости, передаточная функция фильтра Баттерворта является полиномиальной передаточной функцией типа (17.1):
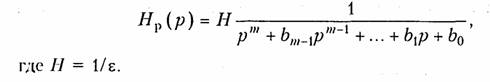

Используя введенное ранее обозначение Bm(Ω) = Ω'" полинома Баттерворта, можно представить частотные характеристики (17.8) и (17.9) фильтра Баттерворта в следующей форме:

Фильтры Баттерворта называют также фильтрами с максимально плоским ослаблением в полосе пропускания (см. рис. 17.4, а).
44. Полиномиальные фильтры Чебышева.Если в качестве функции фильтрации в (17.4) и (17.5) использовать полином Чебышева, обозначаемый 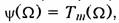 то формулы (17.14) примут вид:
то формулы (17.14) примут вид:


где Tm(Ω) — полином Чебышева степени (порядка) т; ε — коэффициент неравномерности, определяемый (17.6) или (17.7).
Фильтры с частотными характеристиками (17.15) называются фильтрами Чебышева. Проанализируем частотные характеристики фильтра Чебышева. Для этого вначале рассмотрим свойства полиномов Tm(Ω). Ниже приведены шесть первых полиномов Чебышева:

Анализ поведения полиномов Чебышева показывает, что в интервале —1 ≤Ω≤1 угол Θ = arccosΩ изменяется от —π (приΩ = —1) до 0 (при Ω = 1), поэтому полином Tm(Ω) = cosmΘровнот раз принимает значения, равные нулю, и т +1 раз достигает значений, равных +1 пли —1 и чередующихся друг с другом. Вне интервала —1 ≤Ω≤ 1 полином Тm(Ω) согласно формуле (17.16 в) монотонно возрастает.

В качестве примера на рис. 17.6, а изображен график полинома Чебышева T4(Ω), т. е. полинома четвертого порядка.
В соответствии с (17.15) рабочее ослабление Ар(Ω.) фильтра Чебышева на тех частотах Ω, где полином Тm(Ω) обращается в нуль, также обращается в нуль. На частотах, на которых Tm(Ω)равен ±1, рабочее ослабление достигает величины:

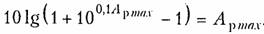
С ростом значений полинома Тm(Ω) на частотах Ω > 1 рабочее ослабление АР(Ω) также монотонно растет. На рис. 17.6, 6 приведен график рабочего ослабления фильтра Чебышева четвертого порядка.
Фильтры Чебышева называют также фильтрами с равноволновой характеристикой ослабления в полосе пропускания.
На рис. 17.7 показаны частотные зависимости квадрата АЧХ фильтра Чебышева для различных значений т, полученные для |Hp(jΩ)|2 из (17.15). Подобные зависимости могут быть построены для рабочего ослабления фильтра.
Чтобы характеристики фильтра отвечали требованиям в полосе непропускання, необходимо выбрать порядок фильтра т. из условия

Сравнивая частотные характеристики фильтров Баттерворта и Чебышева, следует указать, что полиномы Чебышева являются полипомами наилучшего приближения. Это означает, что при одинаковом значении т из всех полиномиальных фильтров, ослабления которых в полосе пропускания не превышают Apmax, наибольшие значения ослабления в полосе непропускання имеет фильтр Чебышева. В частности, рабочее ослабление фильтра Чебышева в полосе испропускания может превышать (п весьма значительно) рабочее ослабление фильтра Баттерворта при равных значениях т и Аpmax. Однако характеристика рабочего ослабления фильтра Баттерворта имеет в полосе пропускания монотонный характер и легче поддается корректированию для устранения искажений передаваемых сигналов.
Выбор типа полиномиальных фильтров определяется конкретными условиями их применения в аппаратуре связи и радиотехнических устройствах.
Для получения передаточной функции фильтра Чебышева поступим аналогично тому, как делали это для фильтров Баттерворта. Заменим оператор jΩ на оператор р и перейдем от функции  к функции:
к функции:
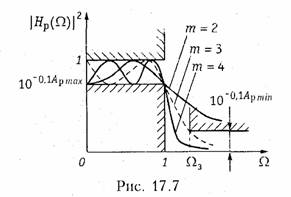



В заключение отметим, что для полиномиальных фильтров в справочниках составлены весьма полные таблицы полюсов и коэффициентов передаточных функций для различных величииApmax и т. Порядок же фильтров т определяется по специальным графикам, исходя из заданных величин Ар max, Apmin и Ω3).
1. http://library.tuit.uz/skanir_knigi/book/osnovi_teorii_cepey/osnov_6.htm
2. http://scask.ru/book_b_toe1.php?id=252 – по 10 вопросу!




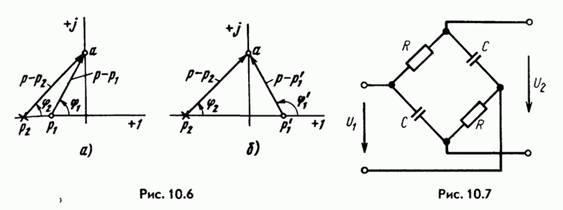






20. Теоре́ма Коте́льникова (в англоязычной литературе — теорема Найквиста — Шеннона или теорема отсчётов) гласит, что, если аналоговый сигнал  имеет финитный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой, строго большей удвоенной верхней частоты
имеет финитный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой, строго большей удвоенной верхней частоты  :
:

Теорема Котельникова
В 1933 году В.А. Котельниковым доказана теорема отсчетов [6, 32], имеющая важное значение в теории связи: непрерывный сигнал 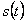 с ограниченным спектром можно точно восстановить (интерполировать) по его отсчетам
с ограниченным спектром можно точно восстановить (интерполировать) по его отсчетам  , взятым через интервалы
, взятым через интервалы  , где
, где  – верхняя частота спектра сигнала.
– верхняя частота спектра сигнала.
В соответствии с этой теоремой сигнал 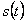 можно представить рядом Котельникова [6, 32]:
можно представить рядом Котельникова [6, 32]:
 . .
| (1.21) |
Таким образом, сигнал 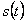 , можно абсолютно точно представить с помощью последовательности отсчетов
, можно абсолютно точно представить с помощью последовательности отсчетов  , заданных в дискретных точках
, заданных в дискретных точках 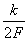 (рис.1.16).
(рис.1.16).

Функции

| (1.22) |
образуют ортогональный базис в пространстве сигналов, характеризующихся ограниченным спектром:
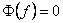 при при  . .
| (1.23) |
Обычно для реальных сигналов можно указать диапазон частот, в пределах которого сосредоточена основная часть его энергии и которым определяется ширина спектра сигнала. В ряде случаев спектр сознательно сокращают. Это обусловлено тем, что аппаратура и линия связи должны иметь минимальную полосу частот. Сокращение спектра выполняют, исходя из допустимых искажений сигнала. Например, при телефонной связи хорошая разборчивость речи и узнаваемость абонента обеспечиваются при передаче сигналов в полосе частот  . Увеличение
. Увеличение  приводит к неоправданному усложнению аппаратуры и повышению затрат. Для передачи телевизионного изображения при стандарте в 625 строк полоса частот, занимаемая сигналом, составляет около 6 МГц.
приводит к неоправданному усложнению аппаратуры и повышению затрат. Для передачи телевизионного изображения при стандарте в 625 строк полоса частот, занимаемая сигналом, составляет около 6 МГц.
Из вышесказанного следует, что процессы с ограниченными спектрами могут служить адекватными математическими моделями многих реальных сигналов.
Функция вида  называется функцией отсчетов (рис.1.17).
называется функцией отсчетов (рис.1.17).
 Она характеризуется следующими свойствами. Если
Она характеризуется следующими свойствами. Если  , функция отсчетов имеет максимальное значение при
, функция отсчетов имеет максимальное значение при 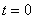 , а в моменты времени
, а в моменты времени  (
(  ) она обращается в нуль; ширина главного лепестка функции отсчетов на нулевом уровне равна
) она обращается в нуль; ширина главного лепестка функции отсчетов на нулевом уровне равна 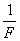 , поэтому минимальная длительность импульса, который может существовать на выходе линейной системы с полосой пропускания
, поэтому минимальная длительность импульса, который может существовать на выходе линейной системы с полосой пропускания  , равна
, равна 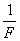 ; функции отсчетов ортогональны на бесконечном интервале времени.
; функции отсчетов ортогональны на бесконечном интервале времени.
На основании теоремы Котельникова может быть предложен следующий способ дискретной передачи непрерывных сигналов:
Для передачи непрерывного сигнала 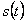 по каналу связи с полосой пропускания
по каналу связи с полосой пропускания  определим мгновенные значения сигнала
определим мгновенные значения сигнала 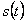 в дискретные моменты времени
в дискретные моменты времени  , (
, (  ). После этого передадим эти значения по каналу связи каким - либо из возможных способов и восстановим на приемной стороне переданные отсчеты. Для преобразования потока импульсных отсчетов в непрерывную функцию пропустим их через идеальный ФНЧ с граничной частотой
). После этого передадим эти значения по каналу связи каким - либо из возможных способов и восстановим на приемной стороне переданные отсчеты. Для преобразования потока импульсных отсчетов в непрерывную функцию пропустим их через идеальный ФНЧ с граничной частотой  .
.
Можно показать, что энергия сигнала находится по формуле [6, 32]:
 . .
| (1.24) |
Для сигнала, ограниченного во времени, выражение (1.24) преобразуется к виду:
 . .
| (1.25) |
Выражение (1.25) широко применяется в теории помехоустойчивого приема сигналов, но является приближенным, т.к. сигналы не могут быть одновременно ограничены по частоте и времени.
Дискретизация и квантование
Дискретизация и квантование исходного сигнала, пропорционального передаваемому сообщению, являются первыми этапами кодирования. Для определения частоты дискретизации (тактовой частоты) используется теорема Котельникова, согласно которой
 ,
,
где  - максимальная частота спектра. Для телефонной передачи достаточно иметь
- максимальная частота спектра. Для телефонной передачи достаточно иметь 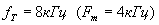 . Для перехода к кодированному импульсному сигналу передается не бесконечное, а конечное число разрешенных значений уровней дискретизированного сигнала, отстоящих друг от друга на конечный интервал. Действительное значение сигнала заменяется ближайшим разрешенным. Шкала разрешенных значений называется шкалой квантования, а интервал между ними – шагом квантования. Квантование по сути является округлением чисел. Естественно, чем меньше шаг квантования, тем ближе квантованные значения к истинным.
. Для перехода к кодированному импульсному сигналу передается не бесконечное, а конечное число разрешенных значений уровней дискретизированного сигнала, отстоящих друг от друга на конечный интервал. Действительное значение сигнала заменяется ближайшим разрешенным. Шкала разрешенных значений называется шкалой квантования, а интервал между ними – шагом квантования. Квантование по сути является округлением чисел. Естественно, чем меньше шаг квантования, тем ближе квантованные значения к истинным.
Пусть исходная функция  подвержена дискретизации и квантованию. Ошибкой кавнтования
подвержена дискретизации и квантованию. Ошибкой кавнтования  называют разность между квантованным значением
называют разность между квантованным значением  и истинным значением
и истинным значением 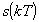 , т.е. передача квантованных значений сигнала вместо истинных равносильна наложению на истинные значения помехи :
, т.е. передача квантованных значений сигнала вместо истинных равносильна наложению на истинные значения помехи :
 .
.
Последовательность  и называют помехой (или шумом) квантования.
и называют помехой (или шумом) квантования.
Квантование позволяет производить дальнейшее кодирование сигнала (например, преобразовывать его в цифровой), и, кроме того, оно представляет собой мощное средство борьбы со случайными помехами, которые всегда возникают в системе связи. На приемном конце мы будем получать сигнал

где  – мгновенное напряжение помехи в момент отсчета. Помеха имеет случайный характер, никак не контролируется, поэтому восстановить истинное значение
– мгновенное напряжение помехи в момент отсчета. Помеха имеет случайный характер, никак не контролируется, поэтому восстановить истинное значение  нельзя.
нельзя.
Если мы знаем  ,то можно применить квантование с шагом, большим
,то можно применить квантование с шагом, большим  . На приемной стороне сигнал
. На приемной стороне сигнал  можно еще раз проквантовать и, таким образом, избавиться от помехи. При округлении ближайшим уровнем окажется тот, который передавался. Таким образом, повторное квантование производит восстановление поврежденного помехой сигнала. Эту операцию можно производить несколько раз, что предотвращает накопление помех. Это используется в радиорелейных линиях связи.
можно еще раз проквантовать и, таким образом, избавиться от помехи. При округлении ближайшим уровнем окажется тот, который передавался. Таким образом, повторное квантование производит восстановление поврежденного помехой сигнала. Эту операцию можно производить несколько раз, что предотвращает накопление помех. Это используется в радиорелейных линиях связи.
Дата добавления: 2018-02-18; просмотров: 1363; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
