Формулы и рисунки к вопросам по курсу «Теория колебаний» (Часть II)
Вопросы по теории колебаний (2-й тест)
1.Вынужденные колебания это
движения на конечном начальном запасе энергии
движения под действием внешнего периодического источника энергии
движение, вызванное изменением энергоемкого параметра за счет внешнего источника
движение, у которого амплитуда, форма и частота зависит только от внутреннего построения системы и не зависит от начальных условий
2.Параметрические колебания это
движения на конечном начальном запасе энергии
движения под действием внешнего периодического источника энергии
движение, вызванное изменением энергоемкого параметра за счет внешнего источника
движение, у которого амплитуда, форма и частота зависит только от внутреннего построения системы и не зависит от начальных условий
3.Автоколебания это
движения на конечном начальном запасе энергии
движения под действием внешнего периодического источника энергии
движение, вызванное изменением энергоемкого параметра за счет внешнего источника
движение у которого амплитуда, форма и частота зависит только от внутреннего построения системы и не зависит от начальных условий
4. Постоянная времени это
временной интервал в течение которого амплитуда уменьшается в е—раз
величина обратная добротности
временной интервал в течение которого амплитуда уменьшается до 0
5. Логарифмически декремент затухания определяется как
|
|
|
натуральный логарифм отношения текущей амплитуды к амплитуде через условный период
логарифм от величины обратной добротности
временной интервал в течение которого амплитуда уменьшается до 0
6. Коэффициент затухания это
натуральный логарифм отношения текущей амплитуды к амплитуде через условный период
величина обратная добротности
временной интервал в течение, которого амплитуда уменьшается до 0
величина обратная постоянной времени
7. Особая точка это
точка, через которую проходит несколько интегральных кривых
точка, через которую проходит только одна интегральная кривая
точка пересечения координат
8. Логарифмический декремент затухания (см. рисунок 1) можно рассчитать по следующей формуле
Формула 1
Формула 2
Формула 3
9. Система уравнений (4) описывает
нелинейную систему
систему с кулоновским трением
линейную систему
параметрическую систему
10. Состояние равновесия устойчиво по Ляпунову
если система совершает колебания вблизи состояния
если система с течением времени возвращается в состояние равновесия
если система удаляется от состояния равновесия
11. Состояние равновесия абсолютно устойчиво
|
|
|
если система совершает колебания вблизи состояния
если система с течением времени возвращается в состояние равновесия
если система удаляется от состояния равновесия
12. Оцените устойчивость системы, если корни характеристического уравнения имеют вид (см. формулу 5) и выполняются условия (6)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунова
13. Оцените устойчивость системы если корни характеристического уравнения имеют вид (см. формулу 5) и выполняются условия (7)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунова
14. Система уравнений (8) описывает
нелинейную систему N-го порядка
систему с кулоновским трением
линейную систему N-го порядка
параметрическую систему
15. Система первого приближения получается из системы уравнений (9) после отброса
производных первого порядка в правой части
приравнивания левых частей уравнений к нулю
нелинейных членов второго порядка малости
нелинейных членов, чей порядок не превышает второго порядка малости
16. Если все корни характеристического уравнения системы первого приближения имеют отрицательные вещественные части, то соответствующее состояние равновесия нелинейной системы
|
|
|
асимптотически устойчиво
устойчиво по Ляпунову
неустойчиво
невозможно сделать заключение об устойчивости или неустойчивости исходной системы
17. Если среди корней характеристического уравнения системы первого приближения встречается хотя бы один корень с положительной вещественной частью, то соответствующее состояние равновесия нелинейной системы
асимптотически устойчиво
устойчиво по Ляпунову
неустойчиво
невозможно сделать заключение об устойчивости или неустойчивости исходной системы
18. Если среди корней характеристического уравнения системы первого приближения встречается хотя бы один корень с нулевой вещественной частью, то соответствующее состояние равновесия нелинейной системы
асимптотически устойчиво
устойчиво по Ляпунову
неустойчиво
невозможно сделать заключение об устойчивости или неустойчивости исходной системы
19.Уравнение (10) описывает
колебания в линейной системе при внешнем воздействии
колебания в нелинейной системе при внешнем воздействии
свободные колебания в линейной системе
свободные колебания в нелинейной системе
|
|
|
20.Уравнение (11) описывает
колебания в линейной системе при внешнем воздействии
колебания в нелинейной системе при внешнем воздействии
свободные колебания в линейной системе
свободные колебания в нелинейной системе
21.Уравнение (12) описывает
общее решение неоднородного дифференциального уравнения
колебания в нелинейной системе при внешнем воздействии
свободные колебания в линейной системе
свободные колебания в нелинейной системе
22.Первый член уравнения (13) соответствует
частному решению уравнения (10)
частному решению уравнения (11)
решению уравнения (10) при 
решению уравнения (11) при 
23.Второй член уравнения (13) соответствует
частному решению уравнения (10)
частному решению уравнения (11)
решению уравнения (10) при 
решению уравнения (11) при 
24.Общим решением неоднородного дифференциального уравнения является
Первый член уравнения (13)
Второй член уравнения (13)
Уравнения (13)
25.Принцип суперпозиции применим для рассмотрения
вынужденных колебаний в линейных системах
вынужденных колебаний в нелинейных системах
параметрических колебаний
свободных колебаний в нелинейных системах
26. Решение уравнения (14) может быть найдено методом
комплексных амплитуд
вариации постоянной Лапласа
медленно меняющихся амплитуд
27. Уравнение (15) описывает
вынужденные колебания в линейной системе при гармоническом воздействии
вынужденные колебания в линейной системе при произвольном воздействии
вынужденные колебания в нелинейной системе при произвольном воздействии
вынужденные колебания в нелинейной системе при гармоническом воздействии
28. Метод комплексных амплитуд применим для анализа
вынужденные колебания в линейной системе при гармоническом воздействии
вынужденные колебания в линейной системе при произвольном воздействии
вынужденные колебания в нелинейной системе при произвольном воздействии
вынужденные колебания в нелинейной системе при гармоническом воздействии
29. Суть метода комплексных амплитуд заключается в том, что решение уравнения (14) сводится
к решению уравнения (16)
к решению уравнения (17)
к решению уравнения (18)
30. Комплексная амплитуда вынужденных колебаний в линейной системе описывается
формулой 19
формулой 20
формулой 21
31. Амплитудно─частотная характеристика линейной системы описывается
формулой 19
формулой 20
формулой 21
32. Фазо─частотная характеристика линейной системы описывается
формулой 19
формулой 20
формулой 21
33. Амплитуда вынужденных колебаний в линейной системе определяется
формулой 19
формулой 20
формулой 21
34. Амплитуда вынужденных колебаний в линейной системе определяется
формулой 19
формулой 20
формулой 21
35. При воздействии на линейную систему внешней гармонической силы с частотой  в системе возбуждаются колебания
в системе возбуждаются колебания
с частотой 
с частотой 
с частотой 
с частотой 
36. Резонансом называется
явление резкого увеличения амплитуды вынужденных колебаний на некоторой частоте
явление линейного роста амплитуды в системе с отрицательным сопротивлением
явление взаимодействия собственных колебаний системы с колебаниями внешнего источника
37. Биениями в колебательной системе называется
явление резкого увеличения амплитуды вынужденных колебаний на некоторой частоте
явление линейного роста амплитуды в системе с отрицательным сопротивлением
явление взаимодействия собственных колебаний системы с колебаниями внешнего источника
38. Уравнение (22) описывает вынужденные колебания
в линейной системе при включении источника гармонических колебаний
в нелинейной системе при включении источника гармонических колебаний
в линейной системе при произвольном воздействии
в нелинейной системе при произвольном воздействии
39. В формуле (22), 1 и 2 члены уравнения описывают
общее решение неоднородного дифференциального уравнения
частное решение неоднородного дифференциального уравнения
решение однородного дифференциального уравнения
40. В формуле (22), 3 член уравнения описывает
общее решение неоднородного дифференциального уравнения
частное решение неоднородного дифференциального уравнения
решение однородного дифференциального уравнения
41. Колебания в системе описанной формулой (22) имеют вид
рисунок 2
рисунок 3
рисунок 4
42. При воздействии на линейную систему источника гармонических колебаний с частотой  вынужденные колебания имеют вид
вынужденные колебания имеют вид
рисунок 2
рисунок 3
рисунок 4
43. При воздействии на линейную систему источника гармонических колебаний с частотой  вынужденные колебания имеют вид
вынужденные колебания имеют вид
рисунок 2
рисунок 3
рисунок 4
44. Частота высокочастотного колебания сигнала биений (рисунок 3) равна




45. Частота вынужденных колебания (рисунок 3), на линейную систему, при воздействии внешнего источника с частотой  (рисунок 2) равна
(рисунок 2) равна




46. Гармонический осциллятор при произвольном внешнем воздействии может быть описан дифференциальным уравнением вида
формула 10
формула 14
формула 22
формула 23
47. Частное решение для гармонического осциллятора ищется в виде
@формула 17
формула 18
формула 22
48. Метод вариации постоянной Лагранжа основан на том, что решение ищется в виде
гармонического колебания с частотой внешнего воздействия
гармонического колебания с резонансной частотой
гармонического колебания с частотой 
гармонического колебания с частотой 
49. Уравнение связи функции  с функциями
с функциями 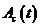 и
и 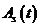 в формуле (17) может быть получено из формулы (24) путем
в формуле (17) может быть получено из формулы (24) путем
исключения 1 и 2 члена уравнения (24)
исключения 3 и 4 члена уравнения (24)
приравнивания к нулю 1 и 2 члена уравнения (24)
приравнивания к нулю 3 и 4 члена уравнения (24)
50. Уравнение связи функции  с функциями
с функциями 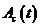 и
и 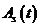 (условие Лагранжа) имеет вид
(условие Лагранжа) имеет вид
формула 24
уравнение 1 в системе (25)
уравнение 2 в системе (25)
51. Производные  и
и  могут быть найдены из системы (25) путем
могут быть найдены из системы (25) путем
решения системы алгебраических уравнений относительно  и
и 
прямого интегрирования уравнений системы (25)
интегрирования методом разделения переменных
подстановки в систему (25) начальных условий
52. Уравнение (26) может быть записано в виде (27) если функция  является
является
линейной
четной
нечетной
тригонометрической
53. Уравнением Дуффинга является
уравнение (26)
уравнение (27)
уравнение (28)
54. Уравнение (27) описывает колебательный процесс в
колебательном контуре
математическом маятнике
автогенераторе
пружинном маятнике
55. Задача Дуффинга может быть решена
методом Эйлера
методом медленно меняющихся амплитуд
методом гармонического баланса
методом вариации постоянной Лагранжа
56. Для анализа автоколебательных систем пользуются
методом Эйлера
методом медленно меняющихся амплитуд
методом гармонического баланса
методом вариации постоянной Лагранжа
57. Используя формулу (29) определите к какому типу относится колебательная система
с «жесткой» характеристикой упругой силы
с «мягкой» характеристикой упругой силы
с линейной характеристикой упругой силы
58. Используя рисунок (7) определите к какому типу относится колебательная система
с «жесткой» характеристикой упругой силы
с «мягкой» характеристикой упругой силы
с линейной характеристикой упругой силы
59. Используя рисунок (5) определите к какому типу относится колебательная система
с «жесткой» характеристикой упругой силы
с «мягкой» характеристикой упругой силы
с линейной характеристикой упругой силы
60. Используя рисунок (6) определите к какому типу относится колебательная система
с «жесткой» характеристикой упругой силы
с «мягкой» характеристикой упругой силы
с линейной характеристикой упругой силы
61. Используя рисунок (5) определите значение коэффициента  в уравнении (27)
в уравнении (27)



62. Используя рисунок (5) определите значение коэффициента  в уравнении (27)
в уравнении (27)



63. Метод гармонического баланса применим для
нелинейных систем при 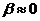
линейных систем при 
нелинейных систем при 
64. При использовании метода гармонического баланса решение уравнения (27) ищется в виде
формула (17)
формула (18)
формула (30)
65. Метод гармонического баланса применим для нелинейных систем при
гармоническом воздействии
произвольном воздействии
только при гармоническом воздействии на резонансной частоте
66. При анализе системы методом гармонического баланса
отыскивается установившееся колебание
анализируется переходной процесс
отыскиваются временные характеристики переходного процесса
67. В уравнении (31) укажите слагаемое от которое определяет точность решения
1─е слагаемое
2─е слагаемое
3─е слагаемое
68. В уравнении (31) укажите какие из слагаемых необходимо приравнять к нулю чтобы найти (А,Ф)
1 и 2
1 и 3
2 и 3
1
69. Пользуясь рисунком (8) укажите частоты на которых существует неоднозначность амплитуд



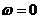
70. Пользуясь рисунком (8) укажите частоты на которых происходят скачки фаз



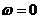
71. Какая из отмеченных на рисунке 10 областей является рабочей для феррорезонансных стабилизаторах напряжения.
Область 1
Область 2
Область 3
Область 4
72. Какая из отмеченных на рисунке 11 областей является рабочей для генератора на туннельном диоде
Область А
Область Б
Область В
73. Какая из отмеченных областей (рисунок 11) является участком с отрицательным сопротивлением.
Область Б
Область А
Область В
74. Пользуясь рисунком 11 укажите на вольт─амперной характеристике рабочую точку туннельного диода
1
2
3
4
75. Укажите условие самовозбуждения лампового генератора
формула 36
формула 37
формула 38
формула 40
76. Укажите условие при котором самовозбуждение лампового генератора невозможно
формула 36
формула 37
формула 38
формула 40
77. Укажите условие при котором на выходе лампового генератора установятся автоколебания с постоянной амплитудой
формула 36
формула 37
формула 38
формула 40
78. Укажите условие самовозбуждения автогенератора на туннельном диоде
формула 39
формула 40
формула 41
формула 38
79. Укажите условие при котором самовозбуждение автогенератора на туннельном диоде невозможно
формула 38
формула 39
формула 41
формула 40
80. Укажите условие при котором на выходе автогенератора на туннельном диоде установятся автоколебания с постоянной амплитудой
формула 39
формула 41
формула 38
формула 40
Формулы и рисунки к вопросам по курсу «Теория колебаний» (Часть II)
1. 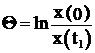 2.
2.  3.
3.  4.
4. 
5.  6.
6.  ,
,  7.
7.  ,
, 
8. 
9.  10.
10.  11.
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 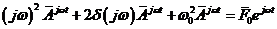
17.  18.
18. 
19.  20.
20.  21.
21. 
22. 
 23.
23. 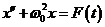
24. 
25. 
26.  27.
27.  28.
28. 
29.  30.
30. 
31. 
32.  33.
33.  34.
34.  35.
35. 
36.  37.
37.  38.
38. 
39.  40.
40.  41.
41. 

Дата добавления: 2018-02-18; просмотров: 981; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
