Формулы и рисунки к вопросам по курсу «Теория колебаний» (Часть I)
Nbsp;
Вопросы по теории колебаний (Часть I)
1. Колебанием называется
изменение амплитуды от минимального до максимального значения
периодически повторяющееся движение системы около некоторого состояния
непрерывное движение системы
2. Колебания согласно теории колебаний классифицируются по
физическим признакам
кинематическим признакам
частотным признакам
3. Число степеней свободы
равно числу независимых координат которые полностью описывают движение системы
равно порядку дифференциального уравнения
равно числу колебательных движений в течение времени релаксации
4. Консервативная система это
система, в которой потери компенсируются за счет внешнего источника
система, в которой потери отсутствуют
система, в которой потери компенсируются за счет отрицательного сопротивления
5. Диссипативная система это
система, в которой происходит изменение энергоемкого параметра за счет внешнего источника
система, в которой потери отсутствуют
система, в которой присутствуют потери энергии или поступление энергии со стороны внешнего источника
6.Собственные колебания это
движения на конечном начальном запасе энергии
движения под действием внешнего периодического источника энергии
движение, вызванное изменением энергоемкого параметра за счет внешнего источника
движение, у которого амплитуда, форма и частота зависит только от внутреннего построения системы и не зависит от начальных условий
|
|
|
7.Вынужденные колебания это
движения на конечном начальном запасе энергии
движения под действием внешнего периодического источника энергии
движение, вызванное изменением энергоемкого параметра за счет внешнего источника
движение, у которого амплитуда, форма и частота зависит только от внутреннего построения системы и не зависит от начальных условий
8.Параметрические колебания это
движения на конечном начальном запасе энергии
движения под действием внешнего периодического источника энергии
движение, вызванное изменением энергоемкого параметра за счет внешнего источника
движение, у которого амплитуда, форма и частота зависит только от внутреннего построения системы и не зависит от начальных условий
9.Автоколебания это
движения на конечном начальном запасе энергии
движения под действием внешнего периодического источника энергии
движение, вызванное изменением энергоемкого параметра за счет внешнего источника
движение у которого амплитуда, форма и частота зависит только от внутреннего построения системы и не зависит от начальных условий
|
|
|
10. Уравнение (1) описывает
собственные колебания в системе без потерь
собственные колебания в системе с потерями
вынужденные колебания
11. Уравнение (2) описывает
собственные колебания в системе без потерь
собственные колебания в системе с потерями
вынужденные колебания
12. Уравнение (3) описывает
собственные колебания в системе без потерь
собственные колебания в линейной системе с потерями
вынужденные колебания
собственные колебания в нелинейной системе с потерями
13. Уравнение (4) описывает
собственные колебания в системе без потерь
собственные колебания в линейной системе с потерями
вынужденные колебания
собственные колебания в нелинейной системе с потерями
14. Постоянная времени это
временной интервал в течение которого амплитуда уменьшается в е—раз
величина обратная добротности
временной интервал в течение которого амплитуда уменьшается до 0
15. Логарифмически декремент затухания определяется как
натуральный логарифм отношения текущей амплитуды к амплитуде через условный период
логарифм от величины обратной добротности
временной интервал в течение которого амплитуда уменьшается до 0
|
|
|
16. Коэффициент затухания это
натуральный логарифм отношения текущей амплитуды к амплитуде через условный период
величина обратная добротности
временной интервал в течение, которого амплитуда уменьшается до 0
величина обратная постоянной времени
17. Метод фазовой плоскости используется
для анализа вынужденных колебаний
для анализа систем с двумя и более степенями свободы
для анализа систем с одной степенью свободы
18. Особая точка это
точка, через которую проходит несколько интегральных кривых
точка, через которую проходит только одна интегральная кривая
точка пересечения координат
19. Особая точка типа центр это
изолированная особая точка, окруженная замкнутыми траекториями вложенных друг в друга.
изолированная особая точка являющаяся асимптотической для интегральных кривых типа спираль, вложенных друг в друга.
изолированная особая точка через которую проходят интегральные кривые типа парабол.
изолированная особая точка через которую проходят две интегральные кривые, являющиеся асимптотами для кривых типа гипербол.
20. Особая точка типа фокус это
изолированная особая точка, окруженная замкнутыми траекториями вложенных друг в друга.
|
|
|
изолированная особая точка являющаяся асимптотической для интегральных кривых типа спираль, вложенных друг в друга.
изолированная особая точка, через которую проходят интегральные кривые типа парабол.
изолированная особая точка, через которую проходят две интегральные кривые, являющиеся асимптотами для кривых типа гипербол.
21. Особая точка типа узел это
изолированная особая точка, окруженная замкнутыми траекториями вложенных друг в друга.
изолированная особая точка являющаяся асимптотической для интегральных кривых типа спираль, вложенных друг в друга.
изолированная особая точка через которую проходят интегральные кривые типа парабол.
изолированная особая точка через которую проходят две интегральные кривые, являющиеся асимптотами для кривых типа гипербол.
22. Особая точка типа седло это
изолированная особая точка, окруженная замкнутыми траекториями, вложенных друг в друга.
изолированная особая точка являющаяся асимптотической для интегральных кривых типа спираль, вложенных друг в друга.
изолированная особая точка, через которую проходят интегральные кривые типа парабол.
изолированная особая точка, через которую проходят две интегральные кривые, являющиеся асимптотами для кривых типа гипербол.
23. Особая точка типа центр показывает, что
колебания периодические
колебания затухают во времени
система не устойчива
система устойчива
24. Особая точка типа фокус показывает, что
колебания периодические
колебания затухают во времени
система не устойчива
система устойчива
25. Особая точка типа узел показывает, что
колебания периодические
амплитуда колебания затухают во времени
система не устойчива
система устойчива
26. Особая точка типа седло показывает, что
колебания периодические
колебания затухают во времени
система не устойчива
система устойчива
27. Фазовый портрет позволяет получить
информацию о типе колебаний
информацию о периоде колебаний
временную диаграмму колебательного процесса
28. По какому из приведенных фазовых портретов можно определить логарифмический декремент затухания
особая точка типа «центр»
особая точка типа «фокус»
особая точка типа «седло»
29. Уравнение (5) описывает систему, имеющую на фазовом портрете особую точку типа
«центр»
«фокус»
«седло»
«узел»
30. Уравнение (6) описывает систему, имеющую на фазовом портрете особую точку типа
«центр»
«фокус»
«седло»
«узел»
31. Уравнение (7) описывает систему, имеющую на фазовом портрете особую точку типа
«центр»
«фокус»
«седло»
«узел»
32. Уравнение (8) описывает систему, имеющую на фазовом портрете особую точку типа
«центр»
«фокус»
«седло»
«узел»
33. Уравнение (9) описывает систему, имеющую на фазовом портрете особую точку типа
«центр»
«фокус»
«седло»
«узел»
34. Изоклиной называется
интегральная кривая, полученная при решение уравнения приближенным графическим способом
геометрическое место точек, в которых угол наклона касательных к интегральным кривым постоянен
интегральная кривая, полученная при решение уравнения аналитическим способом
35. Сепаратриса это
геометрическое место точек в которых угол наклона касательных к интегральным кривым постоянен
фазовая траектория, которая разделяет фазовую плоскость на области с разными типами движения
постоянная величина характеризующая затухание в динамической системе
36. При построении фазового портрета графическим способом исходным является
график изменения потенциальной энергии
график изменения кинетической энергии
график изменения энергии поступающей от внешнего источника
37. Указать значение логарифмического декремента затухания, если добротность системы с потерями равна 100
0.0314
0.0522
0.0724
0.025
38. Указать значение коэффициента затухания, если условный период равен 0.1 сек., а логарифмический коэффициент затухания равен 0.06
0.1
0.2
0.4
0.6
39. . Указать значение постоянной времени, если условный период равен 0.1 сек., а логарифмический коэффициент затухания равен 0.05
0.25 сек
0.5 сек
1.0 сек
2.0 сек
40. Укажите, какой временной интервал является постоянной времени (Рисунок 1)
T1
T2
Т3
41. Укажите, какой временной интервал является условным периодом (Рисунок 1)
T1
T2
Т3
42. Логарифмический декремент затухания (см. рисунок 1) можно рассчитать по следующей формуле
Формула 10
Формула 11
Формула 12
42. Логарифмический декремент затухания (см. рисунок 2) можно рассчитать по следующей формуле
Формула 13
Формула 14
Формула 15
43. Какие из предложенных формул относятся к исследованию систем методом фазовой плоскости с непосредственным интегрированием
16, 19, 21.
16, 19, 20.
16,17, 18.
44. Какие из предложенных формул относятся к исследованию систем методом Эйлера
16, 19, 21.
16, 19, 20.
16,17, 18.
45. Какие из предложенных формул относятся к исследованию систем методом фазовой плоскости с использованием метода изоклин
16, 19, 21.
16, 19, 20.
16,17, 18.
46. Транзисторный генератор будет иметь особую точку типа неустойчивый фокус, если будут реализованы следующие условия (см. формулу 22)
Формула 23
Формула 24
Формула 25
47. Транзисторный генератор будет иметь особую точку типа устойчивый фокус, если будут реализованы следующие условия (см. формулу 22)
Формула 23
Формула 24
Формула 25
48. Транзисторный генератор будет иметь особую точку типа центр если будут реализованы следующие условия (см. формулу 22)
Формула 23
Формула 24
Формула 25
49. Пользуясь рисунком 3 указать временную характеристику движения системы для начальных условий, попадающих в зону 1а─1б
Рисунок 4
Рисунок 5
Рисунок 6
50. Пользуясь рисунком 3 указать временную характеристику движения системы для начальных условий, попадающих в зону 2а─2б
Рисунок 4
Рисунок 5
Рисунок 6
51. Пользуясь рисунком 3 указать временную характеристику движения системы для начальных условий, попадающих в зону 3а─3б
Рисунок 4
Рисунок 5
Рисунок 6
52. Фазовый портрет (рисунок 7) позволяет сделать заключение, что система описывается уравнением вида
Формула 26
Формула 27
Формула 28
Формула 29
53. Фазовый портрет (рисунок 8) позволяет сделать заключение, что система описывается уравнением вида
Формула 26
Формула 27
Формула 28
Формула 29
54. Фазовый портрет (рисунок 9) позволяет сделать заключение, что система описывается уравнением вида
Формула 26
Формула 27
Формула 28
Формула 29
55. Фазовый портрет (рисунок 10) позволяет сделать заключение, что система описывается уравнением вида
Формула 26
Формула 27
Формула 28
Формула 29
56. Для построения фазового портрета графическим способом необходимо использовать следующую формулу
Формула 30
Формула 31
Формула 20
57. На рисунке 11 указать сепаратису
Кривая 1
Кривая 2
Кривая 3
Кривая 4
58. На рисунке 11 указать график изменения потенциальной энергии
Кривая 1
Кривая 2
Кривая 3
Кривая 4
59. На рисунке 11 указать фазовую траекторию соответствующую вращательному движению
Кривая 1
Кривая 2
Кривая 3
Кривая 4
60. На рисунке 11 указать фазовую траекторию соответствующую колебательному процессу с ограниченной амплитудой
Кривая 1
Кривая 2
Кривая 3
Кривая 4
61. Какое из приведенных уравнений описывает процесс изображенный на рис.12
Формула 26
Формула 27
Формула 28
Формула 29
62. Какая из приведенных на рис. 11 фазовых траекторий будет соответствовать квазигармоническому колебанию
Кривая 1
Кривая 2
Кривая 3
Кривая 4
63. Метод поэтапного рассмотрения заключается в том, что
движение системы разбивают на этапы каждый из которых описывается известным уравнением
уравнение второго порядка представляют в виде двух уравнений первого порядка
нелинейные функции представляют в виде суммы линейных функций
64. Какое из приведенных уравнений описывает процессы в системе с кулоновским трением
Формула 26
Формула 28
Формула 30
Формула 32
65. Укажите форму фазового портрета для системы изображенной на рис.13
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
66. Укажите форму фазового портрета для системы изображенной на рис.14
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
67. Укажите форму фазового портрета для системы изображенной на рис.15
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
68. Укажите форму фазового портрета для системы изображенной на рис.16
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
69. Укажите форму фазового портрета для системы изображенной на рис.17
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
70. Укажите формулу, которая описывает процессы в системе с потерями при условии, что зависимость силы трения от координаты имеет вид (см. рис.15)
Формула 26
Формула 28
Формула 30
Формула 32
71. Фазовый портрет приведенный на рисунке 11 соответствует системе
Нелинейной системе с малым затуханием
Линейной системе с малым затуханием
Нелинейной системе с большим затуханием
Линейной системе с большим затуханием
72. Если физический маятник находится в воздушной среде, то каким из приведенных уравнений он может быть описан
Формула 26
Формула 28
Формула 30
Формула 32
73. Если физический маятник находится в водной среде, то каким из приведенных уравнений он может быть описан
Формула 26
Формула 28
Формула 27
Формула 32
74. Какой из приведенных ниже фазовых портретов адекватно отражает поведение маятника в воздушной среде (см.рис 18)
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
75. Какой из приведенных ниже фазовых портретов адекватно отражает поведение маятника в водной среде (см.рис 18)
Рисунок 7
Рисунок 3
Рисунок 9
Рисунок 10
76. Какой из приведенных ниже фазовых портретов адекватно отражает поведение маятника в воздушной среде (см.рис 19)
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
77. Какой из приведенных ниже фазовых портретов адекватно отражает поведение маятника в водной среде (см.рис 19) при условии, что маятник тяжелее воды
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
78. Укажите точки сшивания решений если динамическое уравнение системы имеет вид (32)
А
Б
В
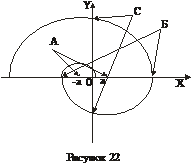
79. На рисунке 22 укажите точки сшивания решений на фазовом портрете если динамическое уравнение системы имеет вид (32)
А
Б
В
80. Для схемы изображенной на рисунке 20 укажите фазовый портрет адекватно отражающий колебательный процесс (см. рис.21)
А
Б
В
81. Система уравнений (32) описывает
нелинейную систему
систему с кулоновским трением
линейную систему
параметрическую систему
82. Состояние равновесия устойчиво по Ляпунову
если система находится вблизи состояния
если система с течением времени возвращается в состояние равновесия
если система удаляется от состояния равновесия
83. Состояние равновесия абсолютно устойчиво
если система находится вблизи состояния
если система с течением времени возвращается в состояние равновесия
если система удаляется от состояния равновесия
84. Оцените устойчивость системы, если корни характеристического уравнения имеют вид (см. формулу 33) и выполняются условия (34)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунова
85. Оцените устойчивость системы если корни характеристического уравнения имеют вид (см. формулу 33) и выполняются условия (35)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунова
86. Оцените устойчивость системы если корни характеристического уравнения имеют вид (см. формулу 33) и выполняются условия (36)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунова
87. Оцените устойчивость системы если корни характеристического уравнения имеют вид (см. формулу 33) и выполняются условия (37)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунова
88. Система считается «грубой»
если тип движения резко меняется при малом изменении параметра системы
если тип движения слабо зависит от малого изменения параметра системы
если в системе присутствуют потери
если в системе присутствует вклад энергии
89. Система считается «не грубой»
если тип движения резко меняется при малом изменении параметра системы
если тип движения слабо зависит от малого изменения параметра системы
если в системе присутствуют потери
если в системе присутствует вклад энергии
90. Под термином «бифуркация» понимают
изменение характера движения в колебательной системе
резкое изменение амплитуды движения
смещение резонансной частоты системы
91. Система уравнений (38) описывает
нелинейную систему N-го порядка
систему с кулоновским трением
линейную систему N-го порядка
параметрическую систему
92. Критерий Рауса─Гурвица предназначен для оценки
возможности решения системы (38)
устойчивости системы
предельных параметров колебаний
типа колебаний в системе
93. Решите вопрос об устойчивости системы, если в ходе решения получилось уравнение вида (39) и матрица Гурвицы имеет вид (40)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунову
94. Решите вопрос об устойчивости системы, если в ходе решения получилось уравнение вида (39) и матрица Гурвицы имеет вид (41)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунову
95. Решите вопрос об устойчивости системы, если в ходе решения получилось уравнение вида (39) и матрица Гурвицы имеет вид (42)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунову
96. Решите вопрос об устойчивости системы, если в ходе решения получилось уравнение вида (39) и матрица Гурвицы имеет вид (43)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунову
97. Решите вопрос об устойчивости системы если в ходе решения получилось уравнение вида (39) и матрица Гурвицы имеет вид (44)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунову
98. Решите вопрос об устойчивости системы, если в ходе решения получилось уравнение вида (39) и матрица Гурвицы имеет вид (45)
система неустойчива
система абсолютно устойчива
система устойчива по Ляпунову
99. Система уравнений (46) описывает
нелинейную систему N-го порядка
систему с кулоновским трением
линейную систему N-го порядка
параметрическую систему
100. Система первого приближения получается из системы уравнений (47) после отброса
производных первого порядка в правой части
приравнивания левых частей уравнений к нулю
нелинейных членов второго порядка малости
нелинейных членов, чей порядок не превышает второго порядка малости
101. Если все корни характеристического уравнения системы первого приближения имеют отрицательные вещественные части, то соответствующее состояние равновесия нелинейной системы
асимптотически устойчиво
устойчиво по Ляпунову
неустойчиво
невозможно сделать заключение об устойчивости или неустойчивости исходной системы
102. Если среди корней характеристического уравнения системы первого приближения встречается хотя бы один корень с положительной вещественной частью, то соответствующее состояние равновесия нелинейной системы
асимптотически устойчиво
устойчиво по Ляпунову
неустойчиво
невозможно сделать заключение об устойчивости или неустойчивости исходной системы
103. Если среди корней характеристического уравнения системы первого приближения встречается хотя бы один корень с нулевой вещественной частью, то соответствующее состояние равновесия нелинейной системы
асимптотически устойчиво
устойчиво по Ляпунову
неустойчиво
невозможно сделать заключение об устойчивости или неустойчивости исходной системы
Формулы и рисунки к вопросам по курсу «Теория колебаний» (Часть I)
1. 
2. 
3. 
4. 
5.  ,
, 
6.  ,
, 
7.  ,
, 
8.  ,
, 
9. 
10.  11.
11.  12.
12.  13.
13.  14.
14. 
15. 
16. 
17. 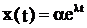
18. 
19.  20.
20.  21.
21. 
22. 
23. 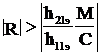 ; при
; при 
24.  ; при
; при 
25.  ; при
; при 
26. 
27. 

28. 

29. 

30. 
31. 
32. 
33. 
34.  ,
, 
35.  ,
, 
36.  ,
,  ,
, 
37.  ,
,  ,
, 
38. 
39. 
40.  41.
41.  42.
42. 
43.  44.
44. 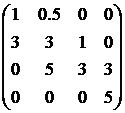 45.
45. 
46. 
47. 


Дата добавления: 2018-02-18; просмотров: 725; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
