Вопросы к коллоквиуму по математическому анализу (1 семестр)
Конспект лекций для подготовки к коллоквиуму (МП-16,17,17а,18,19)
Элементы математической логики.
Основное понятие – высказывание. Высказывание – предложение, сформулированное средствами некоторого языка, относительно которого можно сказать истинно оно или ложно.
1) девять делится на три без остатка;
2) 5>4;
3) 8 – простое число;
4)  ;
;
5) Да здравствует математика!
Высказываниями являются три первых предложения. Пятое предложение не является высказыванием. Четвертое предложение – предикат. Предикат – предложение, содержащее переменную величину, переходящее в высказывание при конкретном значении этой величины. Например, припишем слева к  «квантор» всеобщности
«квантор» всеобщности  («для любого», «для каждого», «для всех» ) или квантор существования
(«для любого», «для каждого», «для всех» ) или квантор существования  ( «найдется», «существует» ).
( «найдется», «существует» ).
 - ложь.
- ложь.
 - истина.
- истина.
Знак истинности у ложного высказывания «0», знак истинности у истинного высказывания «1».
Над высказываниями можно проводить логические операции, результатом которых является новое высказывание. Результаты операций представлены в таблице истинности:
| A | B | А «и» В

| А «или» В

| «Не» А

| Из А «следует» В

| А «тождественно» В

|
| 0 0 1 1 | 0 1 0 1 | 0 0 0 1 | 0 1 1 1 | 1 1 0 0 | 1 1 0 1 | 1 0 0 1 |
Два высказывания, имеющие одинаковые переменные, называются тождественными, если их таблицы истинности совпадают.
|
|
|
1. 
2. 
3. 
4. 
5. 
6. 
Множества.
Множество – совокупность некоторых объектов определенной природы. Объекты, образующие множество, называются его элементами.
 - элемент
- элемент  принадлежит множеству
принадлежит множеству  .
.
 - элемент
- элемент  не принадлежит множеству
не принадлежит множеству  .
.
Задать множество можно перечислением его элементов  ; с помощью некоторой процедуры
; с помощью некоторой процедуры  ; при помощи описания свойств элементов, входящих в множество,
; при помощи описания свойств элементов, входящих в множество,  .
.
 - множество
- множество  является подмножеством
является подмножеством  , т. е. каждый элемент множества
, т. е. каждый элемент множества  является элементом множества
является элементом множества  .
.
 - пустое множество. Множество, состоящее из
- пустое множество. Множество, состоящее из  элементов, содержит с учетом пустого подмножества
элементов, содержит с учетом пустого подмножества  подмножеств.
подмножеств.
 - равные множества.
- равные множества.
 - множество, элементы которого являются элементами множества
- множество, элементы которого являются элементами множества  или множества
или множества  или элементами обоих множеств (объединение множеств).
или элементами обоих множеств (объединение множеств).
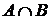 - множество, элементы которого являются элементами множества
- множество, элементы которого являются элементами множества  и одновременно элементами множества
и одновременно элементами множества  (пересечение множеств).
(пересечение множеств).
 - множество, элементы которого являются элементами множества
- множество, элементы которого являются элементами множества  , не принадлежащие множеству
, не принадлежащие множеству  (разность множеств).
(разность множеств).
Множества  и
и  называются эквивалентными, если между элементами множеств можно установить взаимно однозначное соответствие. Конечные множества эквивалентны тогда и только тогда, когда они содержат одинаковое количество элементов.
называются эквивалентными, если между элементами множеств можно установить взаимно однозначное соответствие. Конечные множества эквивалентны тогда и только тогда, когда они содержат одинаковое количество элементов.
|
|
|
В случае бесконечного множества эквивалентными могут быть все множество и его подмножество. Например, с помощью процедуры  мы можем установить взаимно однозначное соответствие между множеством натуральных чисел и множеством четных натуральных чисел, т. е. установить их эквивалентность.
мы можем установить взаимно однозначное соответствие между множеством натуральных чисел и множеством четных натуральных чисел, т. е. установить их эквивалентность.
Счетное множество – множество, эквивалентное множеству натуральных чисел. Можно показать, что счетным множеством является множество рациональных чисел. Множество иррациональных чисел не является счетным.
Множество действительных чисел.
Понятия действительных чисел, их свойства формулировались в течение длительного времени. Аксиоматический подход к понятию действительных чисел заключается в том, что действительными числами называют множество, элементы которого обладают следующими свойствами (удовлетворяют следующим аксиомам).
I.Аксиомы сложения.
1.  - переместительный.
- переместительный.
2.  - сочетательный.
- сочетательный.
3. 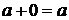 - существует «0».
- существует «0».
4.  - существует противоположное число.
- существует противоположное число.
II. Аксиомы умножения.
1.  - - переместительный.
- - переместительный.
|
|
|
2.  - сочетательный.
- сочетательный.
3.  - существует «1».
- существует «1».
4. 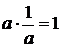 - существует обратное число.
- существует обратное число.
5.  - распределительный.
- распределительный.
III. Аксиомы порядка.
1. Если  , то
, то  или
или  .
.
2. Если  и
и  , то
, то  .
.
3. Если  , то
, то  .
.
4. Если  и
и  , то
, то  .
.
IV. Аксиома Архимеда.
1. Для любого  существует
существует  , удовлетворяющее неравенству
, удовлетворяющее неравенству  .
.
V. Аксиома непрерывности.
1. Для всякой системы вложенных числовых отрезков, стремящихся к нулю, существует единственное число, принадлежащее всем отрезкам данной системы. (Непрерывность в смысле Кантора).
Определение. Система числовых отрезков  ,
,  , …,
, …,  называется системой вложенных отрезков, если
называется системой вложенных отрезков, если  .
.
Определение.Длина вложенных отрезков  стремится к нулю, если
стремится к нулю, если  .
.
Теперь будем рассматривать только множества, состоящие из действительных чисел.
Определение.  (
(  - точная верхняя грань множества
- точная верхняя грань множества  ).
).
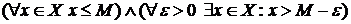
Определение.  (отрицание к предыдущему определению).
(отрицание к предыдущему определению).

Определение.Множество  ограничено сверху, если
ограничено сверху, если 
Определение.Множество  ограничено, если
ограничено, если 
Теорема. Всякое ограниченное сверху не пустое множество имеет точную верхнюю грань.
Доказательство.Внутри множества возьмем произвольную точку  . Это можно сделать, т. к. наше множество не пустое. Возьмем произвольную точку
. Это можно сделать, т. к. наше множество не пустое. Возьмем произвольную точку 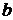 правее нашего множества. Это можно сделать, т. к. наше множество ограничено сверху. Отрезок
правее нашего множества. Это можно сделать, т. к. наше множество ограничено сверху. Отрезок  делим пополам и выбираем правый из половинок, содержащих точки множества
делим пополам и выбираем правый из половинок, содержащих точки множества  , или левый, если правый не содержит точек из
, или левый, если правый не содержит точек из  . Выбранный отрезок обозначаем
. Выбранный отрезок обозначаем  . Разбиваем отрезок
. Разбиваем отрезок  пополам и указанным способом выбираем отрезок
пополам и указанным способом выбираем отрезок  . Продолжая разбиения получим систему вложенных отрезков, длина которых стремится к нулю. Действительно,
. Продолжая разбиения получим систему вложенных отрезков, длина которых стремится к нулю. Действительно, 
|
|
|
Полученная система вложенных отрезков, стремящихся к нулю, в соответствие с аксиомой V, имеет общую точку  . Покажем, что
. Покажем, что  . Для этого надо показать, что выполняются два высказывания из определения супремума.
. Для этого надо показать, что выполняются два высказывания из определения супремума.
1).  . Предположим обратное. Пусть
. Предположим обратное. Пусть 
 . Тогда
. Тогда 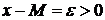 . Но при
. Но при  , т. е.
, т. е.  . Учитывая, что
. Учитывая, что  , последнее неравенство можно представить в виде:
, последнее неравенство можно представить в виде:  . Мы пришли к противоречию т. к.
. Мы пришли к противоречию т. к.  . Значит наше предположение не верно, т.е. первое высказывание выполняется.
. Значит наше предположение не верно, т.е. первое высказывание выполняется.
2).  . Действительно, т.к. длина отрезков стремится к нулю, то
. Действительно, т.к. длина отрезков стремится к нулю, то  Учитывая, что
Учитывая, что  и
и  , усилим последнее неравенство:
, усилим последнее неравенство:  . Мы получили:
. Мы получили:  .
.
Таким образом  . Теорема доказана.
. Теорема доказана.
Доказательство*.Заметим, что все отрезки содержат элементы множества, и правая точка отрезка лежит правее элементов множества или, по крайней мере, совпадает с правой точкой множества. Надо показать, что  , т.е. все элементы множества лежат левее
, т.е. все элементы множества лежат левее  или
или  является правой точкой множества, а также между точками множества и точкой
является правой точкой множества, а также между точками множества и точкой  отсутствует зазор.
отсутствует зазор.
Пусть какая-то точка  множества лежит правее точки
множества лежит правее точки  , тогда длина отрезка системы с номером
, тогда длина отрезка системы с номером  меньше расстояния между точкой
меньше расстояния между точкой  и точкой
и точкой  , т. е. точка
, т. е. точка  лежит правее точки
лежит правее точки  . Противоречие.
. Противоречие.
Предположим теперь наличие зазора между элементами множества и точкой  , тогда все отрезки системы не могут по длине быть меньше этого зазора, т.к. они содержат и точку
, тогда все отрезки системы не могут по длине быть меньше этого зазора, т.к. они содержат и точку  и хотя бы одну точку множества, что противоречит сходимости системы отрезков. Теорема доказана.
и хотя бы одну точку множества, что противоречит сходимости системы отрезков. Теорема доказана.
Числовая последовательность.
Определение.Числовая последовательность –бесконечное множество пронумерованных чисел. Каждый элемент последовательности характеризуется номером и своим значением.
Примеры последовательностей:  ;
;  ;
;  ;
; 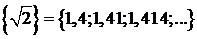 ;
;  .
.
Определение*.Числовая последовательность –функция, заданная на множестве натуральных чисел.
Определение.Последовательность неубывающая, если

Определение.Последовательность ограничена сверху, если

Определение.Последовательность не ограничена сверху, если (отрицание к предыдущему определению)

Определение.Число  называется пределом последовательности
называется пределом последовательности  , если
, если

Это записывается 
Рассмотрим неравенство 
 - окрестность точки
- окрестность точки  размера
размера  (интервал с центром в точке
(интервал с центром в точке  и длиной
и длиной  ).
).
Определение*.  , если
, если

Теорема. Если  имеет предел, то он единственный.
имеет предел, то он единственный.
Доказательство. Пусть  имеет два предела
имеет два предела  и
и  . Возьмем
. Возьмем 


Мы получили, что начиная с номера  , который больше
, который больше  и
и  , все члены последовательности лежат в окрестности тоски
, все члены последовательности лежат в окрестности тоски  и в окрестности точки
и в окрестности точки  . Противоречие, т.к. окрестности точек
. Противоречие, т.к. окрестности точек  и
и  не пересекаются. Теорема доказана.
не пересекаются. Теорема доказана.
Теорема. Если  имеет конечный предел, то она ограничена.
имеет конечный предел, то она ограничена.
Доказательство. Пусть  . Возьмем
. Возьмем  найдем
найдем  Из последнего неравенства следует
Из последнего неравенства следует 
Пусть  наибольшее среди чисел
наибольшее среди чисел 
 … ,
… , 
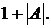 Тогда
Тогда  превосходит модуль всех членов нашей последовательности, т.е. последовательность ограничена. Теорема доказана.
превосходит модуль всех членов нашей последовательности, т.е. последовательность ограничена. Теорема доказана.
Определение. Последовательность, имеющая конечный предел, называется сходящейся последовательностью или фундаментальной последовательностью.
Теорема. Если 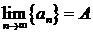 ,
, 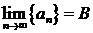 , то
, то
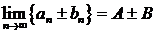 ;
;
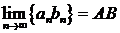 ;
;


Доказательство.Докажем выражение для произведения. Так как  имеет конечный предел, то она ограничена некоторым числом
имеет конечный предел, то она ограничена некоторым числом  . Пусть
. Пусть 
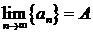

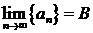
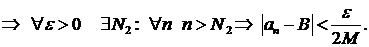
Для того чтобы доказать 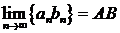 , надо показать, что для любого
, надо показать, что для любого  найдется номер
найдется номер  , такой, что для всех
, такой, что для всех  выполняется неравенство
выполняется неравенство 
 .
.
Начиная с любого номера  , который больше
, который больше  и
и  сумма в правой части неравенства меньше
сумма в правой части неравенства меньше  . Теорема доказана.
. Теорема доказана.
Пример. Показать, что  , где
, где  - геометрическая прогрессия при
- геометрическая прогрессия при  .
.
Заметим, что  . Так как
. Так как  , используя теорему о пределах суммы, произведения и частного, получаем требуемый результат.
, используя теорему о пределах суммы, произведения и частного, получаем требуемый результат.
Пример. Показать, что  .
.
Если  верное утверждение для числа
верное утверждение для числа  , тогда принцип математической индукции заключается в следующем:
, тогда принцип математической индукции заключается в следующем:  .
.
По индукции доказываем, что  . Делим числитель и знаменатель последовательности на
. Делим числитель и знаменатель последовательности на  и получаем нужный результат.
и получаем нужный результат.
Определение. Число  называется точной верхней гранью последовательности
называется точной верхней гранью последовательности 
 , если
, если  .
.
Теорема.Всякая ограниченная сверху последовательность  имеет предел, причем
имеет предел, причем  .
.
Доказательство. Так как последовательность ограничена сверху она имеет точную верхнюю грань  , значит
, значит  . В силу неубывания последовательности
. В силу неубывания последовательности  имеем:
имеем:  ;
;  ;
;  ;
;  . Таким образом,
. Таким образом,  , т.е.
, т.е.  Теорема доказана.
Теорема доказана.
Число  .
.
Покажем, что последовательность 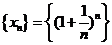 имеет предел. Для этого нодо показать, что она возрастающая и, что она ограничена сверху. Для преобразования
имеет предел. Для этого нодо показать, что она возрастающая и, что она ограничена сверху. Для преобразования 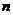 -го члена последовательности воспользуемся Биномом Ньютона:
-го члена последовательности воспользуемся Биномом Ньютона:



При увеличении 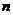 число слагаемых увеличивается, и каждое слагаемое увеличивается, значит, наша последовательность возрастающая. Далее имеем
число слагаемых увеличивается, и каждое слагаемое увеличивается, значит, наша последовательность возрастающая. Далее имеем
 , т.е. наша последовательность ограничена сверху. В последнем выражении мы использовали неравенство
, т.е. наша последовательность ограничена сверху. В последнем выражении мы использовали неравенство  , которое можно доказать методом математической индукции, а также формулу суммы геометрической прогрессии. Таким образом, наша последовательность имеет предел, который назвали числом
, которое можно доказать методом математической индукции, а также формулу суммы геометрической прогрессии. Таким образом, наша последовательность имеет предел, который назвали числом  .
.
Пусть задана последовательность  . Выберем из нее бесконечное число элементов с номерами
. Выберем из нее бесконечное число элементов с номерами  . Получим новую последовательность
. Получим новую последовательность  , которая называется подпоследовательностью последовательности
, которая называется подпоследовательностью последовательности  .
.
Теорема.(Больцано-Вейерштрасса). Из всякой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Доказательство. Так как  ограничена, то она принадлежит отрезку
ограничена, то она принадлежит отрезку  . Разделим его на две равные части. По крайней мере, один из них содержит бесконечное число элементов. Обозначим его через
. Разделим его на две равные части. По крайней мере, один из них содержит бесконечное число элементов. Обозначим его через  . Выберем какой-то элемент
. Выберем какой-то элемент  . Разделим
. Разделим  на две равные части, снова хотя бы один из них содержит бесконечное число элементов. Обозначим его
на две равные части, снова хотя бы один из них содержит бесконечное число элементов. Обозначим его 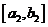 . Выберем какой-то элемент
. Выберем какой-то элемент  . Продолжим этот процесс. Получим систему вложенных отрезков и подпоследовательность
. Продолжим этот процесс. Получим систему вложенных отрезков и подпоследовательность  . Система вложенных отрезков стремится к нулю, следовательно имеет общую точку
. Система вложенных отрезков стремится к нулю, следовательно имеет общую точку  , к которой и сходится полученная подпоследовательность. Действительно
, к которой и сходится полученная подпоследовательность. Действительно  . Теорема доказана.
. Теорема доказана.
Теорема.(Критерий Коши). Для того чтобы последовательность сходилась (имела конечный предел) необходимо и достаточно чтобы она удовлетворяла условию Коши:  .
.
Доказательство. 1.(Необходимость). Пусть 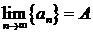 , тогда
, тогда  фундаментальна (удовлетворяет условию Коши).
фундаментальна (удовлетворяет условию Коши).
Имеем  Пусть
Пусть 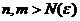 , тогда
, тогда  .
.
2. (Достаточность). Фундаментальная последовательность сходится (имеет конечный предел).
Сначала покажем, что фундаментальная последовательность ограничена. Пусть  , тогда, согласно условию Коши,
, тогда, согласно условию Коши,  , в частности
, в частности  . Так как
. Так как  , где
, где  , последовательность ограничена.
, последовательность ограничена.
Согласно теореме Больцано-Вейерштрасса, из ограниченной последовательности можно выбрать сходящуюся подпоследовательность  .
.
Пусть  . Имеем
. Имеем 
В силу фундаментальности этой последовательности 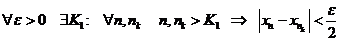 .
.
Если  , то
, то  , то есть
, то есть 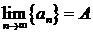 . Теорема доказана.
. Теорема доказана.
Пример.Покажем, что 
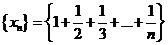 расходится.
расходится.
Запишем отрицание к условию Коши:  .
.
Пусть  , тогда
, тогда  . Таким образом,
. Таким образом,  , при котором выполняется отрицание условия Коши.
, при котором выполняется отрицание условия Коши.
Функции.
Каждому элементу множества  ставится в соответствие по некоторому закону
ставится в соответствие по некоторому закону  единственный элемент множества
единственный элемент множества  . Функция задается аналитически или графически. Монотонная функция имеет обратную функцию. Различают четные, нечетные и функции общего вида.
. Функция задается аналитически или графически. Монотонная функция имеет обратную функцию. Различают четные, нечетные и функции общего вида.
Определение.(По Коши)  , если
, если  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , быть может кроме самой этой точки, и если
, быть может кроме самой этой точки, и если  .
.
В определении предела удобно использовать вместо неравенств понятия окрестностей  .
.
Введем обозначения:
 - выколотая окрестность числа
- выколотая окрестность числа  размера
размера 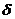 .
.
 - окрестность числа
- окрестность числа  размера
размера  .
.
 - окрестность
- окрестность  размера
размера  .
.
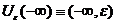 - окрестность
- окрестность  размера
размера  .
.
 - правая половины окрестности числа
- правая половины окрестности числа  размера
размера 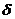 .
.
 - левая половины окрестности числа
- левая половины окрестности числа  размера
размера 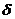 .
.
Определение.  , если
, если  определена на правой половине окрестности точки
определена на правой половине окрестности точки  , быть может кроме самой этой точки, и если
, быть может кроме самой этой точки, и если 
Определение*.(По Гейне)  , если
, если  .
.
Теорема. Определения по Коши и по Гейне эквивалентны.
Пример. Доказать по определению  .
.
Запишем определение:  . Когда значения нашей функции принадлежат
. Когда значения нашей функции принадлежат  , аргумент
, аргумент  принадлежит интервалу
принадлежит интервалу  . Нам необходимо найти максимальный размер окрестности
. Нам необходимо найти максимальный размер окрестности  принадлежащий указанному интервалу. Окрестность
принадлежащий указанному интервалу. Окрестность  - интервал симметричный относительно числа 2. Используя график функции и изображения окрестностей, находим, что
- интервал симметричный относительно числа 2. Используя график функции и изображения окрестностей, находим, что  .
.
Пример. Доказать, что  .
.
Сформулируем отрицание к определению предела по Гейне:  . Оно выполняется для последовательности
. Оно выполняется для последовательности  , которая сходится к нулю, а последовательность
, которая сходится к нулю, а последовательность  не имеет конечного предела (можно показать при помощи Критерия Коши).
не имеет конечного предела (можно показать при помощи Критерия Коши).
Теорема. Если  , где
, где  - конечное число, то на некоторой окрестности
- конечное число, то на некоторой окрестности 
 -ограничена, то есть
-ограничена, то есть  .
.
Доказательство. Пусть  , тогда
, тогда 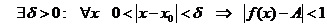 . Преобразуем последнее неравенство:
. Преобразуем последнее неравенство: 
 . Отсюда имеем, что для любого
. Отсюда имеем, что для любого  , т.е. функция ограничена числом
, т.е. функция ограничена числом  . Теорема доказана.
. Теорема доказана.
Теорема.(О сохранении знака). Если  , где
, где  - конечное число, то на некоторой окрестности
- конечное число, то на некоторой окрестности 
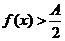 , если
, если  , и
, и  , если
, если  .
.
Доказательство. Пусть  , тогда
, тогда  . Последнее неравенство запишем в виде:
. Последнее неравенство запишем в виде:  . Если
. Если  , то из левого неравенства имеем
, то из левого неравенства имеем  . Если
. Если  , то из правого неравенства имеем
, то из правого неравенства имеем  . Теорема доказана.
. Теорема доказана.
Теорема.(О зажатой функции). Если  ,
, 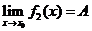 и на некоторой окрестности
и на некоторой окрестности 
 , тогда
, тогда  .
.
Доказательство. Используя последнее неравенство и определения пределов функций  и
и  , запишем:
, запишем:  . Из этого выражения следует, что для
. Из этого выражения следует, что для  и
и  выполняется неравенство
выполняется неравенство 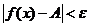 . Таким образом,
. Таким образом,  . Теорема доказана.
. Теорема доказана.
Теорема. Пусть  и
и  , тогда:
, тогда:
1)  ;
;
2)  ;
;
3)  .
.
Теорема легко доказывается с использованием определения предела по Гейне и аналогичной теоремы для последовательностей.
Теорема. (Критерий Коши). Для того, чтобы существовал конечный предел 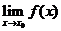 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  была определена в некоторой окрестности точки
была определена в некоторой окрестности точки  , быть может кроме самой этой точки, и
, быть может кроме самой этой точки, и  .
.
(Без доказательства).
Непрерывность функции.
Определение. Функция  непрерывна в точке
непрерывна в точке  , если она определена в некоторой окрестности этой точки, в том числе и в самой тоске
, если она определена в некоторой окрестности этой точки, в том числе и в самой тоске  , и если
, и если  , т.е.
, т.е.  .
.
Из определения следует, что для непрерывной функции справедливо равенство:
 , то есть предел можно вносить в аргумент непрерывной функции.
, то есть предел можно вносить в аргумент непрерывной функции.
Определение*. Функция  непрерывна в точке
непрерывна в точке  , если она определена в некоторой окрестности этой точки, в том числе и в самой тоске
, если она определена в некоторой окрестности этой точки, в том числе и в самой тоске  , и если ее приращение в этой точке, соответствующее приращению аргумента
, и если ее приращение в этой точке, соответствующее приращению аргумента  , стремится к нулю при
, стремится к нулю при  , т.е.
, т.е.  .
.
Пример. Функция  непрерывна для любого
непрерывна для любого  .
.
Действительно  .
.
Пример. Функция  непрерывна для любого
непрерывна для любого  .
.
 . Здесь мы использовали неравенство
. Здесь мы использовали неравенство  . Таким образом, имеем
. Таким образом, имеем  , т.е. функция
, т.е. функция  зажата между двумя функциями, стремящимися к нулю. Значит, и
зажата между двумя функциями, стремящимися к нулю. Значит, и  стремится к нулю.
стремится к нулю.
Теорема. Если  и
и  непрерывны в точке
непрерывны в точке  , то непрерывны их сумма, разность, произведение и частное.
, то непрерывны их сумма, разность, произведение и частное.
Доказательство. Доказательство вытекает из определения непрерывности  и теоремы о пределах суммы, разности, произведения и частного.
и теоремы о пределах суммы, разности, произведения и частного.
Теорема. (О непрерывности сложной функции). Пусть задана функция  , непрерывная в точке
, непрерывная в точке  , и функция
, и функция  , непрерывная в точке
, непрерывная в точке  , и пусть
, и пусть  . Тогда сложная функция
. Тогда сложная функция  непрерывна в точке
непрерывна в точке  .
.
Доказательство.  .
.
Пример. Многочлен  - непрерывная функция, т.к. является результатом конечного числа арифметических операций над непрерывной функцией
- непрерывная функция, т.к. является результатом конечного числа арифметических операций над непрерывной функцией 
Пример.  - сложная функция.
- сложная функция.
Пример.  - непрерывная функция.
- непрерывная функция.
Действительно:  ;
;  .
.
Пример. Если  непрерывна, то непрерывна и сложная функция
непрерывна, то непрерывна и сложная функция  .
.
Замечательные пределы.
 - первый замечательный предел.
- первый замечательный предел.
Используя тригонометрический круг, определение синуса и тангенса, а также неравенство  , можно при
, можно при  записать выражение
записать выражение  . Разделим его на
. Разделим его на  и получим
и получим  . По теореме о зажатой функции имеем
. По теореме о зажатой функции имеем  .
.
 - второй замечательный предел.
- второй замечательный предел.
Для натуральной переменной следует из определения числа  . Можно показать, что переменной может быть не только натуральное число, но и действительное число, стремящееся к
. Можно показать, что переменной может быть не только натуральное число, но и действительное число, стремящееся к  . Кроме того, если сделать замену переменной
. Кроме того, если сделать замену переменной  , то получим эквивалентную запись этого предела
, то получим эквивалентную запись этого предела  .
.
Классификация точек разрывов.
Разрывы бывают устранимые и неустранимые. Отличают неустранимые разрывы первого и второго рода.
Функция  в точке
в точке  имеет устранимый разрыв, если предел слева равен пределу справа и не равен значению функции в точке
имеет устранимый разрыв, если предел слева равен пределу справа и не равен значению функции в точке  . Такой разрыв можно устранить, изменив значение функции в одной точке. Пример:
. Такой разрыв можно устранить, изменив значение функции в одной точке. Пример:  .
.
Функция  в точке
в точке  имеет неустранимый разрыв первого рода, если конечный предел слева не равен конечному пределу справа. Пример:
имеет неустранимый разрыв первого рода, если конечный предел слева не равен конечному пределу справа. Пример:  .
.
Функция  в точке
в точке  имеет неустранимый разрыв второго рода, если хотя бы один из пределов не существует или равен
имеет неустранимый разрыв второго рода, если хотя бы один из пределов не существует или равен  . Примеры:
. Примеры:  ;
;  .
.
Сравнение бесконечно малых.
Определение.Если  , то говорят, что
, то говорят, что  бесконечно малая при
бесконечно малая при  .
.
Определение.Если  и
и  - бесконечно малая при
- бесконечно малая при  и
и  , то говорят, что
, то говорят, что  - о- малое от
- о- малое от  при
при  , т.е.
, т.е.  при
при  .
.
Определение.Если  , где
, где  - конечное число, то говорят, что
- конечное число, то говорят, что  и
и  величины одного порядка малости при
величины одного порядка малости при  .
.
Определение.Если  ,
,  эквивалентна
эквивалентна  при
при  , т.е.
, т.е.  при
при  .
.
Примеры эквивалентных бесконечно малых при  :
:  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
Определение.Если  , то говорят, что
, то говорят, что  бесконечно большая величина при
бесконечно большая величина при  .
.
Функции, непрерывные на отрезке.
Определение.Функция  непрерывна на отрезке
непрерывна на отрезке  , если она непрерывна во всех точках интервала
, если она непрерывна во всех точках интервала  , а
, а  и
и  .
.
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она ограничена, т.е.
, то она ограничена, т.е.  .
.
Доказательство. Допустим, что функция  не ограничена на отрезке
не ограничена на отрезке  . Тогда
. Тогда  . Берем последовательно
. Берем последовательно  , получим:
, получим:  . Заметим, что
. Заметим, что  . Последовательность
. Последовательность  ограничена, т.к.
ограничена, т.к.  . По теореме Больцано-Вейерштрасса из
. По теореме Больцано-Вейерштрасса из  можно выбрать сходящуюся подпоследовательность
можно выбрать сходящуюся подпоследовательность  , т.е.
, т.е.  , где
, где  . В силу непрерывности
. В силу непрерывности  имеем:
имеем:  , где
, где  конечное число, согласно нашему предположению. Но мы уже получили, что
конечное число, согласно нашему предположению. Но мы уже получили, что  , а значит,
, а значит,  . Противоречие. Теорема доказана.
. Противоречие. Теорема доказана.
Теорема. (Вейерштрасса). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то существует ее минимум и максимум на
, то существует ее минимум и максимум на  , т.е. существуют точки
, т.е. существуют точки  .
.
Доказательство. Докажем для максимума. По предыдущей теореме непрерывная на отрезке  функция ограничена сверху некоторым числом
функция ограничена сверху некоторым числом  , но тогда существует точная верхняя грань
, но тогда существует точная верхняя грань 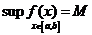 , т.е.
, т.е.  . Полагая последовательно
. Полагая последовательно 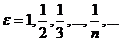 , получаем последовательность
, получаем последовательность  , такую, что
, такую, что 

 . Так как последовательность
. Так как последовательность  ограничена, то существует подпоследовательность
ограничена, то существует подпоследовательность  сходящаяся к
сходящаяся к  . В силу непрерывности нашей функции
. В силу непрерывности нашей функции  . Если предел существует, то он единственный, т.е.
. Если предел существует, то он единственный, т.е.  .
.
Таким образом, точная верхняя грань достигается функцией в точке  , т.е. в точке
, т.е. в точке  функция принимает свое максимальное значение. Теорема доказана.
функция принимает свое максимальное значение. Теорема доказана.
Теорема. (О нулях непрерывной на отрезке функции). Если функция  непрерывна на отрезке
непрерывна на отрезке  и принимает на его концах значения разных знаков, то на интервале
и принимает на его концах значения разных знаков, то на интервале  имеется, по крайней мере, одна точка
имеется, по крайней мере, одна точка  , такая, что
, такая, что  .
.
Доказательство. Обозначим отрезок  через
через 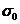 . Разделим его пополам. Если в середине
. Разделим его пополам. Если в середине 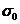 функция равна нулю, то теорема доказана. Если этого нет, то одна из половинок такая, что на концах функция имеет значения разных знаков. Обозначим именно эту половинку через
функция равна нулю, то теорема доказана. Если этого нет, то одна из половинок такая, что на концах функция имеет значения разных знаков. Обозначим именно эту половинку через  . Продолжим эту процедуру. Мы либо наткнемся на точку
. Продолжим эту процедуру. Мы либо наткнемся на точку  , такую, что
, такую, что  , либо получим систему вложенных стремящихся к нулю отрезков. Система таких отрезков по аксиоме непрерывности имеет общую точку
, либо получим систему вложенных стремящихся к нулю отрезков. Система таких отрезков по аксиоме непрерывности имеет общую точку  . Покажем, что
. Покажем, что  .
.
Пусть, например,  . Но тогда по теореме о сохранении знака непрерывной функции
. Но тогда по теореме о сохранении знака непрерывной функции  . С другой стороны, для
. С другой стороны, для  мы можем указать вложенный отрезок
мы можем указать вложенный отрезок  , где
, где  принимает разные знаки на концах отрезка. Противоречие.
принимает разные знаки на концах отрезка. Противоречие.
Предположение  тоже приводит к противоречию. Тогда по аксиоме порядка
тоже приводит к противоречию. Тогда по аксиоме порядка  . Теорема доказана.
. Теорема доказана.
Вопросы к коллоквиуму по математическому анализу (1 семестр)
1.Множество действительных чисел.
2.Теорема о точной грани ограниченного множества.
3.Понятие числовой последовательности. Ее предел.
4.Единственность предела. Ограниченность сходящейся последовательности.
5.Арифметические операции над сходящимися последовательностями.
6.Точная верхняя грань последовательности. Теорема о пределе ограниченной сверху неубывающей последовательности.
7.Число е.
8.Теорема Больцано-Вейерштрасса.
9.Критерий Коши существования конечного предела последовательности.
10.Понятие функции действительного переменного. Предел функции.
11.Эквивалентность определений предела по Коши и по Гейне.
12. Критерий Коши существования предела функции.
13.Теорема об ограниченности функции, имеющей конечный предел.
14.Теорема о сохранении знака функции, имеющей конечный предел.
15.Теорема о зажатой функции.
16.Непрерывность функции. Непрерывность сложной функции.
17.Классификация точек разрыва. Примеры.
18.Замечательные пределы.
19.Сравнение бесконечно малых.
20.Ограниченность функции, непрерывной на отрезке.
21.Теорема Вейерштрасса.
22.Теорема о нулях непрерывной на отрезке функции.

Дата добавления: 2018-02-18; просмотров: 712; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
