Лопиталь ережесі. Функцияны зерттеу
Дәріс. Дифференциалдау теориясы және оның кейбір қолданулары. Элементар функцияларды дифференциалдау. Туынды, туындысы бар болатын функцияның үзіліссіздігі. Дифференциалдау ережелері. Функция туындысы және дифференциалы. Күрделі, кері және параметрлік түрде, айқындалмаған түрде берілген функцияларды дифференциалдау. Локальды экстремум. Функцияның ең үлкен және ең кіші мәндері. Функцияны туындының көмегімен зерттеу. Функцияның экстремумдары. Дөңес функциялар. Асимптоталар. Ойыс-дөңестік. Функцияны туындының көмегімен толық зерттеп, графигін тұрғызу. Функцияның туындысы маңайында, нүктесін қоса алғанда, функциясы берілсін. нүктесінде аргументіне өсімшесін береміз. (оң немесе теріс). Онда . Анықтама 1. Егер шегі табылса, онда оны нүктесіндегі функциясының туындысы деп айтамыз, немесе функциясы нүктесінде дифференциалданады деп айтамыз және былай белгілейміз: яғни, (1) Егер (1)-де және болса, онда (1)-ді нүктесіндегі оң жақ туындысы [ сол жақ туындысы] деп атаймыз. Егер және , онда . Анықтама 2. функциясын кесіндісінде дифференциалданады деп айтамыз, егер оның аралығындағы әрбір нүктеде туындысы бар болса, ал және ұштарында сәйкесінше және табылса. облысында дифференциалданатын функциялардың класын деп белгілейміз. Туындының механикалық және геометриялық мағынасы а) Механикалық. - нүктесінің қозғалу заңы болсын. нүктесінің -дан -ға дейінгі аралығындағы қозғалысын қарастыралық. Онда ал - орташа жылдамдық. Егер , шегі табылса, онда жолдың уақыт бойынша туындысы нүктесінің уақыт аралығындағы қозғалысының жылдамдығына тең. 12-сурет б) Геометриялық. қисығында және нүктелерін қарастыралық. және екендігі анық. нүктесін қисықтың бойымен нүктесіне қарай жылжытамыз. нүктесінің орналасу аралығын белгілей отырып, қимасын аламыз. Онда болған жағдайда болатыны анық. Анықтама 3. нүктесі қисықтың бойымен нүктесіне кез келген жағынан шексіз жақындағанда қимасының шектелген орны табылса, онда қисығына нүктесінде жүргізілген жанама деп аталады. Егер қисықтың жанамасы бар болса, онда . Бұдан, нүктесінде дифференциалданатын функцияның осы нүктеде бұрыштық коэффициенті болатын жанамасы бар болады. Мысал 1. функциясының нүктесіндегі жанамасының теңдеуін жаз. а) . болғандықтан, жанаманың теңдеуі . -ті табалық: б) . болғандықтан, және жанаманың теңдеуі . в) 13-сурет 14-сурет Оң жақ жанамасы болады, яғни , ал сол жағынан жанамасы , яғни . Бұдан, нүктесінде берілген функцияның туындысы табылмайды, бұл функция нүктесінде үзіліссіз болғанның өзінде. болатын нүктелер бұрыштық деп аталады.
|
|
|
|
|
|
Теоремалар.
1. Егер  функциясы
функциясы  нүктесінде дифференциалданатын болса, онда бұл функция осы нүктеде үзіліссіз.
нүктесінде дифференциалданатын болса, онда бұл функция осы нүктеде үзіліссіз.
Шынымен де,  мұндағы
мұндағы  , егер
, егер  . Бұдан,
. Бұдан,
 , егер
, егер  .
.
2. Күрделі функциялардың туындылары.Егер  функциясы
функциясы  нүктесінде диф-ференциалданатын, ал
нүктесінде диф-ференциалданатын, ал  функциясы
функциясы  нүктесінде дифференциалданатын болса, онда
нүктесінде дифференциалданатын болса, онда  күрделі функциясы
күрделі функциясы  нүктесінде дифференциалданады және
нүктесінде дифференциалданады және
 , немесе
, немесе 
3. Кері функцияның туындысы.Егер  функциясы үшін
функциясы үшін  нүктесінде туындысы бар және ол нөлден өзгеше болатындай
нүктесінде туындысы бар және ол нөлден өзгеше болатындай  кері функциясы табылса, онда
кері функциясы табылса, онда
 .
.
4.  және
және  табылсын, ал
табылсын, ал  - const. Онда
- const. Онда
|
|
|
1. а)  . Шынында да,
2. . Шынында да,
2.  .
б) .
б)  . .
| 3. в)  .
г) .
г)  . .
|
Туындының кестесі
 -
-  айнымалысына тәуелді функциялар, ал
айнымалысына тәуелді функциялар, ал  - тұрақты сандар болсын. Онда
- тұрақты сандар болсын. Онда

3-формуланың дәлелдеуін келтірелік.

Мысал 2. Берілген функциялардың туындыларын тап:
а)  . 2-ші формуладан
. 2-ші формуладан  .
.
б)  .
.  . 2-ші формуладан
. 2-ші формуладан  .
.
в)  .
.  . 2-ші формуладан
. 2-ші формуладан  .
.
г)  . 11-ші формуладан
. 11-ші формуладан  .
.
 айқын емес функциясын дифференциалдау
айқын емес функциясын дифференциалдау
Берілген функцияның туындысын табу үшін  -тің
-тің  айнымалысына тәуелді функция екенін ескере отырып, теңдіктің екі жағын да дифференциалдаймыз.
айнымалысына тәуелді функция екенін ескере отырып, теңдіктің екі жағын да дифференциалдаймыз.
Мысал 3.  функциясының туындысын тап.
функциясының туындысын тап.

Параметрлік түрде берілген функцияның туындысы
 айнымалысына тәуелді
айнымалысына тәуелді  функциясы параметрлік түрде берілсін
функциясы параметрлік түрде берілсін
 .
.
 функциясының кері функциясы бар болып,
функциясының кері функциясы бар болып,  және
және  функциялары дифференциалданатын функциялар, сонымен қатар,
функциялары дифференциалданатын функциялар, сонымен қатар,  болсын. Онда
болсын. Онда  .
.
Мысал 4.  тап.
тап. 

Функцияның дифференциалы
 болсын. Онда
болсын. Онда  мұндағы
мұндағы  , егер
, егер  . Бұдан
. Бұдан  .
.
 болсын. Онда
болсын. Онда  теңдіктерден төмендегі теңдікті аламыз:
теңдіктерден төмендегі теңдікті аламыз:
1.  2.
2.  3.
3. 
| 4.  немесе немесе  болсын. Онда болсын. Онда
 - бірінші дифферен-циалдың формасының инварианттылық қасиеті.
5. - бірінші дифферен-циалдың формасының инварианттылық қасиеті.
5.  болса. болса.  теңдігі орынды болғандық-
тан, жуықтап есептеуде теңдігі орынды болғандық-
тан, жуықтап есептеуде 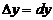 деп алуға болады, немесе деп алуға болады, немесе
|
 (5)
(5)
|
|
|
Мысал 5.  есепте.
есепте.
 функциясын қарастыралық және
функциясын қарастыралық және  деп алайық.
деп алайық.  ретінде
ретінде  санын аламыз. Онда
санын аламыз. Онда 
 .
.
 . Онда (5)-тен
. Онда (5)-тен  .
.
Туынды және жоғарғы дифференциалдар
 болсын. Егер
болсын. Егер  болса, онда
болса, онда 
 функциясының екінші ретті туындысы деп аталады және былай белгіленеді:
функциясының екінші ретті туындысы деп аталады және былай белгіленеді:  . Яғни
. Яғни
 немесе
немесе 
Анықтама 5.  функциясының
функциясының  -ші ретті туындысы деп
-ші ретті туындысы деп  -ші ретті туындыдан алынған туындыны айтамыз, яғни,
-ші ретті туындыдан алынған туындыны айтамыз, яғни,

Мысал 6. 
 болсын. Онда
болсын. Онда 
 функциясының екінші ретті диф-ференциалы деп аталады. Бұдан
функциясының екінші ретті диф-ференциалы деп аталады. Бұдан
 .
.
Анықтама 6.  функциясының
функциясының  -ші ретті дифференциалы деп
-ші ретті дифференциалы деп  -ші ретті дифференциалды тағы бір рет дифференциалдауды айтамыз және
-ші ретті дифференциалды тағы бір рет дифференциалдауды айтамыз және
 (6)
(6)
(6)-дан
 (7)
(7)
шығады. (6) және (7) теңдіктер  айнымалысы тәуелсіз айнымалы болған жағдайда ғана ақиқат.
айнымалысы тәуелсіз айнымалы болған жағдайда ғана ақиқат.
 болсын. Онда
болсын. Онда  .
.
 ,
,
яғни, дифференциалдың формасының инварианттылығы сақталмайды.
Лопиталь ережесі. Функцияны зерттеу
Анықтама. Егер  деген сан табылып,
деген сан табылып,  нүктенiң
нүктенiң  маңайындағы барлық
маңайындағы барлық  үшiн мына теңсiздiк орындалса
үшiн мына теңсiздiк орындалса

онда 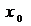 нүктесi
нүктесi  функцияның төңiректiк максимум (минимум) нүктесi деп аталады, Функцияның төңiректiк максимумы немесе минимумы функцияның төңiректiк экстремумы деп аталады.
функцияның төңiректiк максимум (минимум) нүктесi деп аталады, Функцияның төңiректiк максимумы немесе минимумы функцияның төңiректiк экстремумы деп аталады.
Мысалы 57-суреттегi  - төңiректiк минимум нүктелерi, ал
- төңiректiк минимум нүктелерi, ал  - төңiрек-тiк максимум нүктелерi, ал
- төңiрек-тiк максимум нүктелерi, ал  және
және  - бiржақты төңiректiк экстремум нүкте-лерi.
- бiржақты төңiректiк экстремум нүкте-лерi.
1. Ферма теоремасы.  интервалында анықталған
интервалында анықталған  функция-ның
функция-ның  нүктеде төңiректiк экстремум болсын. Егер бұл функцияның
нүктеде төңiректiк экстремум болсын. Егер бұл функцияның  нүктеде шенелген туындысы
нүктеде шенелген туындысы  бар болса, онда
бар болса, онда  болады.
болады.
2. Ролль теоремасы.  функциясы 1)
функциясы 1)  кесiндiсiнде үзiлiссiз; 2)
кесiндiсiнде үзiлiссiз; 2)  интервалдың әрбiр нүктесiнде дифференциалданатын; 3)
интервалдың әрбiр нүктесiнде дифференциалданатын; 3)  болса, онда
болса, онда  интервалынан
интервалынан  болатын ең кем дегенде бiр
болатын ең кем дегенде бiр  нүктесi табылады.
нүктесi табылады.
3. Коши теоремасы. 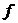 және
және  функциялары 1)
функциялары 1)  кесiндiсiнде үзiлiссiз; 2)
кесiндiсiнде үзiлiссiз; 2)  интервалдың әрбiр нүктесiнде туындылары бар; 3)
интервалдың әрбiр нүктесiнде туындылары бар; 3)  интервалдың барлық нүктелерiнде
интервалдың барлық нүктелерiнде  болса, онда
болса, онда  нүктесi табылып
нүктесi табылып



теңдiк орындалады.
4. Лагранж теоремасы.(Орта мән туралы теорема).  функциясы
функциясы  кесiндiсiнде үзiлiссiз және
кесiндiсiнде үзiлiссiз және  интервалдың әрбiр нүктесiнде туын-дысы болса, онда осы интервалдан ең кемiнде бiр
интервалдың әрбiр нүктесiнде туын-дысы болса, онда осы интервалдан ең кемiнде бiр  нүктесi табылып, мына теңдiк орындалады
нүктесi табылып, мына теңдiк орындалады
Лопиталь ережесi
 түрiндегi анықталмағандықтарды есептеуге Лопиталь ережесi жиi қолданылады.
түрiндегi анықталмағандықтарды есептеуге Лопиталь ережесi жиi қолданылады.
1-теорема.  және
және  функциялары
функциялары  нүктенiң кейбiр аймағында, мүм-кiн
нүктенiң кейбiр аймағында, мүм-кiн  нүктеден басқа барлық нүктелерiнде, үзiлiссiз және олардың туынды-лары бар болсын. Осы көрсетiлген аймақта
нүктеден басқа барлық нүктелерiнде, үзiлiссiз және олардың туынды-лары бар болсын. Осы көрсетiлген аймақта  және
және  болып,
болып,

теңдiктерi орындалсын, Егер  бар болса, онда
бар болса, онда  бар болады және мына теңдiк орындалады
бар болады және мына теңдiк орындалады 
Мысал. 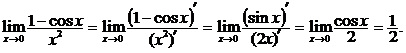
2-теорема.  және
және  функциялары
функциялары  кейбiр аймағында үзiлiссiз және туындылары бар болсын және
кейбiр аймағында үзiлiссiз және туындылары бар болсын және

Осы аймақта  және
және  нөлге тең болмасын, яғни
нөлге тең болмасын, яғни  Егер
Егер  бар болса, онда
бар болса, онда  бар болады және мына теңдiк орында-лады
бар болады және мына теңдiк орында-лады

Дифференциалданатын функциялардың тұрақтылығы,өсуі және кемуі
1-теорема. (функцияның тұрақтылығының критериi)  функциясы
функциясы
1) берілген кейбір ақырлы немесе ақырсыз аралықта анықталсын;
2) осы аралықтың барлық ішкі нүктелерiндегi туындысы нөл болсын;
3) осы аралықтың соңғы нүктелерiнде үзіліссіз болсын.
Онда  функциясы осы аралықта тұрақты.
функциясы осы аралықта тұрақты.
2-теорема. (Функцияның өсуiнiң критериi).
 кесіндіде
кесіндіде  функциясы үзілiссiз және
функциясы үзілiссiз және  аралығында туындылары теріс емес (оң) болсын, онда функция бұл кесiндiде кемімейді (өседi).
аралығында туындылары теріс емес (оң) болсын, онда функция бұл кесiндiде кемімейді (өседi).
3-теорема.(Функцияның кемуiнiң критериi).
Егер  кесiндiде
кесiндiде  функциясы үзілiссiз және
функциясы үзілiссiз және  -да
-да  болса, онда
болса, онда  функциясы
функциясы  кесiндiде өспейді (кемидi).
кесiндiде өспейді (кемидi).
Анықтама. Егер  оң саны табылып, функцияның өсімшесі мына теңсiздiкті
оң саны табылып, функцияның өсімшесі мына теңсiздiкті  (немесе
(немесе  ) қанағаттандырса, онда
) қанағаттандырса, онда 
 функцияның төңiректiк максимум (минимум) нүктесі дейді.
функцияның төңiректiк максимум (минимум) нүктесі дейді.
Төңiректiк максимум және минимум нүктелері төңiректiк экстремум нүктелері деп аталынады.
1. Экстремумның қажетті шарты.
Егер  нүктесі
нүктесі  функцияның төңiректiк экстремум нүктесі болса, онда Ферма теоремасы бойынша оның осы нүктедегі туындысы нөлге тең, яғни
функцияның төңiректiк экстремум нүктесі болса, онда Ферма теоремасы бойынша оның осы нүктедегі туындысы нөлге тең, яғни 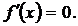 Функцияның туындысы нөл болатын нүктелерді стационар нүктелер деп атайды.
Функцияның туындысы нөл болатын нүктелерді стационар нүктелер деп атайды.
2. Төңiректiк экстремумның жеткілікті критерилерi.
1-теорема.  нүктесі
нүктесі  функцияның стационар нүктесi болсын (яғни
функцияның стационар нүктесi болсын (яғни  ) және
) және  функцияның
функцияның  нүктенiң кейбір маңайында үзiлiссiз екінші ретті туындысы болсын
нүктенiң кейбір маңайында үзiлiссiз екінші ретті туындысы болсын
1) егер  болса, онда
болса, онда  нүктесі төңiректiк максимум нүктесi болады;
нүктесі төңiректiк максимум нүктесi болады;
2) егер  болса, онда
болса, онда  нүктесі төңiректiк минимум нүктесi болады.
нүктесі төңiректiк минимум нүктесi болады.
Мысал.  функцияның төңiректiң экстремум нүктесiн табу
функцияның төңiректiң экстремум нүктесiн табу
керек.
3. Функцияның ең үлкен және ең кіші мәндері
 кесiндiде үзiлiссiз
кесiндiде үзiлiссiз  функцияның максимум (минимум) болатын нүктелерін табу керек. Бұл функция
функцияның максимум (минимум) болатын нүктелерін табу керек. Бұл функция  нүктеде өзiнiң максимумына (минимумына) мына үш жағдайда ғана жетеді:
нүктеде өзiнiң максимумына (минимумына) мына үш жағдайда ғана жетеді:
1)  2)
2)  3)
3) 
Егер  болса, онда
болса, онда  төңiректiк экстремум нүктесi болады, оны стационар нүктелердiң ішінен немесе туындысы болмайтын нүктелердің ішінен іздеу керек. Бұл нүктелер
төңiректiк экстремум нүктесi болады, оны стационар нүктелердiң ішінен немесе туындысы болмайтын нүктелердің ішінен іздеу керек. Бұл нүктелер  ақырлы жиын құрсын, онда
ақырлы жиын құрсын, онда

[pr] Мысал.  функцияның
функцияның  кесiндiдегi ең үлкен және ең кiшi мәндерiн табу керек.
кесiндiдегi ең үлкен және ең кiшi мәндерiн табу керек.
Шешімі. 
Егер  нүктеде
нүктеде  кесiндiде жатады, ал қалған нүктелер бұл кесiндiде жатпайды. Сонымен
кесiндiде жатады, ал қалған нүктелер бұл кесiндiде жатпайды. Сонымен 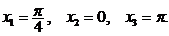


Функцияның дөңестігі және ойыстығы. Иілу нүктелері.
1-анықтама.  нүктеде
нүктеде  қисықты дөңес (ойыс) дейміз, егер
қисықты дөңес (ойыс) дейміз, егер  нүктенiң қайсiбiр төңiрегі табылып, осы төңiректiң барлық нүктелерiнде
нүктенiң қайсiбiр төңiрегі табылып, осы төңiректiң барлық нүктелерiнде  нүктеден қисыққа жүргізілген жанама осы қисықтан жоғары (төмен) орналасқан болса.
нүктеден қисыққа жүргізілген жанама осы қисықтан жоғары (төмен) орналасқан болса.
2-анықтама.  нүктесi
нүктесi  қисықтың иілу нүктесі деп аталады, егер
қисықтың иілу нүктесі деп аталады, егер 
 арқылы өткенде қисықтың нүктелері
арқылы өткенде қисықтың нүктелері  нүкте-сiнде жүргізілген жанаманың бір жағынан екінші жағына өтсе.
нүкте-сiнде жүргізілген жанаманың бір жағынан екінші жағына өтсе.
1-теорема. (Функцияның дөңестiгiнiң критериi).
Егер  функцияның
функцияның  нүктедегiекінші ретті үзiлiссiзтуындысы болса және
нүктедегiекінші ретті үзiлiссiзтуындысы болса және  болса, онда бұл қисық
болса, онда бұл қисық  нүктеде ойыс(дөңес) болады.
нүктеде ойыс(дөңес) болады.
Салдар. Егер  нүктесi
нүктесi  қисықтың иілу нүктесi болса және
қисықтың иілу нүктесi болса және  нүктеде функцияның екінші ретті туындысы болса, онда ол туынды нөлге тең, яғни
нүктеде функцияның екінші ретті туындысы болса, онда ол туынды нөлге тең, яғни 
2-теорема. Егер  функцияның
функцияның  нүктедегі үшінші ретті туындысы
нүктедегі үшінші ретті туындысы  үзiлiссiз болса, ал
үзiлiссiз болса, ал  және
және  болмаса, онда
болмаса, онда  нүктесі
нүктесі  функциясының иілу нүктесі болады.
функциясының иілу нүктесі болады.
Функцияның графигiнiң асимптоталары
Кейбiр жағдайда функцияның графигi,  және
және  ұмтылған-да немесе екiншi типтi үзiлiс нүктелердiң маңында, қайсiбiр түзуге ақырсыз жақындай түседi. Осындай түзулердi қисықтың асимптоталары деп атайды.
ұмтылған-да немесе екiншi типтi үзiлiс нүктелердiң маңында, қайсiбiр түзуге ақырсыз жақындай түседi. Осындай түзулердi қисықтың асимптоталары деп атайды.
Асимптоталардың үш түрi болады: тiк асимптота, горизонталь асимп-тота және көлбеу асимптота.
1-анықтама. Егер  ұмтылғанда функцияның бiржақты шектерiнiң кем дегенде бiреуi шексiздiкке ұмтылса, яғни
ұмтылғанда функцияның бiржақты шектерiнiң кем дегенде бiреуi шексiздiкке ұмтылса, яғни  болса, онда
болса, онда  түзуi
түзуi  қисығының тiк асимптотасы деп аталады.
қисығының тiк асимптотасы деп аталады.
2-анықтама. Егер  немесе
немесе  ұмтылғанда
ұмтылғанда  функцияның ақырлы шегi бар болса, яғни
функцияның ақырлы шегi бар болса, яғни 
болса, онда  түзуiн
түзуiн  функциясының горизонталь асимптотасы деп атайды.
функциясының горизонталь асимптотасы деп атайды.
3-анықтама. Егерде  функциясын мына түрде жазуға болатын болса
функциясын мына түрде жазуға болатын болса


онда  ұмтылғанда
ұмтылғанда  түзуi
түзуi  функцияның көлбеу асимптотасы деп аталады.
функцияның көлбеу асимптотасы деп аталады.
Теорема.  ұмтылғанда
ұмтылғанда  түзуi
түзуi  функциясының графигiнiң көлбеу асимптотасы болу үшiн, мына шектердiң болуы қажеттi және жеткiлiктi
функциясының графигiнiң көлбеу асимптотасы болу үшiн, мына шектердiң болуы қажеттi және жеткiлiктi



Қажеттiлiгi.  ұмтылғанда
ұмтылғанда 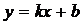 түзуi
түзуi  функциясының көлбеу асимптотасы болсын, онда
функциясының көлбеу асимптотасы болсын, онда  теңдiк орындалады, содан
теңдiк орындалады, содан


Жеткiлiктiлiгi.  шектер бар болсын. Онда шектердiң қасиеттерi бойынша мына шектен
шектер бар болсын. Онда шектердiң қасиеттерi бойынша мына шектен  осыдан
осыдан  яғни 3-анықтама бойынша
яғни 3-анықтама бойынша  түзуi
түзуi  функциясының көлбеу асимптотасы.
функциясының көлбеу асимптотасы.
[pr] Мысал.  қисықтың асимптоталарын табу керек.
қисықтың асимптоталарын табу керек.
Шешiмi. 1) Қисықтың горизонталь асимптотасы жоқ, себебi 
2)  нүктесi қисықтың екiншi тектi үзiлiс нүктесi, яғни
нүктесi қисықтың екiншi тектi үзiлiс нүктесi, яғни
 Демек
Демек  нүктесi қисықтың тiк асимпто-
нүктесi қисықтың тiк асимпто-
тасы болады.
3) Ендi функцияның көлбеу асимптотасын  формулалар арқылы iздеймiз.
формулалар арқылы iздеймiз.


Сонымен  түзуi берiлген қисықтың көлбеу асимптотасы.
түзуi берiлген қисықтың көлбеу асимптотасы.
Функцияның графигiн салудың жалпы жобасы
Ендi  функциясын зерттеп графигiн тұрғызудың жолын көрсетейiк. Берiлген функцияны келесi ретпен зерттеу керек:
функциясын зерттеп графигiн тұрғызудың жолын көрсетейiк. Берiлген функцияны келесi ретпен зерттеу керек:
1) функцияның анықталу облысын табу керек;
2) функцияның координат өстерiмен қиылысу нүктелерiн табу керек;
3) функцияның тақтылығын, жұптылығын және периодтылығын анықтау керек;
4) функцияны бiрсарындылыққа және экстремумдыққа зерттеу керек;
5) функцияның дөңес, ойыс аралықтарын және иiлу нүктелерiн табу керек;
6) функцияның асимптоталарын табу керек;
7) осы мәлiметтердiң кестесiн құру керек;
8) алынған мәлiметтер арқылы функцияның графигiн тұрғызу керек.
Бақылау сұрақтары
[q][+] :1 Егер  – иілу нүктесі болса,онда
– иілу нүктесі болса,онда
[a]  [a]
[a]  [a]
[a]  [a]
[a]  [a]
[a] 
[q][+]:2  функцияның
функцияның  аралығындағы ең үлкен мәнін табу керек
аралығындағы ең үлкен мәнін табу керек
[a] 0 [a] 8 [a]16 [a] 2 [a] 1,5
[q][+] :3 Лопитальережесібойыншатабыңыз 
[a] 0 [a] 1 [a]  [a]–
[a]–  [a]
[a] 
[q][+] 2:1:Функцияныңэкстремумнүктелерінтабыныз 
[a]  [a]
[a]  [a]
[a]  [a]
[a]  [a]
[a] 
[q]1:1: Егер  болса,
болса,  функциясыбұларалықта
функциясыбұларалықта
[a]өспелі
[a]кемімелі
[a]тұрақты
[a]нөлгетең
[a]үзілістіболады
[q]1:1: Егер  болса, онда
болса, онда  функциясы бұл аралықта
функциясы бұл аралықта
[a]үзілісті
[a]кемімелі
[a]тұрақты
[a]нөлгетең
[a]өспелі
[q]1:1: Функциясының  функциясының
функциясының  нүктесінделокальдімаксимумыбарболады ,егер
нүктесінделокальдімаксимумыбарболады ,егер 
[a] 
[a] 
[a] 
[a] 
[a]дұрысжауабыжоқ
[q]1:1: Функциясының  функциясының
функциясының  нүктесінделокальдіминимумыбарболады ,егер
нүктесінделокальдіминимумыбарболады ,егер 
[a] 
[a] 
[a] 
[a] 
[a]дұрысжауапжоқ
[q]1:1: Егер  иілунүктесіболса,онда
иілунүктесіболса,онда
[a] 
[a] 
[a] 
[a] 
[a] 
[q]2:1: 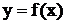 қисығына
қисығына 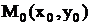 нүктесіндежүргізілгенжанаманыңтеңдеуі
нүктесіндежүргізілгенжанаманыңтеңдеуі
[a] 
[a] ] 
[a] 
[a] 
[a] 
[q]2:1:  қисығына
қисығына  нүутесіндежүргізілгеннормальдыңтеңдеуі
нүутесіндежүргізілгеннормальдыңтеңдеуі
[a] 
[a] 
[a] 
[a] 
[a] 
[q]1:1: функция  дифференциалымынағантең
дифференциалымынағантең
[a] 
[a] 
[a] 
[a] 
[a]дұрысжауапжоқ
Дата добавления: 2018-02-18; просмотров: 2779; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
