Характеристики простейших СМО
Дәріс-6 Тақырыбы: Жаппай қызмет көрсету теориясының әдістері 1. Уақиға ағындарының сипаттамалары мен мысалдары. Жаппай кызмет көрсету теориясының элементтері 2. Қарапайым ЖҚК сипаттамалары 3. Эксплуатациялық есептерді шешуге жаппай қызмет көрсету теориясын қолдану
Примеры и характеристики потоков событий. Элементы теории массового обслуживания
Примеры и характеристики потоков событий.Прежде чем изучать методы теории массового обслуживания, рассмотрим, как связаны между собой потоки событий и что они представляют собой в теории надежности.
Объектом изучения в теории эксплуатации служит техническая система. Это совокупность подсистем и элементов, нацеленных на исполнение какого-либо задания. Способность системы выполнять свои функции оценивают идеализированными понятиями о состояниях, в пределах которых выделенные параметры системы остаются неизменными. Переход системы от одного состояния к другому называют событием.
В теории надежности, например, главными состояниями принимают работоспособность и неработоспособность, а центральным понятием служит событие перехода из работоспособного в неработоспособное состояние, которое называют отказом.
Из-за большого числа элементов и множества влияющих факторов отказы в системе возникают непрерывно и образуют поток отказов, или поток событий, характеризующих реальное состояние системы.
|
|
|
В общем случае потоком событий называют последовательность однородных событий, следующих независимо друг от друга н случайные моменты времени. Примерами служат: поток отказов электрооборудования в сельскохозяйственном предприятии, поток вызовов электромонтеров на оперативное обслуживание, поток подключений к телефонной станции и т.д.
Важной характеристикой потока событий служит его интенсивность 
— среднее число событий в единицу времени. Интенсивность потока событий обычно зависит от времени. В отдельных случаях интенсивность может быть постоянной величиной.
Кроме этого, потоки оценивают по регулярности, стационарности, последствиям и т.д. Поток считают регулярным, когда события следуют, друг за другом через равные промежутки времени. Поток событий называют стационарным, если его вероятностные характеристики не зависят от времени. Когда на двух интервалах времени события не зависят друг от друга, тогда поток событий называют потоком без последствий. Поток событий считают ординарным, если появление группы (несколько) событий в небольшом интервале времени маловероятно.
По совокупности признаков выделяют простейшие, рекуррентные и др. потоки. Так, поток событий называют простейшим (пуассоновским), если он обладает сразу тремя свойствами: стационарностью, ординарностью и отсутствием последствий.
|
|
|
Элементы теории массового обслуживания.В системах с потоками событий возникает широкий круг задач, в которых ладо определить результаты применения изделий или ресурсов при случайной потребности в них. Случайный характер потоков наиболее ярко выражен при массовом применении изделий. Поэтому теорию, раскрывающую закономерности удовлетворения случайных потребностей, называют теорией массового обслуживания (ТМО). Примеры систем массового обслуживания (СМО) — различные службы сервиса, электро- и авторемонтные предприятия, билетные кассы и т. п.
Объектом изучения ТМО служит идеализированная СМО, которая состоит из следующих элементов. Источник требований (заявок) — это совокупность обслуживаемых объектов (парк электродвигателей, трансформаторов и т. д.). Накопитель — часть СМО, в которой поступившие требования находятся в очереди на обслуживание. Каналы — это приборы, исполнители и др., которые обслуживают требования ремонтом, заменой изделий или другими способами.
|
|
|
Работа СМО представляет собой случайный процесс перехода от одного состояния к другому. Если принять за исходное состояние 
— отсутствие заявки, то появление первой заявки скачком переводит СМО в состояние 
— имеется одна заявка; появление второй заявки скачком переводит СМО в состояние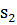 
— имеются две заявки и т.д. Аналогичные изменения происходят при окончании обслуживания, потери заявки и т.п. Такие переходы изображают размеченным графом состояний, показанным на рисунке 6.1.
При теоретическом изучении используют следующие параметры СМО: 
— количество источников заявок; 
— число каналов обслуживания; 
— интенсивность потока заявок от одного источника;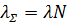 
— суммарная интенсивность потока заявок;
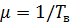— интенсивность обслуживания (ремонта) в одном канале; 
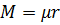— суммарная интенсивность обслуживания; 
и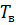 
— средние продолжительности между заявками и между завершениями обслуживания (восстановление объекта) соответственно.
Для оценки эффективности СМО применяют различные критерии. Основными из них считают: 
— среднее число занятых каналов; 
и 
— среднее число заявок в системе и в накопителе (очереди); 
и 
— средние продолжительности пребывания заявки в системе и в очереди; 
— вероятность занятости канала (загрузка канала).
|
|
|
Рис. 6.1. Граф состояний процесса «гибели и размножения»
Предмет ТМО заключается в установлении зависимости между параметра-ми СМО и ее критериями. При этом выделяют прямые задачи, когда по исходным параметрам требуется определить значения критериев, и обратные задачи, когда надо выбрать параметры СМО, обеспечивающие заданную эффективность.
Практическая значимость методов ТМО возрастает за счет дополнительного использования экономических критериев, характеризующих, во-первых, степень удовлетворения заявок источника, а во-вторых, степень использования каналов. Совместное использование этих данных позволяет найти оптимальные системы массового обслуживания.
В зависимости от состава исходных данных и решаемых задач СМО имеют разнообразные варианты. По числу каналов: одноканальные и многоканальные. По дисциплине очереди: 1 — обслуживание с отказом (если каналы свободны, то заявки обслуживаются немедленно; если каналы заняты, то заявки получают отказ и теряются); 2 — обслуживание с ожиданием в очереди по мере поступления; 3 — обслуживание с приоритетом. По размерам источника заявок: 1 — открытые — источник имеет неограниченное число заявок; 2 — закрытые — число заявок ограничено. По характеру потока заявок: простейшие и произвольные потоки.
Каждые СМО характеризуются размеченным графом (таблицей) состояний. Простейшие СМО имеют граф в виде схемы гибели и размножения, показанной на рисунке 6.1. Все состояния системы вытянуты в одну цепочку. Каждое среднее состояние (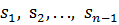 
) связано прямой и обратной стрелками со смежными состояниями, а крайние и 
— только с однимсоседним состоянием. Главная задача ТМО — определение вероятности каждого состояния СМО.
В произвольный момент времени 
система находится в состоянии 
с вероятностью 
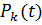. В установившемся режиме, т.е. при 
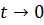произвольные вероятности состояний стремятся к своим пределам, которые называют финальными вероятностями. Для их нахождения составляют систему уравнений, характеризующих все состояния. В уравнении для каждого состояния в левой части записывают произведение финальной вероятности этого состояния на сумму интенсивностей потоков, выходящих из этого состояния, а в правой - сумму произведений интенсивностей всех потоков, входящих в данное состояние, на вероятность тех состояний, из которых потоки исходят.
В ТМО установлены аналитические связи между критериями и параметрами СМО. Например, формулы Литтла связывают продолжительность пребывания заявки в системе с числом заявок , продолжительность пребывания заявки в очереди с ее длиной :
(6.1)
}
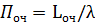Характеристики простейших СМО
Одноканальные СМО имеются в любых службах сервиса. При медицинском обслуживании это врач, принимающий пациентов, при обслуживании пассажиров — билетная касса, при техническом обслуживании энергетического оборудования — пост электрика и т. д.
Примем к рассмотрению одноканальную СМО без ограничений на длину очереди и на длительность ожидания. Пусть на эту систему поступает поток заявок с интенсивностью 
, т. е. заявки поступают в среднем через интервал времени 
. Система с интенсивностью обслуживания 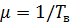обслуживает их, т. е. на каждую заявку затрачивают период времени в среднем 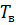. Требуется найти характеристики (критерии) работы СМО в установившемся режиме: и — среднее число заявок в системе и в накопителе (очереди); и — средние продолжительности пребывания заявки в системе и в очереди; — вероятность занятости канала (загрузка канала).
В данном случае ограничимся показательным законом распределения для и 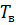, т. е. 
; 
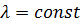. Пронумеруем возможные состояния СМО по числу заявок в ней:
- 
— канал свободен;
- 
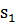— канал занят (одна заявка обслуживается, очереди нет);
- 
— канал занят (одна заявка обслуживается, одна — в очереди);
…………………………………………………………………………
- — канал занят (одна заявка обслуживается,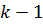 
заявка стоит в очереди).
Размеченный граф состояний показан на рисунке 6.1. Система переходит из в и далее в правом направлении под действием потока заявок с интенсивностью .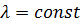
Поток восстановления (обслуживания заявок) с интенсивностью переводит систему назад — справа-налево.
Для определения финальных вероятностей, характеризующих относительную продолжительность пребывания системы в состоянии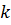 
, составим систему уравнений типа:
}
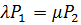……………..} (6.2)
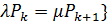
В данной задаче число состояний СМО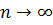 
, сумма всех вероятностей 
. Введем коэффициент нагрузки системы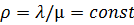 
. Он характеризует среднее число заявок, поступающих за период обслуживания одной заявки, и показывает, во сколько раз период обслуживания больше или меньше периода следования (в среднем) заявок. Обычно 
.
С учетом отмеченного, из системы (6.2) находим вероятности каждого состояния СМО
}
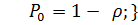
……………..} (6.3)
В установившемся режиме вероятности убывают по закону геометрической прогрессии. При любой нагрузке системы в диапазоне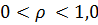 
вероятность 
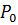больше остальных, т. е. относительная продолжительность свободного состояния системы больше продолжительности любого другого состояния.
Среднее число заявок в системе находим суммированием произведений возможных заявок 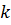на их вероятности 
:
,
где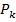 
определяем по уравнению (6.3). Окончательно получаем
(6.4)
Из полного числа заявок по (6.4) занятая обслуживанием доля пропорциональна вероятности занятости . Поскольку для СМО всегда выполняется условие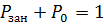 
, находим:
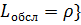(6.5)
Длину очереди определяем разностью между полным и обслуживаемым числом заявок
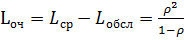(6.6)
Наконец по формулам Литтла находим средние продолжительности пребывания в системе и в очереди
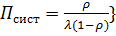(6.7)
}
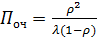Единицы измерений этих характеристик — час, сутки, год, в зависимости от единиц интенсивности поступления заявок.
Аналитическое описание характеристики одноканальной СМО иллюстрирует рисунок 6.2 для случая 
. Из графиков и формул видно, что эффективность СМО зависит от коэффициента нагрузки системы массового обслуживания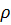 
, они существенно нелинейно. С увеличением р лишь занятость растет линейно. Другие характеристики СМО — длина очереди и продолжительность пребывания в ней — бесконечно возрастают. Таким образом, главным параметром СМО служит коэффициент нагрузки системы массового обслуживания. Для успешного функционирования системы важно выбрать правильное значение р. По характеристикам СМО ( 
, , , , и т. п.) это сделать трудно. Поэтому приходится привлекать экономические показатели как для оценки очереди заявок, так и для оценки занятости каналов. Обычно эти связи дают конкурирующие эффекты и позволяют найти оптимальные параметры СМО.
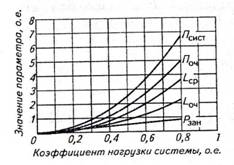
Рис. 6.2. Характеристики одноканальной СМО
Другим примером простейшей СМО служит многоканальная система с отказами. Такие системы возникли с началом развития телефонизации. Их исследование привело к созданию теории массового обслуживания, в которой рассматриваемая СМО относится к классической задаче Эрланга.
Пусть имеется 
каналов (линий связи), на которые поступает поток заявок с интенсивностью . Поток обслуживания имеет интенсивность 
. Необходимо найти характеристики системы: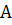 
— абсолютную пропускную способность, равную среднему числу заявок, обслуживаемых в единицу времени; 
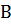— относительную пропускную способность, т. е. среднюю долю пришедших заявок, обслуживаемых системой; 
— вероятность отказа в обслуживании (канал занят);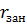 
— среднее число занятых каналов.
Графу состояний такой системы соответствует рисунок 6.1. Из состояний слева в состояние справа систему переводит поток заявок с интенсивностью , а из состояний справа-налево — поток обслуживаний с интенсивностью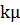 
, где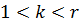 
.
Состояние системы нумеруют по числу заявок, находящихся в системе. В данном случае оно совпадает с числом занятых каналов:
- — канал свободен, в системе нет ни одной заявки;
- — в системе находится одна заявка, т.е. один канал занят, остальные каналы свободны;
………………………………………………………..
- — в системе находится 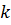заявок, т. е. 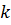каналов занято, остальные каналы свободны;
- 
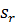— в системе находится заявок, т. е. все каналы заняты.
Если составить уравнения вероятностей для всех состояний, как в предыдущем примере, и решить полученную систему уравнений, то найдем следующие значения финальных вероятностей для нулевого 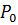и произвольного состояний
(6.8)
По ним определим искомые характеристики СМО. Относительная пропускная способность — вероятность того, что заявка будет обслужена. Она будет численно равна разности между единицей и вероятностью отказа 
, т. е. вероятностью того, что все каналы заняты:
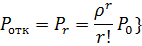
(6.9)
Абсолютную пропускную способность получим, умножая интенсивность потока заявок на вероятность их обслуживания:
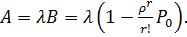(6.10)
Среднее число занятых каналов — это математическое ожидание дискретной величины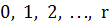 
с вероятностями этих значений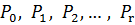 
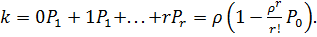(6.11)
Параметры и критерии многоканальной СМО сложным образом зависят от нагрузки системы и числа каналов. Для детального анализа следует изучать конкретные задачи.
Рассмотрим пример, который показывает, что СМО вносит существенные коррективы в традиционные представления об обслуживании электрооборудования.
Пример. Предположим, в хозяйстве имеется два дежурных электромонтера. Каждый час им поступает в среднем одна заявка на двоих на оперативное обслуживание электроустановок. Среднее время обслуживания заявки составляет один час. Итак, одна заявка поступает в течение 1 ч на двух электромонтеров. Интуитивно мы не предполагаем возможность отказа в обслуживании. Теперь проверим правильность этого предположения.
Дано: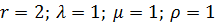 
. Определим характеристики СМО.
Решение. Финальные вероятности СМО найдем по (6.8):
Вероятность отказа определим по (6.9): 
. Среднее число занятых электромонтеров рассчитаем по (6.11):
.
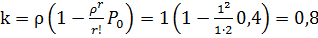Из расчета видно, что не все поступающие заявки удовлетворяются. 
заявок остаются необслуженными, хотя в среднем занят лишь один электромонтер. Таким образом, первоначальное предположение оказалось ошибочным, что подтверждает несостоятельность расчетов по средним величинам в ситуациях с нерегулируемыми потоками событий.
Дата добавления: 2018-02-18; просмотров: 1212; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!