Произведение классов Фиттинга.
Определение 55. Пусть  и
и  произвольные классы групп. Гашюцевым произведением классов
произвольные классы групп. Гашюцевым произведением классов  и
и  называется класс всех групп, являющихся расширением некоторой
называется класс всех групп, являющихся расширением некоторой  группы с помощью
группы с помощью  группы.
группы.
Обозначается:  или
или  .
.
Определение 56. Пусть  класс групп,
класс групп,  формация. Корадикальным (формационным) произведением классов групп
формация. Корадикальным (формационным) произведением классов групп  и
и  называется класс групп
называется класс групп 
Определение 57. Пусть  класс Фиттинга и
класс Фиттинга и  класс групп. Радикальным произведением
класс групп. Радикальным произведением  и
и  называется класс
называется класс  .
.
Теорема 10. Если  и
и  классы Фиттинга, то
классы Фиттинга, то  класс Фиттинга и
класс Фиттинга и  .
.
Доказательство.
Покажем, что  класс Фиттинга.
класс Фиттинга.
1) Пусть  и
и  . Покажем, что
. Покажем, что  . Поскольку
. Поскольку  , то
, то  . Из
. Из  по лемме 9 получаем:
по лемме 9 получаем:
 . Так как
. Так как  , то по теореме о соответствии получаем:
, то по теореме о соответствии получаем:
 . По условию
. По условию  ,
,  класс Фиттинга, значит,
класс Фиттинга, значит,  . Тогда
. Тогда  . Следовательно,
. Следовательно,  .
.
2) Пусть 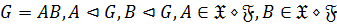 . Покажем, что
. Покажем, что  . Из
. Из  следует:
следует:  . Так как
. Так как 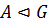 , то
, то  . Значит,
. Значит,  . Аналогичным образом получается, что
. Аналогичным образом получается, что  и
и  .
.
Рассмотрим  . Следовательно,
. Следовательно,  .
.
Из 1) и 2) получаем, что  класс Фиттинга.
класс Фиттинга.
Покажем, что  .
.
Пусть  . Покажем, что
. Покажем, что  . Так как
. Так как  , то
, то  . Следовательно,
. Следовательно,  . Значит,
. Значит,  и
и  .
.
Теорема 11. Пусть 𝔛, 𝔉 и  классы Фиттинга. Тогда
классы Фиттинга. Тогда
1)  ;
;
2)  .
.
Доказательство.
1) По теореме 10  класс Фиттинга,
класс Фиттинга,  . Значит,
. Значит,
 . Так как
. Так как  , то
, то  . Следовательно, по теореме о соответствии получим:
. Следовательно, по теореме о соответствии получим:  и
и
 .
.
Покажем обратное включение. Пусть  . Так как
. Так как  , то
, то  . Но
. Но  в силу того, что
в силу того, что  ,
,  , а значит,
, а значит,  . Из обоих включений получаем, что
. Из обоих включений получаем, что  .
.
|
|
|
Так как  , то
, то  . Следовательно,
. Следовательно,  . Поэтому
. Поэтому  . Тогда по теореме о соответствии
. Тогда по теореме о соответствии  , откуда следует, что
, откуда следует, что  .
.
Таким образом,  .
.
2) Пусть  . Тогда
. Тогда  . Значит,
. Значит,
 .
.
Следовательно,  и
и  .
.
Тогда  . Покажем обратное включение.
. Покажем обратное включение.
Пусть  . Тогда
. Тогда  . Так как
. Так как
 и по первому пункту теоремы получаем:
и по первому пункту теоремы получаем:  Значит,
Значит,  .
.
Теорема 12. Если  класс Фиттинга и
класс Фиттинга и  гомоморф, то
гомоморф, то
 .
.
Доказательство.
Из определения радикального произведения следует, что
 , то есть радикальное произведение
, то есть радикальное произведение  состоит из таких групп
состоит из таких групп  , что
, что  и
и  . Следовательно,
. Следовательно,  . Покажем обратное. Пусть
. Покажем обратное. Пусть  . Рассмотрим факторгруппу
. Рассмотрим факторгруппу  . Так как
. Так как  гомоморф, то
гомоморф, то  . Откуда следует, что
. Откуда следует, что  .
.
Глава 3. Произведение 𝛀 - расслоенных классов Фиттинга.
3.1. 𝛀 - расслоенные классы Фиттинга и их основные свойства.
Лемма 10. Пусть  группа минимального порядка из
группа минимального порядка из  , где
, где  и
и  классы Фиттинга. Следовательно,
классы Фиттинга. Следовательно,  комонолитична с комонолитом
комонолитична с комонолитом  .
.
Доказательство.
Пусть  две различные максимальные нормальные подгруппы группы
две различные максимальные нормальные подгруппы группы  из
из  . Так как
. Так как 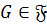 и
и  ,
,  класс Фиттинга, то
класс Фиттинга, то 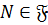 . Аналогично получается, что
. Аналогично получается, что  . Значит,
. Значит,  .
.
Так как  , то
, то  . Поскольку
. Поскольку 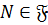 , имеем:
, имеем:  . Аналогично получается, что
. Аналогично получается, что  . Из этого можно сделать вывод о том, что
. Из этого можно сделать вывод о том, что  .
.
|
|
|
Допустим, что 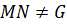 . Из
. Из  следует, что
следует, что  . А это значит, что
. А это значит, что  . Поэтому имеем:
. Поэтому имеем:  . Аналогично: из
. Аналогично: из  следует, что
следует, что  . В связи с чем получаем:
. В связи с чем получаем:  . Таким образом, имеем:
. Таким образом, имеем:  . Противоречие. Значит,
. Противоречие. Значит,  и
и  . Снова имеем противоречие. Следовательно,
. Снова имеем противоречие. Следовательно,  содержит единственную максимальную нормальную подгруппу.
содержит единственную максимальную нормальную подгруппу.
Пусть  комонолит группы
комонолит группы  . Покажем, что
. Покажем, что 
Пусть  все нормальные
все нормальные  подгруппы группы
подгруппы группы  . Из того, что
. Из того, что  максимальная нормальная подгруппа, получаем:
максимальная нормальная подгруппа, получаем:  . И из
. И из 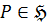 имеем:
имеем:  .
.
Допустим, что  . Тогда из
. Тогда из  получаем:
получаем:  . Противоречие. Значит,
. Противоречие. Значит,  .
.
Через  обозначают множество всех простых групп, изоморфных композиционным факторам группы
обозначают множество всех простых групп, изоморфных композиционным факторам группы  .
.
Если  , то
, то  называется
называется  -группой.
-группой.
 множество всех
множество всех  -групп.
-групп.
 .
.
Лемма 11. Пусть  и
и  – формации,
– формации,  - классы Фиттинга,
- классы Фиттинга,  – группа и
– группа и  . Тогда
. Тогда
1) если  , то
, то  ;
;
2)  ;
;
3)  ;
;
4)  , то
, то  ;
;
5)  ;
;
Определение 54. Пусть  множество всех простых групп.
множество всех простых групп.
 .
.
Функцию  , принимающую одинаковые значения на изоморфных группах из Ω, называют Ω- радикальной функцией или
, принимающую одинаковые значения на изоморфных группах из Ω, называют Ω- радикальной функцией или  -функцией.
-функцией.
Функцию  , принимающую одинаковые значения на изоморфных группах из
, принимающую одинаковые значения на изоморфных группах из  , называют радикальной функцией или -функцией.
, называют радикальной функцией или -функцией.
|
|
|
Функцию  , принимающую одинаковые значения на изоморфных группах из
, принимающую одинаковые значения на изоморфных группах из  , называют формационно-радикальной функцией или
, называют формационно-радикальной функцией или  -функцией.
-функцией.
Лемма 12. Пусть  -
-  -функция, φ -
-функция, φ -  -функция,
-функция, 
 . Тогда
. Тогда  является классом Фиттинга.
является классом Фиттинга.
Определение 58. Класс Фиттинга  назовем
назовем  -расслоенным, если
-расслоенным, если  , где
, где  - некоторые
- некоторые  -функция и
-функция и  -функция соответственно. Функцию
-функция соответственно. Функцию  будем называть
будем называть  -спутником, а функцию
-спутником, а функцию  -направлением
-направлением  -расслоенного класса Фиттинга
-расслоенного класса Фиттинга  .
.
Пусть  -
-  -функция. Класс Фиттинга
-функция. Класс Фиттинга  назовем расслоенным, а
назовем расслоенным, а  будем называть
будем называть  -спутником расслоенного класса Фиттинга
-спутником расслоенного класса Фиттинга  .
.
Лемма 13. Пусть  - класс Фиттинга и
- класс Фиттинга и  . Тогда
. Тогда
 где
где  -
-  -функция такая, что
-функция такая, что  ,
,  для всех
для всех  , и
, и  - произвольная
- произвольная  -функция. В частности, классы Фиттинга
-функция. В частности, классы Фиттинга  и (1) являются
и (1) являются  -расслоенными для любого непустого класса
-расслоенными для любого непустого класса  .
.
Доказательство.
Пусть  , где
, где  -
-  -функция такая, что
-функция такая, что  ,
,  для всех
для всех  , и
, и  - произвольная
- произвольная  -функция. Покажем, что
-функция. Покажем, что  .
.
Пусть  . Тогда
. Тогда  , и из
, и из  следует, что
следует, что  . Таким образом,
. Таким образом,  , и, значит,
, и, значит,  .
.
Предположим, что  и
и  группа наименьшего порядка из
группа наименьшего порядка из  . Тогда
. Тогда  . Следовательно,
. Следовательно, 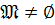 и
и  .
.
Пусть  и
и 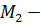 собственные нормальные подгруппы группы
собственные нормальные подгруппы группы  такие, что
такие, что  . Так как
. Так как  , то в силу выбора
, то в силу выбора  , получим, что
, получим, что
|
|
|
 , и значит,
, и значит,  . Получили противоречие. Следовательно,
. Получили противоречие. Следовательно,  комонолитическая группа с комонолитом
комонолитическая группа с комонолитом  . Тогда
. Тогда  и
и  простая группа. Если
простая группа. Если  , то
, то  , что невозможно. Поэтому
, что невозможно. Поэтому  . Тогда
. Тогда  . Противоречие. Таким образом,
. Противоречие. Таким образом,  .
.
Лемма 14. Пусть  , где
, где  произвольная
произвольная  -функция. Тогда справедливы следующие утверждения:
-функция. Тогда справедливы следующие утверждения:
1)  , где
, где  для любого
для любого  ;
;
2)  ,где
,где  и
и  для всех
для всех  ;
;
3) если  и
и  , то
, то
 .
.
Доказательство.
1) Пусть  , где
, где  -функция из пункта 1) леммы. Так
-функция из пункта 1) леммы. Так
как  для любого
для любого  , то
, то  .
.
Пусть 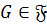 . Тогда
. Тогда  для любого
для любого
 . Поскольку класс
. Поскольку класс  является нормально наследственным, то
является нормально наследственным, то  , и значит,
, и значит,  и
и
 для любого
для любого  . Следовательно,
. Следовательно,  и
и  . Таким образом, мы получаем, что
. Таким образом, мы получаем, что  .
.
2) Пусть  -функция, описанная в пункте 2) леммы и ℌ=
-функция, описанная в пункте 2) леммы и ℌ=  . Покажем, что
. Покажем, что  . Пусть
. Пусть 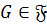 . Это означает, что
. Это означает, что  и для всех
и для всех  имеем:
имеем:  . Следовательно,
. Следовательно,  и
и  .
.
Допустим, что 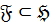 и
и  группа наименьшего порядка из
группа наименьшего порядка из  . Тогда по лемме 10 группа
. Тогда по лемме 10 группа 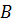 комонолитична с комонолитом
комонолитична с комонолитом  . Так как
. Так как 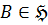 , то
, то  . Следовательно,
. Следовательно,  . Откуда получаем, что
. Откуда получаем, что  .
.
Из 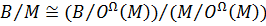 следует, что
следует, что  и
и  . Так как
. Так как  , то
, то  . Отсюда в силу нормальной наследственности класса
. Отсюда в силу нормальной наследственности класса  получаем:
получаем:  . Далее из
. Далее из 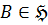 следует, что
следует, что  для любого
для любого 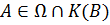 . Значит,
. Значит,  . Получили противоречие. Следовательно, допущение неверно и
. Получили противоречие. Следовательно, допущение неверно и  .
.
3) Пусть  ,
,  и
и 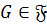 . Если
. Если  , то
, то
 по определению класса
по определению класса  .
.
Пусть  . Так как
. Так как  , то найдется такая группа
, то найдется такая группа  , что
, что  . Откуда следует, что
. Откуда следует, что  , и значит,
, и значит,  . Поскольку
. Поскольку  , то
, то  , и поэтому
, и поэтому
 .
.
Таким образом, 
 .
.
Лемма 15. Пусть  произвольная
произвольная  -функция,
-функция,  , где
, где  ,
,  . Тогда
. Тогда  , где
, где  .
.
Доказательство.
Пусть ℌ=  . Покажем, что
. Покажем, что  .
.
Пусть 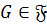 . Это означает, что
. Это означает, что  и
и  . Следовательно,
. Следовательно,  . Так как
. Так как 
 , то
, то  Значит,
Значит,  и
и  .
.
Пусть 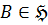 . Следовательно,
. Следовательно,  и
и
 . Отсюда получаем, что
. Отсюда получаем, что
 и
и  . Следовательно,
. Следовательно,  и
и  . Таким образом, имеем:
. Таким образом, имеем:  , и значит,
, и значит,  .
.
3.2. Произведение Ω -расслоенных классов Фиттинга.
Пусть  . Тогда
. Тогда 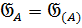 ,
,  .
.
Определение 59. Направление  Ω-расслоенного класса Фиттинга называют:
Ω-расслоенного класса Фиттинга называют:
1. 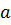 -направлением, если
-направлением, если  для любой абелевой группы
для любой абелевой группы  ;
;
2.  -направлением, если
-направлением, если  для любой абелевой группы
для любой абелевой группы  ;
;
3.  -направлением, если
-направлением, если  для некоторой простой группы
для некоторой простой группы  ;
;
4.  -направлением, если
-направлением, если  для любой неабелевой группы
для любой неабелевой группы  ;
;
5.  -направлением, если
-направлением, если  для любого
для любого  .
.
 -функцию
-функцию  называют
называют  -направлением Ω-расслоенного класса Фиттинга 𝔉, если
-направлением Ω-расслоенного класса Фиттинга 𝔉, если  является
является  -направлением для любого
-направлением для любого  .
.
Лемма 16. Пусть  простая группа и 𝔉 – непустая формация Фиттинга такая, что 𝔉
простая группа и 𝔉 – непустая формация Фиттинга такая, что 𝔉  = 𝔉. Если
= 𝔉. Если  является
является  -группой, то
-группой, то  .
.
Доказательство.
Так как 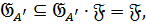 то по свойству корадикала
то по свойству корадикала  Из
Из  по теореме 9 (о соответствии) имеем:
по теореме 9 (о соответствии) имеем:  . Поскольку
. Поскольку  нормально наследственный класс групп и
нормально наследственный класс групп и  , то
, то  . Тогда, по свойству корадикала,
. Тогда, по свойству корадикала,  .
.
С другой стороны,  , а
, а  по определению 55
по определению 55  Следовательно,
Следовательно,  .
.
Таким образом,  .
.
Лемма 17. Пусть  с
с  -направлением
-направлением  . Тогда
. Тогда
1) если  и
и  , то
, то 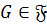 ;
;
2) если  и
и  , то
, то 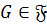 .
.
Доказательство.
1)  . Пусть
. Пусть  . По условию
. По условию  . Покажем, что
. Покажем, что
 . Так как
. Так как  , то по лемме 11 (4)
, то по лемме 11 (4)  . Тогда
. Тогда  , так как
, так как  .
.
По условию  . Пусть
. Пусть 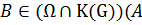 ). Покажем, что
). Покажем, что  . Из
. Из  следует, что
следует, что  .
.
По условию 
 -направление. Значит,
-направление. Значит,  . Так как
. Так как  , то
, то  и тогда по лемме 16
и тогда по лемме 16
 . Следовательно, по определению
. Следовательно, по определению  расслоенного класса Фиттинга имеем:
расслоенного класса Фиттинга имеем: 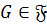 .
.
2) Из условия известно, что  . Пусть
. Пусть  ,
,  . Так как
. Так как  -группа и
-группа и  , то по лемме 16
, то по лемме 16  . Из
. Из  следует, что
следует, что  . Откуда:
. Откуда:  . Значит, по определению
. Значит, по определению  расслоенного класса Фиттинга
расслоенного класса Фиттинга 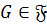 .
.
Лемма 17. Пусть 𝔐 и ℌ -  -классы Фиттинга с
-классы Фиттинга с  направлением
направлением  внутренние
внутренние  спутники классов Фиттинга 𝔐 и ℌ соответственно. Если
спутники классов Фиттинга 𝔐 и ℌ соответственно. Если  с
с  спутником
спутником  таким, что
таким, что  ,
,  для всех
для всех  и
и  для всех
для всех  , то
, то  и
и  является внутренним
является внутренним  спутником класса Фиттинга
спутником класса Фиттинга  .
.
Доказательство.
Пусть  с
с  спутником
спутником  таким, что
таким, что  ,
,  для всех
для всех  и
и  для всех
для всех
 . Покажем, что
. Покажем, что  внутренний
внутренний  спутник класса Фиттинга
спутник класса Фиттинга  .
.
Пусть  . Допустим, что
. Допустим, что  . Пусть
. Пусть  и
и  группа минимального порядка с таким свойством. Тогда по лемме 10
группа минимального порядка с таким свойством. Тогда по лемме 10  комонолитична с комонолитом
комонолитична с комонолитом  . Пусть
. Пусть  . Так как
. Так как  , то
, то 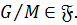 Значит,
Значит,  и
и  . Если
. Если  , то
, то  и
и  . Тогда
. Тогда  и
и  Таким образом, по лемме 17 2)
Таким образом, по лемме 17 2) 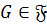 . Имеем противоречие. Поэтому
. Имеем противоречие. Поэтому  . Из того, что
. Из того, что  , следует, по определению 57 радикального произведения, что
, следует, по определению 57 радикального произведения, что  . Пусть
. Пусть  . Тогда (
. Тогда ( 
 и, значит,
и, значит,  .
.
Пусть  . Тогда
. Тогда  и
и  . В любом случае имеем:
. В любом случае имеем:  ,
, 
 . Значит, по лемме 17 1)
. Значит, по лемме 17 1) 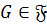 . Противоречие. Значит,
. Противоречие. Значит,  .
.
По теореме 10  . Так как
. Так как  внутренний
внутренний  спутник
спутник  , то
, то 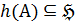 и
и  .
.
Таким образом, мы показали, что  внутренний
внутренний  спутник класса Фиттинга
спутник класса Фиттинга 
Определение 60. Класс Фиттинга  называется
называется  каноническим или, коротко,
каноническим или, коротко,  классом Фиттинга, если
классом Фиттинга, если  для любого
для любого  , и обозначается
, и обозначается  и
и 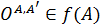 для всех
для всех  .
.
Лемма 18. Пусть  внутренние
внутренние  спутники
спутники  классов Фиттинга
классов Фиттинга  соответственно. Тогда
соответственно. Тогда  является
является  классом Фиттинга с внутренним
классом Фиттинга с внутренним  спутником
спутником  таким, что
таким, что  .
.  для всех
для всех  и
и  для всех
для всех  .
.
Доказательство.
Пусть  . Тогда по лемме 17
. Тогда по лемме 17  . Допустим, что
. Допустим, что  . Пусть
. Пусть  и группа
и группа  наименьшего порядка с таким свойством. Тогда по лемме 10
наименьшего порядка с таким свойством. Тогда по лемме 10  комонолитическая группа с комонолитом
комонолитическая группа с комонолитом  .
.
Пусть  . Тогда
. Тогда  Так как
Так как
 , то
, то  и, значит,
и, значит,  . Из
. Из  следует, что
следует, что  . Допустим, что
. Допустим, что  . Тогда
. Тогда 
 и по лемме 17 имеем:
и по лемме 17 имеем:  . Получили противоречие. Следовательно,
. Получили противоречие. Следовательно,  . Тогда
. Тогда  и, значит,
и, значит,  Из
Из  и
и  , следует, что
, следует, что  и
и  Тогда
Тогда  и
и  комонолитическая группа с комонолитом
комонолитическая группа с комонолитом  , причем
, причем  Из
Из  следует, что
следует, что  и, значит,
и, значит,  .
.
Так как  , то по лемме 17
, то по лемме 17  . Тогда
. Тогда  =
= 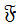 . Снова получили противоречие.
. Снова получили противоречие.
Следовательно,  .
.
Определение 61. Класс Фиттинга  называется
называется  биканоническим или, коротко,
биканоническим или, коротко,  классом Фиттинга, если
классом Фиттинга, если  для любой неабелевой группы
для любой неабелевой группы  и
и  для любой абелевой группы
для любой абелевой группы  , и обозначается
, и обозначается  и
и
 для всех
для всех  и
и 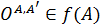 для всех
для всех  .
.
Лемма 19. Пусть  внутренние
внутренние  спутники
спутники  классов Фиттинга
классов Фиттинга  соответственно. Тогда
соответственно. Тогда  является
является  классом Фиттинга с внутренним
классом Фиттинга с внутренним  спутником
спутником  таким, что
таким, что  для всех
для всех  ,
,  для всех
для всех  и
и  для всех
для всех  .
.
Доказательство.
Пусть  .
.
Так как  для любого
для любого  , то
, то  для любого
для любого 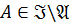 .
.
Так как  для любого
для любого  . В свою очередь, для любого
. В свою очередь, для любого 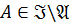
 , что показывает, что
, что показывает, что  -направление.
-направление.
По лемме 18  , где
, где  для всех
для всех
 ,
,  ,
, 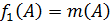 для всех
для всех  .
.
Так как  внутренний
внутренний  спутник
спутник  , то
, то  для любого
для любого  . Пусть
. Пусть  . Тогда
. Тогда  . Это означает, что
. Это означает, что
 .
.
Если 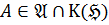 , то
, то  .
.
Если  , то
, то  .
.
Если  неабелева и
неабелева и  , то
, то  .
.
Если  неабелева и
неабелева и  , то
, то  .
.
Таким образом, 
 . Это значит, что
. Это значит, что  и
и  .
.
Допустим, что  и
и  и группа
и группа  минимального порядка с таким свойством. Тогда по лемме 10
минимального порядка с таким свойством. Тогда по лемме 10  комонолитична с комонолитом
комонолитична с комонолитом
 .
.
Пусть  . Тогда
. Тогда  и
и  . Значит,
. Значит,  .
.
Допустим, что  . Так как
. Так как  , то
, то  . Получили противоречие. Следовательно,
. Получили противоречие. Следовательно,  .
.
В случае, если  , имеем:
, имеем:  . Из
. Из  следует, что
следует, что  . Тогда
. Тогда  .
.
Так как  и
и  , то
, то  Поэтому, в свою очередь,
Поэтому, в свою очередь,  и
и  . Следовательно,
. Следовательно,  комонолитична с комонолитом
комонолитична с комонолитом  , причем
, причем  .
.
Из  следует, что
следует, что  и
и  .
.
Так как  . Тогда по лемме 17
. Тогда по лемме 17  . А это означает, что
. А это означает, что  . Противоречие.
. Противоречие.
В случае же, если  , имеем:
, имеем:  . Так как
. Так как  , то по лемме 17 получим:
, то по лемме 17 получим:  . Противоречие.
. Противоречие.
Значит, допущение неверно, и  .
.
Дата добавления: 2018-02-18; просмотров: 716; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
