Вычисление значений алгебраического многочлена (метод Горнера).

Пусть задан многочлен n -й степени

P_n(x)=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n .

Вычисление его значений при конкретном значении аргумента можно вести разными путями. Например, сначала найти все степени, затем все произведения и, наконец, выполнить все сложения - этот путь потребует, по крайней мере, 2n умножений и n сложений.

Перепишем многочлен с использованием т.н. скобок Горнера

P_n(x)=(…(((a₀)×x+a₁) ×x+a₂) ×x+…+a_n-1) ×x+a_n.

Здесь можно воспользоваться однообразным вычислительным процессом: примем за значение P коэффициент при n-й степени и затем значение P последовательно умножаем на x и добавляем следующий коэффициент. Этот путь требует лишь n умножений и n сложений, уменьшает погрешность вычислений и имеет изящную программную реализацию; например, на языке Паскаль

P := a[0] ; for k := 1 to n do P:=P*x+a[k] ;

С помощью этого метода можно переводить десятичные числа в другие системы счисления

Вычисление значений аналитических функций и степенные ряды.

При решении многих задач возникает необходимость вычисления значений некоторых функций.

Если не удастся найти готовую аппроксимацию для искомой функции, на помощь может прийти факт, что аналитическая функция может быть представлена степенным рядом: всякая аналитическая при x=x* функция F(x) разлагается в окрестности точки x* в ряд Тейлора:

(при x*=0 этот ряд называется рядом Маклорена).

Сходящиеся ряды Тейлора являются основой для вычисления значений функций в некотором диапазоне значений аргумента.

Есть ряды сходящиеся и расходящиеся. Необходимым условием сходимости ряда является стремление его n-ого члена к нулю, при n равном бесконечности. Это только необходимое условие, но не достаточное, ряд может и расходится (но если он знакочередующийся, значит точно сходится). Дальше когда необходимое условие сходимости выполнено, мы проверяем ряд на достаточное условие. Сделать можно разными способами. По признаку Даламбера, например.

Так вот, использовать разложение функции в ряд Тейлора для вычисления ее значения целесообразно применять при быстрой сходимости ряда (т.е. чем меньше членов ряда нам нужно посчитать, чтобы достигнуть определенной точности, тем лучше). В случаях, когда сходимость недостаточно быстрая, ее можно увеличить.

Метод цепных дробей.

Помимо разложения в ряд Тейлора можно еще разложить функции в виде цепной дроби.

В простой дроби нужно поделить числитель на знаменатель и выделить целую часть, а дробный остаток поделить и числитель, и знаменатель на числитель же. И так далее.

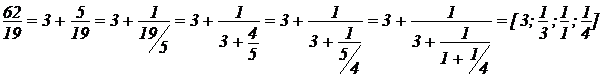
Ближе к функциям. Л.Эйлер разложил таким способом функцию e^x Посчитав это при х=1, он уже с четвертой итерации получил точность, такую какую получил бы при восьмой итерации в случае разложения в ряд Тейлора.

Итерационный метод.

М применять только для непрерывных, непрерывно дифференцируемых функций. Здесь нам нужно выбрать какое-то начальное приближение и сделать цикл с условием, в которое мы вставим погрешность абсолютную или относительную.

Чтобы найти более точную оценку нашего приближенного значения (которое мы сами выбираем) мы должны в цикле это посчитать по формуле:

Yn+1=Yn-(F(x,Yn)/F`y(x,Yn))

А в условие цикла поставим например абсолютную погрешность, т.е. Yn+1 - Yn <0.001 (можно и относительную погрешность поставить).

Вот так вот и считаем. Ну например можно такой цикл запилить:

n=1;

Y[1]=1; //начальное приближение

Y[2]=2 // это, чтобы можно было в цикл войти, т.к. матлаб не знает циклов с постусловием, потом это значение в первой же итерации перезапишется

x=10; //например х=10

while Y[n+1]-Y[n]>0.001

Y[n+1]=Y[n]-(fun(x,Y[n])/(fund(x, Y[n]);

n=n+1;

end

Плюс этого метода заключается в том, что он устойчив к промежуточным ошибкам, но нам нужно быть уверенными, что итерационный процесс сходящийся (иначе зациклиться).

3. ЧИСЛЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ.

Отделение корней.

В общем случае отделение корней уравнения f(x)=0 базируется на известной теореме, утверждающей, что если непрерывная функция f(x) на концах интервала [a,b] имеет значения разных знаков, т.е. f(a) ´ f(b)< 0 , то в указанном промежутке содержится хотя бы один корень.

Например, для уравнения f(x)= x³-6x+2=0 видим, что при x®¥ f(x)>0, при x® - ¥ f(x)<0 , что уже свидетельствует о наличии хотя бы одного корня. Если же найти точки экстремума из элементарного уравнения f’(x)= 3x²-6=0 изначения f(x) в этих точках, то легко видеть наличие трех корней (меньшего - , в интервале от - до и большего ).

Для уравнения f(x)= e^x+x=0 видим, что f(¥)>0, f(-¥)<0. Обнаружив, что f’(x)= e^x+1 ¹ 0, устанавливаем факт наличия единственного корня и остается лишь найти его.

Если предварительный анализ функции затруднителен, можно “пойти в лобовую атаку”. При уверенности в том, что все корни различны, выбираем некоторый диапазон возможного существования корней и производим “прогулку” по этому интервалу с некоторым шагом, вычисляя значения f(x) и фиксируя перемены знаков. При выборе шага приходится брать его по возможности большим для минимизации объема вычислений, но достаточно малым, чтобы не пропустить перемену знаков.

Часто на помощь приходит и графическая интерпретация задач. Так например, для упомянутого уравнения tg(x)=1/x можно построить графики двух элементарных функций y = tg(x) и y = 1/x и убедиться, что их пересечение происходит при значениях аргумента из диапазонов

[kp , (k+0.5)p ] , k = 0, ±1, ±2,...

Теперь можно выбрать интересующий нас интервал и провести уточнение корня до заданной точности.

Дата добавления: 2018-02-18; просмотров: 579; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!