Векторды базис бойынша жіктеу.

Матрицалар және оларға қолданылатын амалдар Анықтама. сандардан құралған кесте төртбұрышты матрица деп аталады және үлкен әріппен белгіленеді , мұндағы n – жол номері, m – баған номері Қысқаша матрицасы түрінде белгіленеді. Егер m=1, n>1 болса, онда матрица жол-матрица немесе жол-вектор, ал егер n=1, m>1, онда матрица – баған-матрица болады. - жол-матрица, - баған-матрица. Егер квадрат матрицаның бас диагональдан басқа элементтердің барлығы нольге тең болса, онда матрица диагональды деп аталады, яғни: Егер диагональды матрицаның барлық диагональды элементтері бірге тең болса, онда матрица бірлік матрица деп аталады және былайша белгіленеді: , бұл үшінші ретті бірлік матрица. Тікбұрышты матрицаның индексі оның өлшемін анықтайды. Бірдей өлшемді матрицаларды қосуға, санға көбейтуге болады. Матрицалардың қасиеттері. 10. Бірдей өлшемді және матрицаларының қосындысы сондай өлшемді матрица болады. Оның элементтері келесі теңдікпен анықталады: . Белгіленуі: А+В=С. 20. матрицасын k санына көбейту, әрбір элементі А матрицасының сәйкес элементтері мен k санының көбейтіндісі болатын матрица болады: . 30. Amxk матрицасын Bkxn матрицасына көбейту (яғни, бірінші көбейткіштің бағандар саны екінші көбейткіштің жолдар санына тең ) Cmxn матрицасы болады. Оның элементтері А матрицасының і-ші жолдары мен В матрицасының j-ші бағандарының көбейтіндісінің қосындысы болатын Cij элементтері, яғни: 40. Кез келген ретті квадрат матрицаны сәйкес бірлік матрицаға көбейту матрицаны өзгертпейді. Анықтауыштар, олардың қасиеттері Екіншіжәне үшінші ретті анықтауыштар. Айталық төрт саннан тұрытын квадратты кесте берілсін. Ондай кесте матрица деп аталып, былайша белгіленеді немесе , a1,b1,a2,b2 – сандары матрица элементтері. Анықтама 1.Матрицаға сәйкес екінші ретті анықтауыш деп, a1 b2 - a2 b1 санын айтады. Анықтауыш D әріпімен немесе ∆ - дельта әріпімен белгіленеді. Сонымен . Мәселен . - анықтауыштың бірінші жолының элементтері, - анықтауыштың екінші жолының элементтері, - анықтауыштың бірінші бағанының элементтері, - анықтауыштың екінші бағанының элементтері, - бас диагональ элементтері, - қосалқы диагональ элементтері. Айталық тоғыз саннан тұратын квадратты кесте (матрица) берілсін . Анықтама 2. Матрицаға сәйкес 3-ші ретті анықтауыш деп, символымен белгіленген және теңдігімен анықталған санды айтады. Мұндағы - сандары, анықтауыш элементтері; - бас диагональ элементтері, - қосалқы диагональ элементтері. Анықтауыштардың қасиеттері. Бұл қасиеттер, 2-ші реттен бастап, кез келген ретті анықтауыштарға тән. Тек үшінші ретті анықтауыштар үшін қарастырайық. 10. Егер анықтауыштың жолдары мен бағандарын ауыстырсақ, анықтауыштың мәні өзгермейді, яғни 20. Анықтауыштың екі қатарының орындарын ауыстыру анықтауышты (-1)-ге көбейткенге тең, яғни: 30. Егер анқтауыштың екі қатары бірдей болса, онда анықтауыштың мәні нольге тең, яғни: 40. Анықтауыштың қандай да бір қатарының барлық элементтерін кез келген k санына көбейту, анықтауышты осы k санына көбейткенге тең, яғни: 50. Егер анықтауыштың бір қатарының барлық элементтері нольге тең болса, онда ол анықтауыш та нольге тең. (алдыңғы қасиеттегі k=0 болғанда ). 60. Егер анықтауыштың параллель екі қатарының элементтері пропорционал болса, онда ол анықтауыштың мәні нольге тең, яғни . 70. Анықтауыштың қандай да бір қатарының әрбір элементі екі қосындыдан тұрса, онда анықтауышты екі анықтауыштың қосындысы түрінде көрсетуге болады. Олардың бірінің сәйкес қатарының элементтері бірінші қосылғыштар, ал басқасыныкі – екінші қосылғыштар. 80. Егер анықтауыштың қандай да бір қатарының элементтеріне оған сәйкес параллель қатар элементтерін кез келген ортақ k көбейткішке көбейтіп қоссақ, онда анықтауыштың шамасы өзгермейді, яғни: (70 және 60 қасиеттер негізінде). Анықтама 3.3-ші ретті анықтауыштың қандай да бір элементінің миноры деп, осы элемент орналасқан жол және баған элементтерін сызып тастағанда шыққан екінші ретті анықтауышты айтады. Мәселен, ∆ үшінші ретті анықтауыштың а1 элементінің миноры - екінші ретті анықтауыш болады, b1 элементінің миноры - және т.с.с. Анықтама 4.Анықтауыштың қандай да бір элементінің алгебралық толықтауышы деп, і –ші жол мен j –ші баған қиылысында орналасқан осы элементтің таңбасымен алынған минорын айтады. Алгебралық толықтауыш элементтің өзі сияқты үлкен әріппен белгіленеді. 90. Анықтауыштың мәні қандай да бір қатар элементтері мен олардың алгебралық толықтауыштарының көбейтінділерінің қосындысына тең, яғни келесі теңдік дұрыс: Анықтауышты осы формулалардың бірімен жазу, оны қандай да бір жол немесе баған элементтері бойынша жіктеу деп аталады. 100. Анықтауыштың қандай да бір қатарының элементтері мен оған параллель қатардың сәйкес элементтерінің алгебралық толықтауыштарының көбейтіндісінің қосындысы нольге тең, яғни: .

Кері матрица

n - ші ретті А матрицасының керіматрицасы деп және теңдіктерін қанағаттандыратын матрицасын айтады.

Анықтауышы нөлден ерекше матрицаның ғана кері матрицасы болады.

Кері марицаны табудың тәсілі.

Өлшемі n n өзгеше емес квадрат матрицанының кері матрицасы табу керек болсын. А матрицасының анықтауышын болсын:

Мысал. 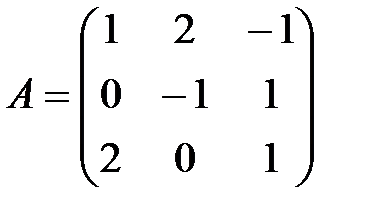матрицасына кері матрицаны табу керек.

Шешуі. Матрицаның анықтауышын есептейміз:

Матрицаның элементтерінің алгебралық толықтауыштарын есептейміз:

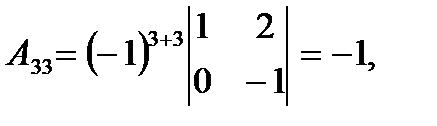
Кері матрицаны табамыз.

Матрицаның рангы. А матрицасының k-шы реттіминорыдеп матрицаның кезкелген kжолы мен кезкелген k бағандарының қиылысындағы элементтерден құрылған матрицаның анықтауышын айтамыз.

Егер матрицаның барлық k-ретті минорлары нольге тең болса, онда реті k дан үлкен болатын барлық минорлары нольге тең болады.

Матрицаның нольден ерекше минорларының ең үлкен ретін матрицаның рангысы деп аталады.

Матрицаның рангын есептеу.1.Матрицаның нольден ерекше k-шы ретті миноры таңдап алынады.

2.Таңдап алынған минорды бір жол, бір бағанмен көмкере отырып k+1-ші ретті минорды есептейміз.Ол нольге тең болса,онда берілген матрицаның рангысы k –ға тең,ал нольге тең болмаса,онда бір жол бір бағанмен көмкере отырып k+2-ші ретті минорды есептейміз.Бұл минор нольге тең болса матрицаның рангысы (k+1)-ге тең, ал нольден өзгеше болса, көмкеруден пайда болған келесі минорды есептейміз.Егер де кейінгі барлық көмкеруден шыққан минорлар нольге тең болса,онда матрицаның рангысы соңғы нольден ерекше минордың ретіне тең болады.

Мысал. матрицасының рангысын көмкеру әдісімен есептелік.

Екінші ретті М 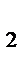минорын есептелік.

М 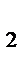= =-2+8=6 , M = 2+0-4+6-1-0=3 .

M₄= = =0.

Яғни 4-ші ретті минор нөлге тең.Нөлден ерекше минорлардың ең үлкен реті 3, сондықтан берілген матрицаның рангысы 3-ке тең.

Сызықтық теңдеулер жүйесі

n белгісізді m теңдеулерден тұратын

(1.1)

түрінде берілген жүйе сызықтық теңдеулер жүйесі деп аталады. Мұндағы х_1,х₂,...,х_n-белгісіздер, саны жүйенің i -ші теңдеуінің х_j белгісізінің алдындағы коэффициент, b - босмүшелер деп аталады.

Егер жүйедегі барлық бос мүшелер нольге тең болса, онда ол біртектіжүйе деп, ал бос мүшелердің ең бомағанда біреуі нольден өзгеше болса,онда ол біртектіемесжүйе деп аталады.

(1.1) жүйенің барлық теңдеулеріндегі х_1,х₂,...,х_nбелгісіздерінің орныны сәйкесінше λ₁, λ₂, λ₃, ..., λ_n сандарын қойғанда әрбір теңдеу тепе-теңдікке айналса, онда (λ₁, λ₂, λ₃, ..., λ_n) реттелген сандар жүйесі оның шешімі деп аталады.

Егер жүйенің шешімі бар болса,онда ол үйлесімді, ал егер шешімі жоқ болса, онда ол үйлесімсізжүйе деп аталады. Біртекті сызықтық теңдеулер жүйесі үйлесімді, өйткені (0,0,0,....0) оның шешімі болады

(1.1) жүйедегі белгісіздер алдындағы коэффициенттерден құралған mxn өлшемді А матрицасын 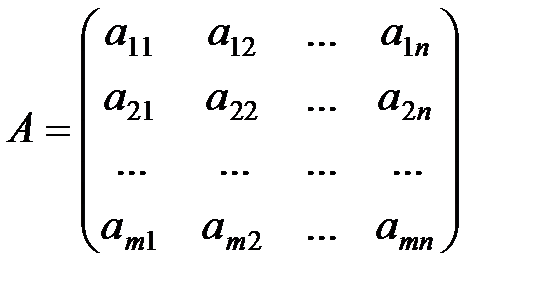жүйенің негізгі матрицасы деп, ал mx(n+1) өлшемді = матрицасы (1.1) жүйенің кеңейтілген матрицасы деп аталады.

Теорема. Сызықты теңдеулер жүйесінің үйлесімді болуы үшін жүйенің негізгі матрицасының рангысы оның кеңейтілген матрицасының рангысына 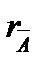тең болуы қажетті және жеткілікті, яғни = .

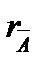Матрицаның рангысы мен белгісіздер саны тең болғанда ғана үйлесімді(1) теңдеулер жүйесінің бір ғана шешім болады.

Мысал. 4 белгісізді 3 теңдеуден тұратын біртекті емес сызықтық жүйе берілген:

Жүйенің үйлесімді болуын, не болмауын анықтау керек.

Шешуі.Кеңейтілген матрицанының рангысын есептейміз:

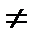r = 3. Негізгі матрицаның рангысы =2. Соныменен, r r . Сондықтан жүйе үйлесімсіз.

n белгісізді n біртекті сызықтық теңдеулер жүйесінің нөлден өзге шешімдері болуы үшін жүйенің негізгі матрицасының анықтауышы нөлге тең болуы қажетті және жеткілікті.

Үш x, y, z белгісізді үш сызықтық теңдеу жүйесін қарастырайық:

(1)

(x, y, z алдындағы коэффициенттер h₁,h₂,h₃ бос мүшелері берілген деп есептеледі).

Егер x_o, y_o, z_o үш сандар парын (1) жүйенің x, y, z айнымалыларының орнына қойғанда (1) барлық теңдеу де тепе - теңдікке айналатын болса, онда x_o, y_o, z_o - сандар пары (1) жүйенің шешуі деп аталады.

1. Жүйені Крамер әдісімен шығар.

Келесідей белгілеулер енгізейік:

∆ анықтауышы (1) жүйенің анықтауышы деп аталады. ∆_х, ∆_у, ∆_z анықтауыштары ∆ жүйенің анықтауышынан сәйкес бірінші, екінші, үшінші бағандарын бос мүше элементтерімен ауыстыру арқылы алынған. Екі жағдай қарастырайық.

1 жағдай. 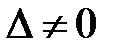. Бұл жағдайда (1)жүйенің шешуі бар және ол біреу ғана, және келесі формуламен анықталады:

(2)

(2) формулалары Крамера формулалары деп аталады.

2 жағдай. ∆=0, ∆_х=∆_у= ∆_z=0

Бұл жағдайда (1) жүйенің шексіз көп шешімі болады (шешуі болмауы да мүмкін).

Біртекті жүйені қарастырайық.

Мұндағы , яғни:

(3)

Егер 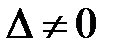болса,онда (3) жүйенің бір ғана нольдік шешімі х=0, у=0, z=0 болады.

1) Айталық ∆ анықтауыштың бір миноры нольден өзгеше болсын. Айталық, мәселен . Онда (4)

Үш белгісізді екі теңдеуден тұратын біртекті жүйе аламыз.

; ;

Онда (4) жүйенің шешімі Крамер формулалары бойынша

деп алайық; мұндағы t кез келген мән қабылдайды. Онда (4) біртекті жүйенің келесі формулалармен анықталған шексіз көп шешімі болады:

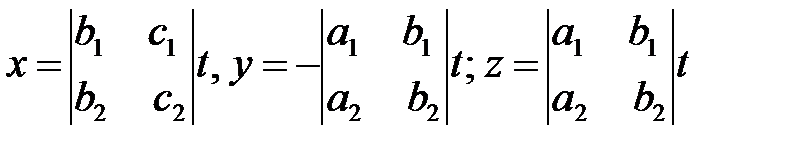(5)

2) Айталық анықтауыштың барлық минорлары нольге тең болсын. Бұл дегеніміз (3) барлық үш теңдеудің коэффициенттерінің пропорционалдығын білдіреді. Онда бір ғана теңдеу шығады және оның шексіз көп шешімі болады.

,бірақ анықтауыштың біреуінің мәні нольден өзгеше. Онда (2) формуладан алатынымыз, . Егер деп есептесек, онда теңдікте мүмкін емес жағдай аламыз. Яғни (1) жүйенің шешімі жоқ.

Векторлар, оларға қолданылатын амалдар

Анықтама 1.Бағытталған кесінді вектор деп аталалды. Вектор немесе символымен белгіленеді. А – вектордың басы, В – вектордың ұшы.

Басы мен ұшы беттесетін векторлар нольдік векторлар деп аталады және немесе жай ғана О деп белгіленеді.

Вектордың басы мен ұшы арасындағы қашықтық оның ұзындығы деп аталады және немесе деп белгіленеді.

және векторлары коллинеарлы деп аталады, егер олар бір түзу бойында немесе параллель түзулерде жатса. Коллинеарлы векторлар бағыттас немесе қарама-қарсы бағытта болуы мүмкін.

Анықтама 2. және векторлары тең деп аталады, егер олар:

1) олар коллинеарлы және бірдей бағытталған және

2) олардың ұзындықтары тең, яғни болса.

Егер және векторлары үшін және шарттары орындалса, онда олар қарама-қарсы векторлар деп аталады және теңдігі орындалады. Егер болса, онда оған қарама-қарсы вектор .

Векторлардың теңдігінің анықтамасынан, векторларды ұзындығы мен бағытын өзгертпей параллель көшіруге болатындығы шығады.

Вектордың оске проекциясы

Айталық кеңістікте қандай да бір l осі және қандай да бір векторы берілсін.

Жазықтықтың А және В нүктелері арқылы l осіне перпендикулярлар жүргіземіз. Жазықтықтардың l осімен қиылысу нүктелерін А₁ және В₁ деп белгілейміз.

векторының l осіне проекциясы деп, бағытталған кесіндісінің l осіне бағытталған А₁В₁шамасынайтады және 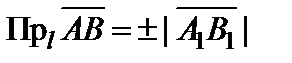деп белгілейді. (+) таңбасы векторының бағыты l осімен бағыттас болған жағдайына, ал (-) таңбасы векторының бағыты l осіне қарама-қарсы болған жағдайына сәйкес алынады.

Теорема 1. векторының l осіне проекциясы деп, векторының ұзындығы, яғни , және векторы мен l осі арасындағы бұрыштың косинусының көбейтіндісін айтады, яғни

мұндағы

Теорема 2.Тең векторлардың бір оске проекциялары тең болады.

Oxyzтік бұрышты координат жүйесін және еркін векторын қарастырайық. векторының басын О координат басына орналастырайық және оның ұшын М әрпімен белгілейік.

векторының координат остеріне проекцияларын оның координаталары деп атайды және былайша белгілейді: .

Теорема 3.А(х₁;y₁;z₁) және В(х₂;y₂;z₂) нүктелері қандай болмасын, векторының координаталары келесі формулалармен анықталады:

Х=х₂-х₁, У=у₂-у₁, Z=z₂-z₁

Егер М(x;y;z) нүктесінің координаталары болса, онда векторының координаталары

Х=х, У=у, Z=z.

Вектор ұзындығы және бағыттаушы косинустары

Егер М нүктесі арқылы координата остеріне перпендикуляр жазықтықтар жүргізсек, онда олар жазықтықтың координаталарымен бірге, диагоналі ОМ кесіндісі болатын, тік бұрышты параллелепипед құрайды. Элементар геометриядан білетініміздей, тік бұрышты параллелепиптің диагоналінің квадраты оның үш өлшемінің квадраттарының қосындысына тең. Сондықтан,

бірақ

Сонымен, алатынымыз

немесе

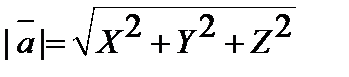Бұл формула кез келген вектордың ұзындығын оның координаталары арқылы өрнектейді.

арқылы векторы мен координата остері арасындағы бұрыштарды белгілейміз, яғни

Онда алатынымыз,

мәндері векторының бағыттаушы косинустары деп аталады. Жоғарыдағы теңдіктің әрқайсысының оң және сол жағын кватраттап нәтижелерін қосу арқылы алатынымыз

=1.

Кез келген А(х₁;y₁;z₁) және В(х₂;y₂;z₂) нүктелерін қарастырайық. Онда вектордың координаталарын анықтау формулалары бойынша .

Ұзындығы .

Векторларға сызықтық амалдар және олардың қасиеттері

Векторларға сызықтық амалдар деп,векторларды қосу және алу, векторларды санға көбейту амалдарын айтады.

1. Екі векторды қосу. Айталық және векторлары берілсін. векторы деп, векторы векторының ұшына қойылған жағдайда векторының басынан векторының ұшына жүргізілген векторды айтады.

Векторларды алу амалы қосу амалына керісінше. және векторларының айырымы деп, болатын векторын айтады.

және векторларының айырымын және - векторларының қосындысы ретінде қарастыруға болады.

2.Векторды санға көбейту. Айталық векторы және саны берілсін. көбейтіндісі деп, векторын айтады және де ол:

1) векторына коллинеар, яғни ,

2) ұзындығы

3) және бағыттас, егер , яғни және қарама-қарсы, егер , яғни .

3. Сызықтық амалдардың негізгі қасиеттері

1⁰. (қосудың ауыстырымдылық қасиеті). Суретте

Айталық векторлары берілсін. Табу керек .

2⁰. (қосудың терімділік қасиеті).

3⁰. - кез келген сандар (көбейтудің терімділік қасиеті).

4⁰. 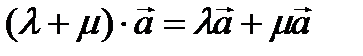(қосуға қатысты үлестірімділік қасиеті).

5⁰. (векторларды қосуға қатысты үлестірімділік қасиеті).

Векторлардың проекциялары жөніндегі келесі теоремаларды қарастырайық.

Теорема 4.Екі вектордың қосындысының оске проекциясы олардың осы оске проекцияларының қосындысына тең, яғни

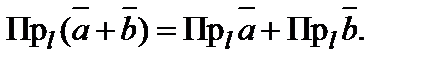
Теорема 5. векторының санына көбейтіндісінің оске проекциясы, осы вектордың оске проекциясын санына көбейткенге тең, яғни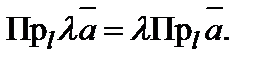

Сонымен, егер және векторлары өзінің проекцияларымен немесе координаталарымен берілсе, онда

Осылайша

Екі вектордың коллинеарлық шарты координаталарымен теңдігінен алынады.

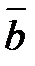яғни және векторлары коллинеарлы сонда тек сонда ғана, егер олардың координаталары пропорционал болса.

Векторды базис бойынша жіктеу.

Айталық - координат остерінің бірлік векторлары болсын, яғни және олардың әрқайсысы сәйкес координата остерімен бірдей бағытта болсын. векторлар үштігін базис деп атайды.

Теорема 6.Кез келген векторы бір ғана жолмен базисі арқылы жіктеледі, яғни түрінде көрсетіледі, мұндағы X,Y,Z - векторының координата остеріне проекциялары немесе оның координаталары.

Векторларды қосу анықтамасы бойынша алатынымыз:

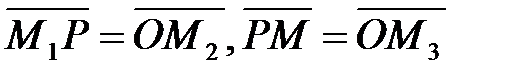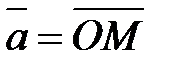болғандықтан, векторлары векторының координата остері бойынша құраушылары болады.

онда және т.б.

Векторларға сызықтық емес амалдар

Векторларға сызықтық емес амалдарға жататындар. Екі вектордың скаляр көбейтіндісі, екі вектордың векторлық көбейтіндісі, үш вектордың аралас көбейтіндісі.

1. Екі вектордың скаляр көбейтіндісі және олардың қасиеттері

Анықтама.Екі нольдік емес және 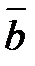векторларының скаляр көбейтіндісі деп, бұл векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусының көбейтіндісінен шыққан санды (скалярды) айтады.

Скаляр көбейтінді немесе деп белгіленеді.

Онда анықтама бойынша , мұндағы - және 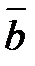векторлары арасындағы бұрыш.

болғандықтан, деп жазуға болады.

Скаляр көбейтіндінің қасиеттері.

1⁰. (көбейтіндінің орын ауыстырымдылық заңы).

2⁰. (скаляр көбейтіндіге қатысты қиюласу заңы)

3⁰. 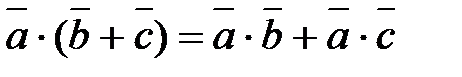(векторлар қосындысының үлестірімділік заңы).

4⁰. , яғни вектордың скаляр квадраты осы вектордың ұзындығының квадратына тең. Осыдан векторының ұзындығы былайша анықталады:

5⁰. , егер (векторлардың ортогональдылық шарты)

6⁰. Егер 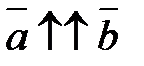, онда , ал егер , онда

4⁰ және 5⁰ қасиеттерден базистік векторлары үшін келесі теңдік алынады:

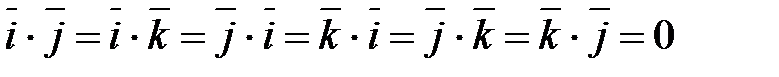және .

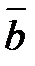Егер және векторлары өз координаталарымен берілсе: онда олардың скаляр көбейтіндісі келесі формуламен анықталады:

және 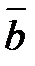векторлары арасындағы бұрышты табу формуласы:

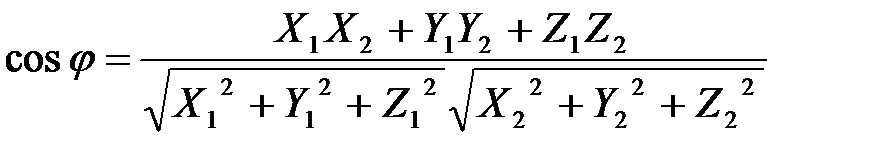теңдігінен, шығатыны .

Векторлық және аралас көбейтінділер.

Векторлардың векторлық көбейтіндісі

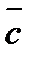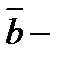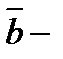Үш компланар емес векторлары берілсін. Егер векторының ұшынан қарағанда дан ға дейінгі ең қысқа бұрылыс сағат тіліне қарсы бағытта орындалса, онда векторлары оң үштік, ал дан ға дейінгі ең қысқа бұрылыс сағат тілімен бағыттас болса, онда сол үштік құрайды дейді.

Анықтама. және векторларының векторлық көбейтіндісі деп, келесі үш шартты қанағаттандыратын векторын айтады:

1) ;

2) 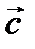векторының ұзындығы 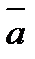және векторларына тұрғызылған параллелограммның ауданына тең, яғни , мұндағы ;

3) векторлары оң үштік құрайды.

Векторлық көбейтінді немесе деп белгіленеді.

Векторлық көбейтіндінің анықтамасынан , , болады

Векторлық көбейтіндінің қасиеттері:

1. ;

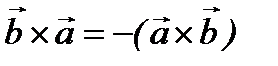2. ;

3. Нөлдік емес және векторлары жағдайда ғана колинеар;

4. .

Теорема. Егер базисінде векторлары берілсе, онда .

1-мысал. векторларының векторлық көбейтіндісін табу керек.

Векторлық көбейтіндінің қолданылуы

1. ,

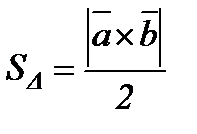
2. Егер || болса, онда (және керісінше)

Векторлардың аралас көбейтіндісі

Анықтама. , , векторларының аралас көбейтіндісі деп, және векторларының векторлық көбейтіндісі мен векторының скаляр көбейтіндісін айтады.

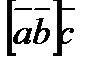Аралас көбейтінді не немесе түрінде жазылады. Аралас көбейтіндінің нәтижесі санға тең.

Аралас көбейтіндінің қасиеттері:

1. ;

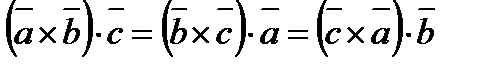2. ;

3. ;

4. Егер векторлар , , компланар болса, онда .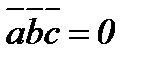

Теорема. базисінде , , векторлары берілсін, онда олардың аралас көбейтіндіні анықтауыш түрінде жазуға болады.

Аралас көбейтіндінің қолданылуы

Егер болса, онда , , -оң үштік; егер 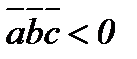болса, онда , , - сол үштік құрайды.
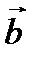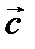, , векторлары компланар.
, .

Түзудегі және жазықтықтағы нүктенің координаталары.

Кесіндіні берілген қатынаста бөлу

Аналитикалық геометрия - геометриялық фигураларды алгебралық әдістермен қарастыратын математиканың бір бөлімі. Француз математигі Рене Декарт аналитикалық геометрияның аппараты болатын координат жүйесін құрды.

Координат жүйесі негізіне координата осі, координат жүйесі ұғымдары кіреді. Тік бұрышты (декарт) және поляр координат жүйесін қарастырайық.

Егер түзуде оң бағыт көрсетілсе, оны координат осі деп атайды, ал О нүктесі – санақ басы немесе координат басы деп аталады.

Горизонталь осінің оң бағыты деп солдан оңға қарай бағытты, ал вертикаль ось үшін төменнен жоғары қарай бағыт алынады.

Ортақ О координат басы және бірдей масштабты бірлігі бар, екі перпендикуляр ось, тік бұрышты (декарт) координат жүйесін құрайды.

Горизонталь ось - Ох осі немесе абсцисса осі, вертикаль ось – Оу осі немесе ордината осі деп аталады. Олар – координат остері. О остердің қиылысу нүктесі - координат басы. Ох және Оу остері орналасқан жазықтық - координата жазықтығы деп аталып, Оху деп белгіленеді.

Егер остің екі нүктесімен шектелген кесіндісінің басы және ұшы қайсысы екендігі көрсетілсе, онда ол бағытталған деп аталады. Бағытталған кесіндісі латын алфавитінің екі бас әрпімен белгіленіп, бірінші әрпі - басы, ал екінші әрпі – ұшы деп аталып, жоғары жағынан ортақ стрелка қойылады, .

Бағытталған кесіндінің бағыты ось бағытымен сәйкес келсе оның ұзындығы плюс таңбасымен алынады, егер олардың бағыттары қарама-қарсы болса, онда минус таңтасымен анықталады. бағытталған кесіндінің ұзындығын 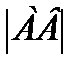деп белгілейміз

А В

Айталық М – жазықтықтың кез келген нүктесі болсын. Ол нүктеден Ох және Оу остеріне перпендикулярлар түсірейік.

М нүктесінің тік бұрышты координаталары х және у деп, сәйкес ОМ_х және ОМ_у.шамаларын айтамыз. М нүктесінің х-абсциссасы, у-ординатасы және жазылуы М(х;y). Координат басының координаталары (0;0).

Екі нүктенің ара қашықтығы.Жазықтықтағыкез келген А(х₁; у₁) және В(х₂; у₂) нүктелерінің d ара қашықтығы келесі формуламен анықталады:

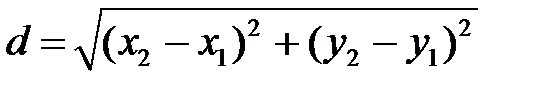(1)

Кесіндіні берілген қатынаста бөлу. Егер С(х; y) нүктесі АВ кесіндісін

(2)

қатынаста бөлсе, онда бұл нүктенің координаталары мынадай формуламен табылады:

мұндағы (х₁;у₁) – А нүктесінің координаталары, (х₂;у₂) - B нүктесінің координаталары.

Салдар: Егер С(х;у) нүктесі АВ кесіндісінің ортасы болса, онда 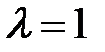және (3) формуладаналатынымыз:

(4)

Үшбұрыштың ауданы.

Бір түзу бойында жатпайтын А(х₁;у₁), В(х₂;у₂) және С(х₃, у₃) нүктелері үшін, АВС үшбұрышының S ауданы төменгі формуламен өрнектеледі:

(+) - квадрат жақшадағы оң санға, (-) – теріс санғасәйкес.

Поляр координат жүйесі - полюс деп аталатын қандай да бір О нүктесінен, одан шығатын ОЕ-поляр осінен және кесінді ұзындығын өлшеу үшін масштаб бірлігінен тұрады.

Айталық поляр координат жүйесі және жазықтықтың кезкелген М нүктесі берілсін. - М мен О нүктелерінің ара қашықтығы, яғни - бұрыш, ОЕ поляр осін ОМ сәулесімен беттесетіндей етіп бұру бұрышы.

және сандары поляр координаталары деп аталады. - бірінші координата, поляр радиусы, ал - екінші координата, полярлық бұрыш. Онда нүкте

Жазықтықтың М нүктесінің поляр және тік бұрышты координаталары арасындағы байланыс келесі формулалармен өрнектеледі:

(6)

(6) формулалар тік бұрышты координаталарды поляр координаталарымен өрнектейді:

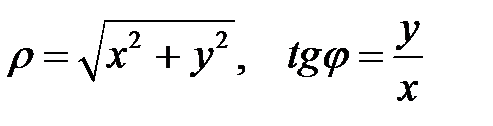(7)

(7) формулалар поляр координаталарын тік бұрышты координаталармен өрнектейді.

Ескерту. полярлық бұрыштың екі мәнін анықтайды, себебі . Екі мәннен (6) теңдік қанағаттанатын мәнін таңдап алады.

Жазықтықтағы түзу

1. Бұрыштық коэффициентті түзудің теңдеуі

Айталық қандай да бір түзу берілсін. Түзудің Ох осіне еңкею бұрышы деп, Ох осін бұрғанда, оның оң бағыты түзудің бір бағытымен беттесетіндей етіп бұру бұрышын айтады. Көбінесе Ох осін сағат тіліне қарсы бағытта бұру керек. Онда еңкею бұрышының тангенсі түзудің бұрыштық коэффициенті деп аталып k әрпімен белгіленеді:

Егер түзудің бұрыштық коэффициенті k болып ол Оу осінен шамасы в болатын ОВ кесіндісін қиса, онда оның теңдеуінің түрі

. (2)

(2) теңдеу бұрыштық коэффициенті k болатын түзудің теңдеуі деп аталады.

Егер k=0 болса, онда у=b (2₁) түзуі Ох осіне параллель болады.

Егер b=0 болса, онда y=kx (2₂) – түзуі О(0;0) координат басы арқылы өтеді.

2. Бұрыштық коэффициенті беріліп және берілген нүкте арқылы өтетін түзудің теңдеуі

Түзудің M₁(x₁;y₁) нүктесі және k бұрыштық коэффициенті белгілі болса, түзудің теңдеуін табу керек болсын.

y=kx+b теңдеуін жазайық, мұндағы в-белгісіз сан. Түзу M₁ нүктесі арқылы өтетін болғандықтан, y₁=kx₁+b теңдігі орындалады. Осыдан b=y₁-kx₁

Мұны (2) теңдеуге қойып, түзудің ізделінді теңдеуін аламыз.

y-y₁=k(x-x₁) (3)

3. Берілген екі нүкте арқылы өтетін түзудің теңдеуі

Айталық M₁(x₁;y₁) және M₂(x₂;y₂) нүктелері берілсін. (3) түрдегі түзудің теңдеуін жазайық, мұндағы k - әлі белгісіз бұрыштық коэффициент.

y-y₁=k(x-x₁).

M₂(x₂;y₂) нүктесінің координаталары да осы теңдеуді қанағаттандырады, себебі M₁M₂ түзуі M₂ нүктесі арқылы өтеді: y₂-y₁=k(x₂-x₁).

Бұл теңдіктен k – ны тауып ( шарты орындалғанда), оны (3) теңдікке қою арқылы, түзудің ізделінді теңдеуін аламыз:

(3₁)

Егер болса, оны мынадай түрде жаза аламыз.

(4)

Егер y₁=y₂болса, онда түзудің ізделінді теңдеуі: y=y₁. Бұл жағдайда түзу Ох осіне параллель. Егер x₁=x₂болса, онда түзу Оу осіне параллель және оның теңдеуі: x=x₁.

4. Екі түзу арасындағы бұрыш

L₁ және L₂ екі түзу қарастырайық.

Айталық L₁ – түзуінің теңдеүі y=k₁x+b₁болсын, мұндағы , ал L₂ - түзуінің теңдеуі y=k₂x+b₂, мұндағы . - деп L₁ және L₂ түзулері арасындағы бұрышты белгілейік: .

және арасындағы тәуелділік былайша анықталады: немесе ,

Осыдан немесе 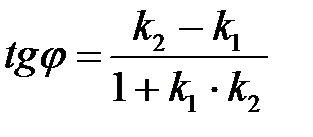(5)

(5) формула түзулер арасындағы бір бұрышты анықтайды. Ал екіншісі .

5. Екі түзудің параллельдік және перпендикулярлық шарты

Егер L₁ және L₂ түзулері параллель болса, онда және . Бұл жағдайда (5) формуланың оң жағының алымы нольге тең: k₂-k₁=0, бұдан

k₂=k₁

Егер L₁және L₂ перпендикулярлы болса, яғни 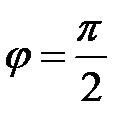, онда

Екі түзудің перпендикулярлық белгісі, олардың бұрыштық коэффициенттері шамалары жағынан кері және таңбасы қарама - қарсы.

6. Түзудің жалпы теңдеуі

Теорема.Түзу тік бұрышты координат жүйесінде кез келген х және у айнымалыларының бірінші дәрежелі теңдеуімен анықталады

Ах+Ву+С=0 (6)

Егер (6) теңдеудің қандайда бір коэффициенті нульге тең болса, онда ол толық емес теңдеу деп аталады.

Жазықтықтың теңдеуі

Жазықтық бірінші ретті бетке жатады.

1. Жазықтықтың жалпы теңдеуі. Оxyz тік бұрышты координат жүйесінде Q жазықтық пен нүктесін және Q жазықтыққа перпендикуляр векторын қарастырайық. M(x;y;z) нүктесі – жазықтықтың кез келген нүктесі.

векторы векторына перпендикуляр. Онда скаляр көбейтіндісі координаталық түрде

А(х-х₀)+В(у-у₀)+С(z-z₀)=0. (1)

(1) теңдеу берілген нүкте арқалы өтетін жазықтықтың теңдеуі. Q жазықтығына перпендикуляр жазықтықтың векторы жазықтықтың нормаль векторы деп аталады. (1) –дегі жақшаны ашып, Д=-Ax₀-By₀-Cz₀ белгілеуін енгізу арқылы, алатын теңдеуіміз

Ах+Ву+Cz+Д=0 (2)

Бұл жазықтықтың жалпы теңдеуі деп аталады. Мұндағы (яғни, А,В,С коэффициенттерінің ең болмағанда біреуі нольден өзгеше).

(2) түрдегі жазықтықтың жалпы теңдеуінің дербес жағдайларын қарастырайық.

1 - жағдай. Д=0 болса, Ах+Ву+Cz=0 жазықтығы, О(0; 0; 0) координат басы арқылы өтеді.

2 - жағдай. Егер жазықтықтың теңдеуінде х немесе у, немесе z координаттары бар мүше болмаса, онда жазықтық Ох немесе Оу, немесе Oz сәйкес остеріне параллель болады. Мәселен, айталық А=0 болса, онда By+Cz+Д=0 теңдеуі - Ох осіне параллель жазықтықты анықтайды.

3 - жағдай. Егер С=Д=0, онда Ах+Ву=0 теңдеуі Oz осі арқылы өтетін жазықтықты анықтайды. Осыған ұқсас, By+Cz=0 және Ax+Cz=0 теңдеулері Ох және Оу сәйкес остері арқылы өтетін жазықтықтарды анықтайды.

4 - жағдай. А=В=0 болса, онда Сz+Д=0 теңдеуі Оху координат жазықтығына параллель жазықтықты анықтайды. Осыған ұқсас, Ах+Д=0 және Ву+Д=0 теңдеуі, сәйкес Оуz және Охz координат жазықтығына параллель жазықтықты анықтайды.

5 - жағдай. Егер А=В=Д=0 болса, теңдеу түрі Cz=0, немесе z=0 - Оху координат жазықтығы. у=0 - Oxz координат жазықтығы, ал х=0 - Оуz координат жазықтығы.

2. А₁х+В₁у+С₁z+Д₁=0 және А₂х+В₂у+С₂z+Д₂=0 сәйкес теңдеулерімен берілген Q₁және Q₂ жазықтықтарының арасындағы бұрыш, олардың және нормаль векторлары арасындағы бұрышқа тең және келесі формуламен анықталады:

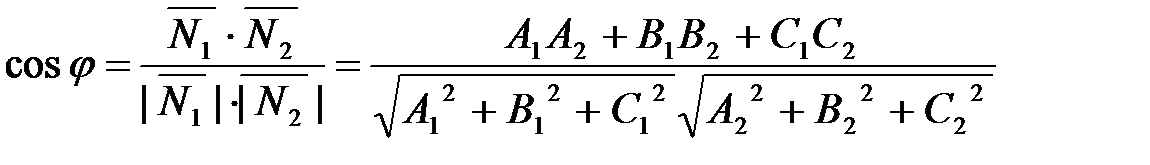3. Егер Q₁және Q₂ жазықтықтары параллель болса, онда олардың және нормаль векторлары коллинеарлы болады және керісінше. Онда

Бұл шарт Q₁және Q₂ жазықтықтарының параллельдік белгісі болады.

4. Егер Q₁және Q₂ жазықтықтары перпендикуляр болса, онда олардың және нормаль векторлары да перпендикулярлы болады, және керісінше.

Онда (векторлардың скаляр көбейтіндісі нульге тең), координаталық түрде А₁А₂+В₁В₂+С₁С₂=0 - екі жазықтықтың перпендикулярлық белгісі.

5. М₁(x₁;y₁;z₁) нүктесінен Ax+By+Cz+Д=0 жазықтығына дейінгі қашықтықты табу формуласы(жазықтықтағы нүктеден түзуге дейінгі қашықтықты табу формуласына ұқсас)

Кеңістіктегі түзудің теңдеуі

Кеңістіктегі түзу параллель емес екі жазықтықтың қиылысуы ретінде анықталады және мынадай теңдеумен беріледі:

Бұл теңдеу кеңістіктегі түзудің жалпы теңдеуі.

1. Кеңістіктегі түзудің канондық теңдеуі

Айталық кеңістіктеl түзуі және оған параллель векторы берілсін, (вектор түзу бойында да жатуы мүмкін).

векторы түзудің бағыттаушы векторы деп аталады .

М₀ – түзудің берілген нүктесі, ал М – кез келген нүкте. М₀(x₀;y₀;z₀), M(x;y;z). векторы векторына коллинеарлы. Онда векторлардың коллинеарлық белгісінен алатынымыз,

Бұл теңдеуді l түзуінің канондық теңдеуі деп айтады.

2. Түзудің параметрлік теңдеуі

Айталық l түзуі канондық теңдеумен берілсін. t арқылы әр қатынасты белгілейік. Онда

осыдан

x=x₀+mt, y₌y₀+nt, z=z₀+pt .

Алынған теңдеу l түзуінің параметрлік теңдеуі деп аталады.

3. Түзулер арасындағы бұрыш. Түзулердің параллельдік, перпендикулярлық белгілері

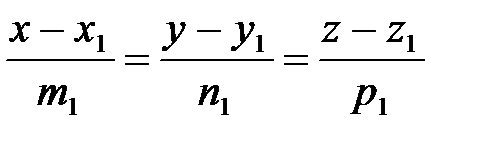және 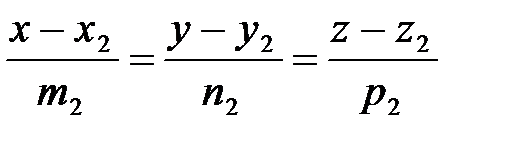сәйкес теңдеулерімен берілген l₁ және l₂түзулерінің арасындағы бұрыш деп, және , мұндағы және бағыттаушы векторлар, арасындағы бұрышты айтады және келесі формуламен анықтайды:

Егер l₁ және l₂ түзулері параллель болса, онда олардың және , бағыттаушы векторлары да параллель (яғни коллинеарлы) болады

Теңдік түзулердің параллельдік белгісі.

Егер l₁ және l₂ түзулері перпендикулярлы болса, онда олардың және , бағыттаушы векторлары да перпендикулярлы болады, яғни , онда координаттық түрде

m₁m₂+n₁n₂+p₁p₂=0.

Екінші ретті қисықтар

Екінші ретті қисықтарға шеңбер, эллипс, гипербола және парабола жатады.

1.Шеңбер

Анықтама.Шеңбер деп, центрі деп аталатын М₁(х₀,у₀) нүктесінен бірдей қашықтықтағы жазықтықтың нүктелер жиынын айтады.

Егер М₁(х_0;у₀) – шеңбер центрі және М(х;у)шеңбердің кез келген нүктесі болса, онда анықтама бойынша |M₁M|=R.

Теңдіктің сол жағына екі нүкте ара қашықтығының формуласын қолдансақ , екі бөлігін квадраттап алатын теңдігіміз

(х-х₁)²+(у-у₁)²=R².

Бұл центрі М₁(х_1;у₁) нүктесінде және радиусы R болатын шеңбердің теңдеуі.

Егер шеңбердің центрі координат басымен сәйкес келсе, онда х₁=0, у₁=0. Шеңбердің теңдеуі

х²+у²=R².

Эллипс

Анықтама.Эллипс деп, фокустары деп аталатын екі нүктеге дейінгі қашықтықтарының қосындысы тұрақты шама және фокустар аралығынан үлкен болатын, жазықтықтағы нүктелердің геометриялық орнын айтады.

мұндағы b²=а²-с².

Бұл теңдеу эллипстің канондық теңдеуі деп аталады, мұндағы а эллипстің үлкен жарты осі, b - эллипстің кіші жарты осі.

Анықтама.Эллипстің эксцентриситеті деп, с/а қатынасынан шыққан санды айтады, мұндағы с – фокустар аралығының жартысы, а – эллипстің үлкен жарты осі.

Эксцентриситеті әрпімен белгіленеді

<1, себебі c<a.

r₁және r₂фокальды радиус-векторлары былайша анықталады:

3. Гипербола

Анықтама. Гипербола деп, фокустары деп аталатын берілген екі нүктеге дейінгі қашықтықтарының айырымының абсолют шамасы тұрақты және фокус аралығынан кем болатын жазықтықтағы нүктелердің геометриялық орнын айтады.

мұнда с²-а²=b².

Бұл теңдеуді гиперболаның канондық теңдеуі деп айтады.

|OA₁|=|OA₂|=a кесінділері гиперболаның нақты жарты остері деп аталады, ал |A₁A₂|=2a - нақты ось. |OB₁|=|OB₂|=в – жорымал жарты ось, ал |В₁В₂|=2в – жорымал ось. 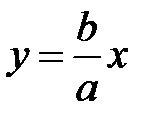және түзулері гиперболаның асимптоталары.

Анықтама.Гиперболаның эксцентриситеті деп қатынасына тең санды айтады, мұндағы с – фокустар аралығының жартысы, а – гиперболаның нақты жарты осі, яғни

мұндағы шарт бойыншаc>a.

А₁ және А₂ гиперболаның төбелері, яғни |F₁M|>|F₂M|, онда фокальдық радиустар келесі формуламен анықталады:

Кез келген тармақ үшін бұл формулалардың түрі:

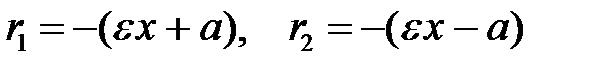
Парабола

Анықтама.Фокусы деп аталатын берілген нүктеден және директрисса деп аталатын түзуден бірдей қашықтықа жататын нүктелер жиынын парабола деп атайды.

Бұл теңдік параболаның канондық теңдеуі деп аталады.

М(х;у) нүктесінің r фокальдық радиусын

формуласыментабуғаболады.

Комплекс сандар

Кез келген комплекс санды түрінде жазуға болатындығы алгебра курсынан белгілі, мұндағы және – кез келген нақты сандар, ал -жорамал бірлік. .

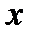саны комплекс санның нақты бөлігі деп аталып арқылы белгіленеді, 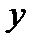жорамал бөлігі деп аталып – арқылы белгіленеді.

және комплекс сандары тең деп аталады сол жағдайда, тек қана сол жағдайда егер 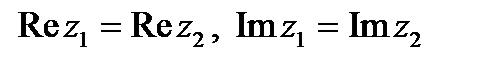болса.

және комплекс сандарының қосындысы деп комплекс санын атайды.

және комплекс сандарының көбейтіндісі деп комплекс санын атайды.

Сонымен, комплекс сандарын қосу мен көбейту, символна қатысты көпмүшеліктерге амалдар қолданғандағыдай.

саны санына түйіндес сан деп аталады.

Комплекс сандарды қосу мен көбейту амалдары коммутативтік, ассоциативтік және дистрибутивтік заңдарға бағынатынына көз жеткізу қиын емес, яғни

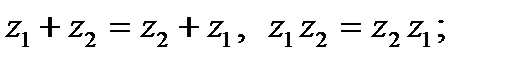
, болсын. шамасы комплекс санның модулі деп аталып, символымен белгіленеді. теңдіктерін қанағаттандыратын кез келген саны, комплекс санның аргументі деп аталып, символымен белгіленеді. шамасы тек қана нөлден өзге комплекс сандар үшін анықталады. -тің кез келген екі мәнінің айрымы -ге еселі болады.

Кез кеген комплекс санын тригонометриялық түрдеөрнектеуге болады, мұндағы .

- комплекс санның көрсеткіштік түрде жазылуы.

Кез келген натурал үшін дәрежесі Муаврформуласы арқылы өрнектеледі.

комплекс санның ші дәрежелі түбірі, әртүрлі мәнге иеболады. Олар келесі формула арқылы анықталады:

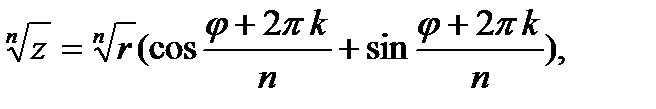
Көп жағдайда комплекс санды жазықтықтағы нүктелер бейнелеген ыңғайлы (немесе векторлармен). Әрбір , , , комплекс саннына абсцисасы 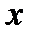және ординатасы

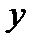болатын нүктесі немесе ОМ векторы сәйкес келтіріледі. Векторларды қосу сәйкес комплекс сандарды қосуды білдірелі.

Комплекс сандар бейнеленген жазықтық комплекс жазықтық деп, Х– осі нақты ось, ал У –жорамал ось деп аталады.

Ақырлы комплекс жазықтық Сарқылы белгіленеді.

нүктесімен толықтырылған комплекс жазықтық, кеңейтілгенкомплекс жазықтық деп , ал ол проекцияланатын сфера –Риман сферасы деп аталады.

Кеңейтілген комплекс жазықтық символымен белгіленеді.

Дата добавления: 2018-02-18; просмотров: 2600; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!