Нелинейные эффекты в процессе взаимодействия плоской электромагнитной волны с электроном.
Точные уравнения квантовой электродинамики можно записать в представлении Шредингера [213] (используется калибровка Лоренца)
 ,
, 
 (3.57)
(3.57)

где  - вектор состояния электрон-позитронного поля и поля излучения,
- вектор состояния электрон-позитронного поля и поля излучения,  - гамильтониан свободного электрон-позитронного поля,
- гамильтониан свободного электрон-позитронного поля,  - гамильтониан свободного фотонного поля,
- гамильтониан свободного фотонного поля,  - гамильтониан взаимодействия этих полей,
- гамильтониан взаимодействия этих полей,  - оператор тока электрон-позитронного тока,
- оператор тока электрон-позитронного тока,  - оператор потенциала электромагнитного поля в представлении Шредингера. До сих пор неизвестно точного решения уравнения (3.57) даже для простейших задач. Вследствие этого становится необходимым переход к модельному описанию взаимодействия фотонов и электронов.
- оператор потенциала электромагнитного поля в представлении Шредингера. До сих пор неизвестно точного решения уравнения (3.57) даже для простейших задач. Вследствие этого становится необходимым переход к модельному описанию взаимодействия фотонов и электронов.
Оператор  пропорционален е, поэтому его можно рассматривать как малое возмущение, и решение уравнения (3.57), согласно теории возмущений, можно искать в виде степенного ряда по постоянной тонкой структуры
пропорционален е, поэтому его можно рассматривать как малое возмущение, и решение уравнения (3.57), согласно теории возмущений, можно искать в виде степенного ряда по постоянной тонкой структуры  , полагая в качестве нулевого приближения
, полагая в качестве нулевого приближения  . На этом основана наиболее распространенная модель - невзаимодействующих полей, при помощи которой рассчитаны основные эффекты квантовой электродинамики [188], однако можно привести пример таких решений невозмущенной задачи, поправки к которым в любом порядке теории возмущений будут малыми. Это относится к случаю, когда внешнее поле является интенсивным и должно быть учтено точно во всех порядках теории возмущений. Таким образом, при больших плотностях фотонов [214] теория возмущений становится не корректной в рамках модели не взаимодействующих полей.
. На этом основана наиболее распространенная модель - невзаимодействующих полей, при помощи которой рассчитаны основные эффекты квантовой электродинамики [188], однако можно привести пример таких решений невозмущенной задачи, поправки к которым в любом порядке теории возмущений будут малыми. Это относится к случаю, когда внешнее поле является интенсивным и должно быть учтено точно во всех порядках теории возмущений. Таким образом, при больших плотностях фотонов [214] теория возмущений становится не корректной в рамках модели не взаимодействующих полей.
|
|
|
Существует несколько подходов к решению задачи о точном учете интенсивного электромагнитного поля в квантовой электродинамике. Достаточно указать на модель квантовой электродинамики с внешним полем [215], в которой рассматривается свободное вторично квантованное электрон-позитронное поле, возмущенное внешним электромагнитным полем, а также модели квантовой электродинамики электрона в квантованном поле излучения - модель Ван-Кампена [216] и модель Блоха-Нордсика [217].
Весьма близкой к последним двум моделям по своим исходным уравнениям и предположениям является модель электрона в плоской электромагнитной квантованной волне.
Еще в 1935 году Волковым было получено точное решение уравнения Дирака для поля плоской классической электромагнитной волны [42], электрон при этом описывался квантовомеханически. В 1969 году в работе Берсона [218] впервые было показано, что уравнение Дирака, в котором потенциал внешнего электромагнитного поля заменен оператором-потенциалом внешнего поля, решается точно, там же получена связь этих решений с решениями Волкова [42]. Вслед за [218] появилось множество работ [219-231] посвященных систематическому изучению модели электрон плюс вторично квантованная плоская волна.
|
|
|
В данной модели оказывается возможным изучить некоторые нелинейные эффекты квантовой электродинамики, к которым относятся эффекты слияния и расщепления фотонов на электроне, рассмотренные ниже. Предварительно отметим, что излучение электрона в низшем порядке теории возмущений соответствует комптон-эффекту. При этом дифференциальное сечение Клейна-Нишины [180, 181] для комптоновского рассеяния не описывает процесс излучения в поле интенсивной волны [187]. Процессами более высокого порядка являются процессы слияния и расщепления фотонов на электроне.
Впервые процесс слияния фотонов на электроне
 (3.58)
(3.58)
рассмотрел Фрид в работе [232]. В работах [233-235] изучалось слияние фотонов в кулоновском поле ядра, а в [233] полученные вероятности сравнивались с вероятностью слияния фотонов на электроне. Смирнов А.И. в работах [236, 237] рассчитал реакцию (3.58) для фотонов с разными частотами, но с параллельными импульсами. В вышеназванных работах [232, 233] эффект слияния фотонов изучался при помощи модели невзаимодействующих полей [183] на основе диаграммной техники Фейнмана-Дайсона при этом все частицы, участвующие в реакции (3.58) полагались неполяризованными, т.е. не изучались эффекты поляризации. В [233-237] совершенно не обсуждалась кинематика процесса, в то время, как частота конечного фотона является одной из экспериментально измеряемых физических величин.
|
|
|
Вообще говоря, если из всевозможных физических реализаций реакции слияния произвольных фотонов в один на электроне
 (3.59)
(3.59)
выбрать наиболее вероятную, когда все фотоны в начальном состоянии имеют одинаковое направление импульсов, а частоты могут быть произвольными, то реакцию (3.59) можно интерпретировать как излучение электрона в классическом или квантованном поле плоской электромагнитной волны определенного спектрального состава и поляризации. Однако в классической интерпретации поля плоской волны будет затруднительно рассмотреть реакцию (3.59) для фотонов одного направления, но с разными частотами и поляризациями. В модели, описывающей взаимодействие электрона с квантованной плоской волной произвольного спектрального состава и произвольной поляризации, эти трудности устраняются непосредственно в постановке задачи.
|
|
|
Другим примером множественного процесса, рассмотрение которого возможно провести в рамках модели "электрон + квантованная плоская волна", является процесс расщепления фотона на электроне
 (3.60)
(3.60)
где 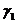 и
и 
 - фотоны плоской электромагнитной волны, а
- фотоны плоской электромагнитной волны, а  - излученный фотон.
- излученный фотон.
Аналогом данного процесса является двойной эффект Комптона. Отметим также то, что слияние двух фотонов в один на электроне можно рассматривать как обратную реакцию к двойному эффекту Комптона.
Впервые осуществление этого эффекта предсказано в работе [238]. В [239, 240] было рассчитано дифференциальное сечение данного эффекта для наиболее вероятного случая, когда один из вторичных фотонов жесткий, а другой - мягкий.
Наиболее полное описание двойного комптон-эффекта дано в [241], где получено и проанализировано общее выражение для дифференциального сечения эффекта, подробно изучаются различные частные случаи, угловые распределения и спектры энергии вторичных фотонов.
В [242] и [243] обсуждалась интерференция фотонов, т.е. ситуация, при которой оба излученных фотона имеют одни и те же энергию и импульс.
Во всех вышеуказанных работах расчеты производились на основе диаграммной техники Фейнмана-Дайсона и в предположении, что электрон в начальном состоянии покоится. Кроме того, в этих работах вероятности перехода получались при усреднении по спинам начальных частиц и суммировании по спинам конечных частиц, поэтому нельзя было исследовать эффекты поляризации.
Учет влияния поляризации был проведен в [244, 245]. В работах [246-252] двойной эффект Комптона изучался экспериментально.
Необходимо отметить, что процесс расщепления фотонов и двойной эффект Комптона отличаются друг от друга уже постановкой задачи.
А важнейшее отличие состоит в том, что фактически рассматривается излучение одного фотона с 4 - импульсом  , а фотон
, а фотон  принадлежит волне, т.е. рассматривается процесс излучения одного фотона с перестройкой спектра самой волны.
принадлежит волне, т.е. рассматривается процесс излучения одного фотона с перестройкой спектра самой волны.
Следует подчеркнуть, что, поскольку квантовая электродинамика является замкнутой теорией, и нельзя заранее утверждать об экспериментальном подтверждении её предсказаний, множественные процессы, примером которых и является слияние и расщепление фотонов на электроне, представляют собой ценную проверку квантовой электродинамики.
12.1 Модель квантовой электродинамики "электрон плюс квантованное поле плоской электромагнитной волны"
Исходное уравнение модели - одно частичное уравнение Дирака:
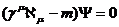 (3.61)
(3.61)
здесь  - матрица Дирака
- матрица Дирака
 - вектор состояния электрона в пространстве фотонных переменных,
- вектор состояния электрона в пространстве фотонных переменных,
 - потенциал свободного квантованного внешнего поля.
- потенциал свободного квантованного внешнего поля.
Как показано в [228], уравнение (3.61) является следствием точных уравнений квантовой электродинамики, записанных, например, в гейзенберговом представлении [253]:
где  ,
,  ,
,  - полевые операторы, а
- полевые операторы, а  - вектор состояния в гейзен6ерговом представлении. Если теперь в (3.62) прене6речь эффектами рождения электрон-позитронных пар, то из (3.62) можно получить (3.61).
- вектор состояния в гейзен6ерговом представлении. Если теперь в (3.62) прене6речь эффектами рождения электрон-позитронных пар, то из (3.62) можно получить (3.61).
Уравнение (3.61) точно решить не удается. Поэтому будем учитывать взаимодействие электрона не со всем полем излучения, а только с квантованной плоской волной, т.е. с фотонами, движущимися в одном направлении. Тогда в (3.61) заменим на оператор-потенциал
здесь  ,
,  ,
,  - частоты фотонов, занумерованных индексом K=1, 2, 3, … в порядке возрастания,
- частоты фотонов, занумерованных индексом K=1, 2, 3, … в порядке возрастания,  - орты поляризации
- орты поляризации
- операторы рождения и уничтожения фотонов частоты  и поляризации
и поляризации  , V – объём
, V – объём 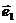 ,
, 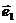 и
и  образуют правую тройку ортонормированных векторов декартовой системы координат.
образуют правую тройку ортонормированных векторов декартовой системы координат.
Уравнение (3.61) с оператором (3.63) будет исходным для модели электрон + квантованное поле плоской электромагнитной волны. Его точное решение находится методом разделения переменных: находятся такие волновые функции, которые являются собственными функциями операторов-интегралов движения, т.е. операторов, соответствующих физическим величинам, сохраняющимся во времени. Таким образом, отыскиваются так называемые чистые состояния, соответствующие сохранению определенных физических величин.
Решения уравнения Дирака (3.61) для электронов в поле квантованной плоской волны
где D – нормировочный множитель, унитарный оператор
 - целые числа (числа заполнения),
- целые числа (числа заполнения),
 - постоянный двух компонентный спинор описывает ориентацию спина электрона.
- постоянный двух компонентный спинор описывает ориентацию спина электрона.
Один из основных физических выводов состоит в том, что система из электрона, взаимодействующего с квантованной плоской волны, эффективно описывается в терминах невзаимодействующих квазичастиц: квазиэлектрона
с постоянным 4-вектором энергии-импульса  квазифотонов с 4-вектором энергии-импульса
квазифотонов с 4-вектором энергии-импульса  , причем энергия квазифотонов R связана с числами заполнения квазифотонов
, причем энергия квазифотонов R связана с числами заполнения квазифотонов  соотношением
соотношением
А частоты квазифотонов  определяются уравнением
определяются уравнением
Из (3.66) следует, что при выключении взаимодействия электрона с квантованным полем (  ) совокупность
) совокупность  частот квазифотонов должна перейти в совокупность
частот квазифотонов должна перейти в совокупность  частот свободных фотонов, т.е. с каждой частотой
частот свободных фотонов, т.е. с каждой частотой  можно сопоставить частоту квазифотона
можно сопоставить частоту квазифотона  .
.
Введенные квазифотоны обладают поляризацией. Связь чисел фотонов  с числами квазифотонов
с числами квазифотонов  линейная, и число фотонов одного сорта выражается через полный набор чисел квазифотонов, т.е.
линейная, и число фотонов одного сорта выражается через полный набор чисел квазифотонов, т.е.  , но в нулевом в
, но в нулевом в 
 порядке число фотонов равно числу квазифотонов.
порядке число фотонов равно числу квазифотонов.
Также и вакуумы фотонов и квззифотонов, не совпадающие в общем, совпадают в нулевом по  порядке.
порядке.
Как показано в [229], величина  пропорциональна параметру интенсивности классической волны
пропорциональна параметру интенсивности классической волны  (
(  - классический потенциал поля волны). Кроме того,
- классический потенциал поля волны). Кроме того,  пропорционально постоянной тонкой структуры, а величину
пропорционально постоянной тонкой структуры, а величину 
 можно понимать как плотность квазифотонов сорта
можно понимать как плотность квазифотонов сорта  , умноженную на постоянную тонкой структуры. Следовательно, параметром
, умноженную на постоянную тонкой структуры. Следовательно, параметром  можно характеризовать интенсивность поля квантованной плоской волны, и, рассматривая малые
можно характеризовать интенсивность поля квантованной плоской волны, и, рассматривая малые  , мы тем самым рассматриваем поле малой интенсивности.
, мы тем самым рассматриваем поле малой интенсивности.
Из рассмотрения интегралов движения в модели электрон + квантованная волна следует, что если в качестве независимых квантовых чисел выбрать  ,
,  ,
,  и спиновое квантовое число
и спиновое квантовое число  , энергия
, энергия  системы электрон + квантованная волна определяется однозначно из дисперсионного соотношения
системы электрон + квантованная волна определяется однозначно из дисперсионного соотношения 
При выключении взаимодействия (е=0) волновые функции (3.64) переходят в произведение функций свободного электрона и свободных фотонов. Если все числа заполнения  положить равными нулю, то получим волновую функцию электрона, взаимодействующего с частью электромагнитного вакуума, учтенного плоской волной.
положить равными нулю, то получим волновую функцию электрона, взаимодействующего с частью электромагнитного вакуума, учтенного плоской волной.
Для использования решений (3.64) в расчетах множественных процессов необходимым условием является полнота решений. Ортогональность и полнота волновых функций (3.64) строго доказана в [231] в формализме «нулевой плоскости» [254].
Проведенная выше классификация решений (3.64) позволяет ставить задачу о спонтанном переходе системы из одного состояния в другое с излучением одного фотона. Этот процесс схематично можно представить формулой:
Выбор начального и конечного состояний определяет конкретный вид реакции.
Дата добавления: 2018-02-18; просмотров: 551; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
