В. Часові характеристики найпростіших динамічних ланок
Розглянемо названі характеристики для різних типів динамічних ланок.
Підсилювальна ланка
Рівняння ланки:
. (6.11)
Передатна функція:
. (6.12)
Перехідна функція:
. (6.13)
Імпульсна перехідна функція (вагова функція):
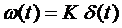. (6.14)
Перехідна та імпульсна перехідна характеристики показані на рис.6.4.
Рис. 6.4 - Перехідна та імпульсна перехідна характеристики підсилювальної ланки
Аперіодична ланка першого порядку (інерційна ланка)
Рівняння ланки:
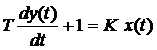. (6.15)
Передатна функція:
. (6.16)
Перехідна функція задовольняє рівнянню:
, (6.17)
при початковій умові 
.
Розв’язок рівняння (16) можна знайти різним шляхом. Використаємо розділення змінних:
. (6.18)
Виконавши інтегрування, матимемо
(6.19)
або
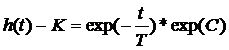. (6.20)
Використаємо початкову умову:
, (6.21)
звідки 
.
Розв’язок нашого рівняння, тобто перехідна функція аперіодичної ланки матиме вигляд
|
|
|
. (6.22)
Побудуємо графік. Вигляд його показано на рис.6.5, a). Цей графік має назву перехідної характеристики аперіодичної ланки.
Рис.6.5 – Часові характеристики аперіодичної ланки
а) - перехідна характеристика, б) - імпульсна перехідна характеристика.
Вагову функцію (імпульсну перехідну функцію) можна знайти за співвідношенням (6.10) 
.
Вона дорівнює
. (6.24)
Імпульсна перехідна характеристика (графік вагової функції) показана на рис.6.5 б).
Перехідна (а також імпульсна перехідна) характеристика повністю визначає аперіодичну ланку. Ланка має два параметри: коефіцієнт підсилення ланки К і постійну часу Т. З кожної характеристики можна визначити ці коефіцієнти. Коефіцієнт підсилення ланки дорівнює встановленому значенню вихідної величини на перехідній характеристиці, тобто значенню, яке має вихідна величина після завершення перехідного процесу. Постійну часу можна визначити як координату точки, в якій дотична до перехідної характеристики в початку координат перетинає лінію встановленого значення. Рівняння дотичної таке:
, (6.25)
при t = T вона перетне вісь абсцис.
y(t) =K . (6.26)
|
|
|
Аперіодична ланка першого порядку (ілюстрація використання методу операційного числення)
Розв’язати рівняння (6.16) для визначення перехідної характеристики можна також методом операційного числення. Для демонстрації методу операційного числення знайдемо розв’язок:
. (6.27)
Передатна функція рівняння
. (6.28)
Права частина рівняння дорівнює 1 при початковій умові 
x(t) = 1 . (6.29)
За таблицями перетворення Лапласа (таблиці оригінал – зображення) знаходимо зображення сигналу х(t)=1, яке дорівнює
х(р) = 1/p. (6.30)
Зображення перехідної знайдемо, помноживши передаточну функцію на зображення сигналу:
. (6.31)
Знову використаємо таблиці перетворень Лапласа (таблиці оригінал – зображення) і знаходимо вираз, який близький до (31), а саме:
. (6.32)
Щоб вираз (31) привести до вигляду (32), покладемо: a = - 1/T:
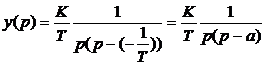. (6.33)
Отже розв’язок рівняння (оригінал) буде такий:
, (6.34)
|
|
|
що співпадає із найденим раніше розв’язком.
Щойно розглянутий метод розв’язання диференційного рівняння, а саме метод операційного числення, є універсальним. За його допомогою можна розв’язувати будь-які лінійні рівняння, тоді як використаний раніше метод розділення змінних придатний тільки для розв’язання невеликого числа рівнянь.
Коливальна ланка.
Диференційне рівняння ланки таке:
. (6.35)
Передатна функція
. (6.36)
Рівняння для визначення перехідної функції
(6.37)
з нульовими початковими умовами:
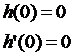(6.38)
Для знаходження перехідної функції треба розв’язати диференційне рівняння (37) з початковими умовами (6.38). Розв’яжемо його методом операційного числення. Зображення правої частини рівняння ми вже знаходили, воно записане формулою (30) х(р) = 1/p.
Отже зображення розв’язку рівняння (6.37) матиме вигляд
(6.39)
З таблиць перетворення Лапласа (таблиць оригінал-зображення) потрібно знайти оригінал для виразу (6.39), який і буде шуканим розв’язком рівняння. Можна скористатись будь-якими таблицями. Бажано мати таблиці, в яких розписані різні варіанти формул. Найпростіші таблиці незручні, тому що в них мало варіантів формул і потрібно робити ряд перетворень, щоб привести вираз до вигляду, який є в таблицях. Але можна скористатись будь-якими таблицями.
|
|
|
Дана формула в таблицях відсутня, але є інші формули, залежно від коренів знаменника (коренів характеристичного рівняння). Можливі такі випадки, а саме:
а. знаменник (характеристичне рівняння) має два комплексні корені;
б. два дійсні і різні корені;
в. два дійсні одинакові корені.
Найбільш цікавий випадок - це комплексні корені.
Запишемо характеристичне рівняння і обрахуємо його дискримінант.
; (6.40)
(6.41)
Уявні корені будуть, коли d < 1
У цьому випадку величина
.
Введемо позначення:
(6.42)
Зображення (39) розв’язку рівняння (37) запишемо у вигляді:
(6.43)
Згідно з таблицями зображення-оригінал знаходимо:
(6.44)
Тут не розписуємо значення величин А, В, α, щоб не загромаджувати виклад матеріалу.
Підставивши значення величин А, В, α, матимемо розв’язок
(6.45)
Графік рішення наведено на рис. 6.6.
Дійсні корені різні d > 1
Корені позначимо р1 і р2.
Зображення (39) розв’язку рівняння (37) запишемо у вигляді
. (6.46)
Згідно з таблицями перетворення Лапласа оригінал розв’язку матиме вигляд
. (6.47)
Тут
. (6.48)
У цьому випадку графік подібний до графіка аперіодичної ланки і таку ланку подекуди називають аперіодичною ланкою другого порядку.
Розглянемо перехідну характеристику коливальної ланки, тобто побудуємо графіки розв’язків рівняння для перехідної функції. Вигляд її показано на рис.6.6. Змінюючи Т, К, та D, можна одержати перехідні характеристики, які відповідають ланкам з різними параметрами. Експериментальні дослідження ланок ви виконували під час лабораторних робіт.
Рис 6.6 – Перехідна характеристика коливальної ланки (К=1; Т=0,1; d=0,1)
Інтегруюча ланка
Диференційне рівняння ланки таке:
(6.49)
Ланка називається інтегруючою тому, що вихідний сигнал дорівнює інтегралу від вхідного. Виконавши інтегрування правої і лівої частини по t, одержимо
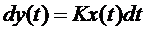; (6.50)
. (6.51)
Передатна функція
. (6.52)
(6.53)
Рівняння для визначення перехідної функції
(6.54)
з початковою умовою h(0) = 0
Розв’язок рівняння: 
. З початкової умови C = 0.
Отже
h(t) = Kt. (6.55)
Перехідна характеристика інтегруючої ланки – пряма ліній, нахилена під кутом з кутовим коефіцієнтом К.
Імпульсна перехідна характеристика
. (6.56)
Це горизонтальна пряма лінія на рівні К.
Диференційна ланка
Диференційне рівняння ланки таке:
. (6.57)
Ланка називається диференційною тому, що вихідний сигнал дорівнює похідній від вхідного сигналу.
Передатна функція
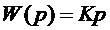. (6.58)
Рівняння для визначення перехідної функції
. (6.59)
Використавши співвідношення (5) для тета- та дельта-функцій одержимо:
. (6.60)
Тобто перехідна характеристика диференційної ланки має вигляд дельта функції. Цікаво розглянути також імпульсну перехідну характеристику диференційної ланки:
. (6.61)
Вигляд її показано на рис.6.7
Рис.6.7 – Похідна від дельта-функції.
Реальна диференційна ланка
Її диференційне рівняння таке:
. (6.62)
Передатна функція
. (6.63)
Рівняння для визначення перехідної функції
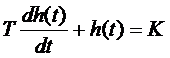(6.64)
з початковою умовою h(0) = 0.
Розв’яжемо рівняння методом операційного числення:
(6.65)
Згідно з таблицями перетворення Лапласа для оригінала перехідної функції маємо
. (6.66)
Перехідна характеристика – графік перехідної функції має вигляд
Рис.6.8 – Перехідна характеристика реальної диференційної ланки
Зробимо підсумок. Вище розглянуто часові характеристики динамічних ланок. Таких характеристик дві: перехідна й імпульсна перехідна. Перехідна характеристика – це графік вихідного сигналу при ступінчатому сигналі на вході. Назва перехідна характеристика зумовлена тим, що ця характеристика описує перехід системи від одного стану коли вхідний сигнал був нульовим, до іншого, коли сигнал став рівним певній величині. Перехідні характеристики є графіками перехідної функції h(t) , а імпульсні перехідні характеристики – вагової функції ω(t).
Тут розглянуто перехідні функції й перехідні характеристики основних типів ланок. Характеристики цих же ланок вивчаються експериментально під час лабораторних робіт. Єдине, зауваження до лабораторних робіт те, що їх виконують на комп’ютері і динамічну ланку позначають прямокутником. У реальних випадках це може бути певна електрична система, гідравлічна система чи механічний пристрій. Коефіцієнти ланки – це маса маховика, довжина стержня, пружність, індуктивність, ємність та інші характеристики реальних ланок.
Знання характеристик динамічних ланок потрібне для подальшого вивчення матеріалу, оскільки будь-яка система керування складається з певного числа динамічних ланок різних типів.
Дата добавления: 2018-02-15; просмотров: 1203; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!