Неоднорідне диференційне рівняння САК з постійними коефіцієнтами
Ми розглянули однорідне диференційне рівняння. Однорідне рівняння – це рівняння в якому права частина дорівнює нулю. У ТАК однорідне рівняння, відповідає системі, на яку не діють інші системи. Однорідне рівняння описує поведінку системи, представленої самій собі. Часто говорять, що однорідне рівняння описує власні коливання системи
Рис. 4.9 – Вхідна і вихідна величини системи автоматичного керування.
Загальний метод розв’язку однорідного диференційного рівняння – це використання підстановки Ейлера. Розв’язуючи однорідні рівняння САК ми одержали дуже важливу характеристику, а саме умову стійкості.
Розглянемо розв’язання неоднорідних рівнянь.
(4.24)
При нульових початкових умовах, а саме:
y(0) = 0; y’(0) = 0; y(2)(0) = 0;…, y(n-1)(0) = 0 (4.25)
Як відомо з математики, диференційне рівняння n-го порядку має n початкових умов. Нульові початкові умови означають, що сама функція і n-1 її похідні в початковий момент часу рівні нулю, що записано у вигляді (4.25).
Розв’язати це рівняння підстановкою Ейлера вже не можна, оскільки права частина рівняння не дорівнює нулю.
Розв’язання неоднорідного рівняння методом Лапласа
Для знаходження розв’язку неоднорідного рівняння застосовують перетворення Лапласа. Тут підстановка має більш складний вигляд. Пряме перетворення
. (4.26)
|
|
|
Зворотне перетворення
. (4.27)
Величина y(p) має свою назву, її прийнято називати зображенням функції y(t )за Лапласом або просто зображенням, а y(t) називають оригіналом функції. Аналогічно можна записати формули для оригіналу та зображення будь-якої функції, наприклад x(t) та x(p).
Для розв’язання рівняння (4.24) помножимо праву й ліву частини на величину 
і виконаємо інтегрування в межах від 0 до ∞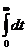 
, тоді матимемо:
(4.28)
Розглянемо окремі доданки в (4.28). Для доданка 
виконаємо інтегрування по частинах і використаємо початкові умови.
Правило інтегрування по частинах таке:
. (4.29)
Використовуючи його, одержимо:
.
Використавши початкову умову y(0) = 0, бачимо, що перші два доданки рівні нулю, і одержимо формулу
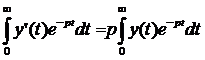. (4.30)
Наступний доданок в (5) приведе до такого співвідношення:
. (4.31)
Справді,
.
Використавши початкові умови та вираз (4.30), одержимо співвідношення (4.31).
Аналогічні співвідношення маємо для всіх похідних вищих порядків . Отже в результаті перетворень рівняння (4.24) набуде вигляду:
|
|
|
(4.32)
Винесемо за дужки спільний множник в правій і лівій частинах рівняння і матимемо:
(4.33)
Множники за дужками (інтеграли) згідно з використаною підстановкою (2) - це зображення вихідного y(p) та вхідного x(p) сигналів.
Отже приходимо до виразу
(4.34)
Тут:
. (4.35)
Величину х(р) прийнято називати зображенням (за Лапласом) вхідної величини x(t).
З (11) для зображення вихідної величини y(p) одержимо:
. (4.36)
Знайшовши зображення функції y(p) з рівняння (4.36) та виконавши зворотне перетворення (4.27), одержимо шуканий розв’язок неоднорідного диференційного рівняння (4.24) y(t):
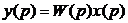(4.37)
Величина y(p) зв’язана з величиною x(p) алгебраїчним відношенням (4.36)
Величину W(p) у даному відношенні називають передатною функцією:
. (4.38)
Передатна функція
Визначення передатної функції таке:
Дата добавления: 2018-02-15; просмотров: 588; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!