Сингулярное разложение матрицы
Nbsp; § 4.3. Собственные значения и собственные векторы самосопряженного линейного преобразования
Общие свойства
Пусть  – евклидово пространство и
– евклидово пространство и  - самосопряженное преобразование в
- самосопряженное преобразование в  .
.
Теорема 4.6. Характеристическое уравнение самосопряженного отобра-жения имеет только действительные корни.
Доказательство. Пусть  – корень характеристического уравнения
– корень характеристического уравнения  и
и  – решение системы линейных алгебраических уравнений
– решение системы линейных алгебраических уравнений  , где матрица
, где матрица  является вещественной симметри-ческой матрицей:
является вещественной симметри-ческой матрицей:  ,
,  («
(«  » - значек комплексного сопряжения). Умножим равенство
» - значек комплексного сопряжения). Умножим равенство  слева на комплексно-сопряженный вектор-строку
слева на комплексно-сопряженный вектор-строку  :
:  . Отсюда
. Отсюда  . Знаменатель получившей-ся дроби – действительное число:
. Знаменатель получившей-ся дроби – действительное число:  . Числитель также действительное число, поскольку
. Числитель также действительное число, поскольку  , и, ввиду
, и, ввиду  и
и  ,
,  =
= 
 =
=  . Теорема доказана.
. Теорема доказана.
Следствие 1. Самосопряженное преобразование  имеет n собственных значений с учетом их кратности.
имеет n собственных значений с учетом их кратности.
Следствие 2. Вещественная симметрическая матрица  имеет n собственных значений с учетом их кратности.
имеет n собственных значений с учетом их кратности.
Теорема 4.7. Собственные векторы самосопряженного преобразования  , соответствующие различным собственным значениям, ортогональны.
, соответствующие различным собственным значениям, ортогональны.
Доказательство. Пусть  ,
,  – собственные векторы преобразования A, соответствующие собственным значениям
– собственные векторы преобразования A, соответствующие собственным значениям  :
:  ,
,  . Умножим первое равенство скалярно справа на
. Умножим первое равенство скалярно справа на  :
:  , а второе равенство скалярно слева на
, а второе равенство скалярно слева на  :
:  . Отсюда и из условия
. Отсюда и из условия  следует, что
следует, что  . Поскольку
. Поскольку  , то
, то  , т.е.
, т.е.  для
для  .
.
|
|
|
Следствие. Собственные вектор-столбцы симметрической матрицы, соответствующие различным собственным значениям, ортогональны.
Теорема 4.8. Если самосопряженное преобразование  имеет различные собственные значения
имеет различные собственные значения  , то в
, то в  существует ортонорми-рованный базис из n собственных векторов этого преобразования. В этом базисе матрица преобразования диагональна:
существует ортонорми-рованный базис из n собственных векторов этого преобразования. В этом базисе матрица преобразования диагональна:  .
.
Доказательство. Утверждение теоремы получаем на основании следствия из теоремы 4.2 и теоремы 4.7.
Справедливо следующее утверждение.
Теорема 4.9. Геометрическая кратность любого собственного значения самосопряженного преобразования равна его алгебраической кратности.(Без доказательства).
Следствие. Любая симметрическая матрица простая.
Простая матрица приводится к диагональному виду с собственными значениями на главной диагонали с учетом их кратности. Это дает возможность, в частности, очевидным образом решать вопрос о положительной определен-ности матрицы.
Теорема 4.10. Вещественная симметрическая матрица A размера  ранга
ранга  неотрицательно определена в том и только в том случае, когда A имеет r положительных собственных значений и
неотрицательно определена в том и только в том случае, когда A имеет r положительных собственных значений и  собственных значений, равных нулю. В частности, вещественная симметрическая матрица A определена положительно в том и в том случае, когда все ее собственные значения положительны.
собственных значений, равных нулю. В частности, вещественная симметрическая матрица A определена положительно в том и в том случае, когда все ее собственные значения положительны.
|
|
|
4.3.2. Свойства преобразования 
Пусть задано линейное отображение  и его сопряженное отображение
и его сопряженное отображение 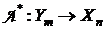 .
.
10. Преобразование  является самосопряженным и имеет неотрицательные собственные значения.
является самосопряженным и имеет неотрицательные собственные значения.
Самосопряженность следует из равенств  . Пусть теперь
. Пусть теперь  – собственное значение преобразования
– собственное значение преобразования  . Умножим равенство
. Умножим равенство  скалярно на x:
скалярно на x:  . Но
. Но  =
=  . Отсюда, в силу
. Отсюда, в силу 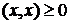 , следует неотрицательность
, следует неотрицательность  . Причем
. Причем  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Аналогично доказывается самосопряженность преобразования  .
.
20. Ядро преобразования  совпадает с ядром преобразования A:
совпадает с ядром преобразования A:  .
.
Из  следует, что
следует, что  . Поэтому
. Поэтому  . Обратно, если
. Обратно, если  , то
, то  . Отсюда
. Отсюда  и
и  . Утверждение доказано.
. Утверждение доказано.
Следствие. Квадратичная форма  неотрицательно определена. Она положительно определена тогда и только тогда, когда
неотрицательно определена. Она положительно определена тогда и только тогда, когда  .
.
30. Преобразования  и
и  имеют одинаковые ненулевые собственные значения с учетом их кратности.
имеют одинаковые ненулевые собственные значения с учетом их кратности.
Пусть  - собственное значение самосопряженного преобразования
- собственное значение самосопряженного преобразования  кратности
кратности  . По теореме 4.9 ему соответствует
. По теореме 4.9 ему соответствует  линейно независимых собственных векторов
линейно независимых собственных векторов  . Подействуем отображением
. Подействуем отображением  на левую и правую части равенства
на левую и правую части равенства  ,
,  . В результате получаем равенство
. В результате получаем равенство  , где
, где  . Так как по условию
. Так как по условию  , то из
, то из  следует, что
следует, что  . Таким образом,
. Таким образом,  - собственное значение, а
- собственное значение, а  – собственные векторы преобразования
– собственные векторы преобразования  .
.
|
|
|
Покажем, что векторы  линейно независимы. Для этого рассмотрим равенство
линейно независимы. Для этого рассмотрим равенство  . Действуя на это равенство преобразованием
. Действуя на это равенство преобразованием  и учитывая
и учитывая  , получаем:
, получаем:  =
= 
 =
=  = 0. Ввиду
= 0. Ввиду  последнее равенство может выполняться только при
последнее равенство может выполняться только при  . Следовательно, векторы
. Следовательно, векторы  линейно независимы. Поскольку преобразование
линейно независимы. Поскольку преобразование  , также как и
, также как и  является самосопряженным, то по теореме 4.9 геометрическая и алгебраическая кратности каждого его собственного значения совпадают. Отсюда следует сформулированное выше свойство.
является самосопряженным, то по теореме 4.9 геометрическая и алгебраическая кратности каждого его собственного значения совпадают. Отсюда следует сформулированное выше свойство.
Сингулярные числа и базисы
Сингулярные базисы
Первым сингулярным базисом  отображения A называется базис в пространстве
отображения A называется базис в пространстве  , состоящий из собственных ортонормированных векторов преобразования
, состоящий из собственных ортонормированных векторов преобразования  , если векторы
, если векторы  упорядочены в порядке убывания соответствующих собственных значений:
упорядочены в порядке убывания соответствующих собственных значений:  .
.
Если  , то
, то  при
при  и
и  при
при  . Первый сингулярный базис получается следующим образом: 1) отыскиваются собственные векторы
. Первый сингулярный базис получается следующим образом: 1) отыскиваются собственные векторы  преобразования
преобразования  ; 2) эти векторы нормируются; 3) полученная система векторов дополняется до ортонорми-рованного базиса в пространстве
; 2) эти векторы нормируются; 3) полученная система векторов дополняется до ортонорми-рованного базиса в пространстве  векторами
векторами  из
из  . Последнее указывает на то, что первый сингулярный базис
. Последнее указывает на то, что первый сингулярный базис  задан неоднозначно.
задан неоднозначно.
|
|
|
Имеем  . Отсюда следует, что
. Отсюда следует, что
 ,
,  . (4.9)
. (4.9)
Числа  называются сингулярными числами отображения A.
называются сингулярными числами отображения A.
Вторым сингулярным базисом  отображения A называется ортонормированный базис в пространстве
отображения A называется ортонормированный базис в пространстве  , первые r векторов которого определяются как
, первые r векторов которого определяются как  , а остальные векторы
, а остальные векторы  взяты из
взяты из  . Линейные оболочки систем векторов
. Линейные оболочки систем векторов  и
и  изоморфны друг другу.
изоморфны друг другу.
К определению сингулярных базисов можно подойти также следующим образом. Пусть 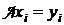 . Имеем
. Имеем  . Соотноше-ния
. Соотноше-ния 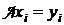 и
и  для
для  взаимно обратны. Если положить
взаимно обратны. Если положить  и
и  приходим к симметричным формулам
приходим к симметричным формулам  и
и  , из которых следуют соотношения, определяющие сингулярные базисы:
, из которых следуют соотношения, определяющие сингулярные базисы:

 (4.10)
(4.10)
Сингулярное разложение матрицы
Теорема 4.9. Вещественная матрица A размера  ранга
ранга  может быть представлена в виде
может быть представлена в виде
 , (4.11)
, (4.11)
где U - ортогональная матрица размера  , V - ортогональная матрица размера
, V - ортогональная матрица размера  ,
,  - матрица размера
- матрица размера  ,
,  .
.
Доказательство. Пусть матрица A представляет отображение  в паре ортогональных базисов
в паре ортогональных базисов  ,
,  . Существование искомого разложения (4.11) следует из теоремы 2.1. Укажем явный вид матриц U, V и D. В качестве U и V возьмем матрицы, столбцы которых выражают соответственно второй сингулярный базис
. Существование искомого разложения (4.11) следует из теоремы 2.1. Укажем явный вид матриц U, V и D. В качестве U и V возьмем матрицы, столбцы которых выражают соответственно второй сингулярный базис 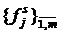 в базисе
в базисе  пространства
пространства  и первый сингулярный базис
и первый сингулярный базис  в базисе
в базисе  пространства
пространства  . Матрица D – это представление отображения
. Матрица D – это представление отображения  в сингулярных базисах.
в сингулярных базисах.
Осталось учесть, что для ортогональных матриц справедливо соотношение  . Теорема доказана.
. Теорема доказана.

Представление (4.11) называется сингулярным разложением матрицы.
Упражнения
1. Показать справедливость формулы (4.4).
2. Установить справедливость формул  , где
, где  – собственные значения матрицы A.
– собственные значения матрицы A.
3. Доказать, что всякая простая матрица подобна диагональной матрице.
4. Доказать теорему 4.7.
4. Доказать самосопряженность преобразования  .
.
5. В сингулярном разложении матрицы рассмотреть случаи различных соотно-шений между n, m и r.
6. Нарисовать схему, аналогичную схеме преобразования подобия, применительно к сингулярному разложению матрицы.
Дата добавления: 2018-02-15; просмотров: 1585; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
