Статическая обработка данных пассивного эксперимента. Множественный линейный регрессионный анализ

Множественный линейный регрессионный анализ

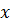На практике для обработки результатов наблюдений статистическими методами чаще используют множественный линейный регрессионный анализ. Однако из-за сложности расчета результатов исследований при действии нафункцию нескольких факторов , задачу упрощают и сводят ее к парнойрегрессии.

Таблица 1

Матрица заданий к проведению парной корреляционной связи

№ п/п	Наименование переменной			№ п/п	Наименование переменной
№ п/п	1	2	3	№ п/п	1	2	3
1	Х₁	Х₂	Х₃	14	Х₁₁	Х₁₄	Х₁₇
2	Х₄	Х₅	Х₆	15	Х₁₂	Х₁₅	Х₁₈
3	Х₇	Х₈	Х₉	16	Х₁₃	Х₁₆	Х₁₉
4	Х₁₀	Х₁₁	Х₁₂	17	Х₁₄	Х₁₇	Х₂₀
5	Х₁₃	Х₁₄	Х₁₅	18	Х₁₅	Х₁₈	Х₂₁
6	Х₁₆	Х₁₇	Х₁₈	19	Х₁₆	Х₁₉	Х₂₂
7	Х₁₉	Х₂₀	Х₂₁	20	Х₁₇	Х₂₀	Х₂₃
8	Х₂₂	Х₂₃	Х₂₄	21	Х₁₈	Х₂₁	Х₂₄
9	Х₂₅	Х₁	Х₄	22	Х₁₉	Х₂₂	Х₂₅
10	Х₂	Х₅	Х₈	23	Х₂₀	Х₂₃	Х₁
11	Х₁	Х₄	Х₇	24	Х₂₁	Х₂₄	Х₂
12	Х₃	Х₆	Х₉	25	Х₂₂	Х₂₅	Х₃
13	Х₁₀	Х₁₃	Х₁₆	26	Х₂₃	Х₁	Х₁₀

Вообще, при множественном линейном регрессионном анализе задача формируется как отыскание коэффициентов и в уравнении вида

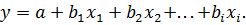(1.8)

Коэффициенты уравнения регрессии определяют методом наименьших квадратов, который заключается в подборе коэффициентов уравнения регрессии при которых соблюдается условие

где и – фактическое и расчетное значение функции в -ом опыте.

При большом объеме данных множественный линейный регрессионный анализ проводят с помощью ЭВМ. В случае, когда функция зависит от двух переменных, задача поиска уравнения регрессии упрощается. В этом случае предварительно определяют среднеквадратические отклонения и средние арифметические значения функции и переменных и , а также парные коэффициенты корреляции для всех возможных комбинаций между переменными , и : 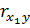, , . Уравнение регрессии имеет следующий вид

где коэффициенты и определяются по формулам:

Свободный член уравнения регрессии (1.8) может быть определен по формуле .Полученные коэффициенты необходимо подставить в формулу 1.8.

Адекватность уравнения регрессии проверяется по критерию Фишера по методике, описанной для парного линейного регрессионного анализа.

Задание 3.Получить уравнение множественной линейной регрессиирежима работы и показателей работы доменной печи.

Матрица заданий приведена в табл. 1 (принять: – 1 столбец, – 2, – 3), исходные данные к заданиям– приложение6, критические значения коэффициента парной корреляции – приложение 7, значения критерия Стьюдента – приложение 8.

Методы планирования эксперимента. Планы первого порядка

Если проводятся представленные эксперименты или априори известна прямолинейная зависимость между исследуемыми параметрами, то при планировании экспериментов используют планы первого порядка.

Для каждого переменного выбирается шаг варьирования . Если известны максимальное и минимальное значения переменной, тогда шаг варьирования равен

Причем большее значение переменной (верхний ряд) обозначается +1. Аналогично нижний уровень -1, средний (нулевой) уровень .

Исследования проводятся по плану-матрице планирования экспериментов. Она представляет собой возможные комбинации уровней. Все возможные комбинации уровней называются полным факторным экспериментом.

Если уровней 2 (верхний и нижний), а число переменных 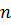, то количество опытов 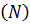при полном факторном эксперименте составляет: 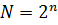, то есть при двух переменных необходимо провести 4 активных опыта, при трех – 8, при четырех – 16 и т.д.

План-матрица при двухи трехпеременных приведена в табл. 2 и 3.

Таблица 2

Матрица планирования для двух факторов

Опыт
1	+1	-1	-1
2	+1	+1	-1
3	+1	-1	+1
4	+1	+1	+1

После построения матрицы, приступают к проведению экспериментов. Причем каждый из опытов матрицы проводят не менее 2 раз. Это будут параллельные опыты. Эксперименты следует проводить в случайном порядке. Результатом эксперимента будет служить модель вида

Для получения модели необходимо определить коэффициенты, показывающие влияние каждого фактора на параметр оптимизации, по формуле

гдеj – номер фактора (j=0,1 … к);

– значение параметра оптимизации в i–ом опыте;

– кодированное значение j-го фактора в i-ом опыте;

– количество опытов.

Таблица 3

Матрица планирования для трех факторов

Опыт
1	-1	-1	-1
2	+1	-1	-1
3	-1	+1	-1
4	+1	+1	-1
5	-1	-1	+1
6	+1	-1	+1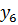
7	-1	+1	+1
8	+1	+1	+1

Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор на величину параметра оптимизации. Если коэффициент имеет знак (+), то это влияние положительное, и наоборот.

Полученная модель – является линейной, но фактически в выбранных интервалах варьирования факторов процесс может изменяться и не по линейному закону.

Задание 4.Постройте матрицу планирования двух факторного эксперимента, укажите максимальное , минимальное значения переменной и шаг варьирования , определите коэффициенты, показывающие влияние каждого фактора на параметр оптимизации.

В качестве плановых переменных и результата эксперимента следует принимать значения из табл. 1 ( –3 столбец, – 1, – 2), исходные данные к заданиям– приложение6.

Библиографический список

1. Кухаркина Т.В. Основы построения кинетических моделей: учебное пособие / Т.В.Кухаркина, Н.Г. Дигуров. –Москва: РХТУ им. Д.И. Менделеева, 1999. – 48 с.

2. РумшинскийЛ.З. Математическая обработка результатов экспериментов / Л.З. Румшинский. –Москва: Наука, 1971. – 192 с.

3. Тимофеев А.А. Методика исследования и обработки данных в литейном производстве: учебное пособие / А.А. Тимофеев. –Воронеж: Изд-во Воронежского политехнического института, 1981. – 80 с.

4. Львовский Е.Н. Статистические методы построения эмпирических формул: учеб. пособие для вузов /Е.Н. Львовский. –Москва: Высшая школа, 1988. – 239с.

5. Кнотек М. Анализ металлургических процессов методами математической статистики / М.Кнотек, Р.Войта, И. Шефц. –Москва: Металлургия, 1968. – 212с.

6. Новик Ф.С. Планирование эксперимента на симплексе при изученииматематических систем / Ф.С. Новик. –Москва: Металлургия, 1985. – 256 с.

7. Новик Ф.С. Математические методы планирования экспериментав металловедении / Ф.С. Новик. – Москва: МИСиС, 1970. –79 с.

8. Ковшов В.Н. Постановка инженерного эксперимента / В.Н. Ковшов. –Киев:Вища школа, 1982. –120с.

Приложение 1

Дата добавления: 2018-02-15; просмотров: 598; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!