Потоки платежей. Финансовая рента

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВПО «Брянский государственный технический университет» Кафедра «Высшая математика » Расчетно-графическая работа По дисциплине «Математическое моделирование в социологии» Выполнила: Студентка гр. 12-Сц Джурко Анастасия Проверил: Доцент каф. «ВМ», к.т.н. Белоусов Алексей Григорьевич Брянск 2013

Вариант 4

Задание №1:
Найти параметры линейной, квадратичной и степенной зависимости, используя метод наименьших квадратов. Составить задание, к приведенной таблице.

X	1	2	3	4	5
Y	2,5	3,9	6	7,4	9,9

Решение:

В средней школе проводилась контрольная работа среди 4ых классов, состоящая из 5 заданий. Данные записаны в таблице, где X – количество выполненных заданий, а Y-число учеников, выполнившие указанное количество заданий.

Параметры перечисленных зависимостей являются решениями систем линейных алгебраических уравнений. Для расчета коэффициентов систем заполним следующую таблицу:

i	x_i	y_i	x_iy_i	x²_i	x²_iy_i	x³_i	x⁴_i	u_i=lnx_i	v_i=lny_i	u_iv_i	u_i²
1	1	2,5	2,5	1	2,5	1	1	0	0,92	0	0
2	2	3,9	7,8	4	15,6	8	16	0,69	1,36	0,94	0,4
3	3	6,0	18	9	56	27	81	1,09	1,79	1,96	1,2
4	4	7,4	29,6	16	118,4	64	256	1,38	2	2,77	1,9
5	5	9,9	49,5	25	247,5	125	625	1,60	2,29	3,68	2,5
S	15	29,7	107,4	55	440	225	979	4,78	8,36	9,37	6,1

а) Рассмотрим линейную зависимость у=ах+b. Для этого воспользуемся следующей системой МНК (см. рис.1);

Рис. 1. система МНК для решения линейной зависимости

получаем следующую систему уравнений:

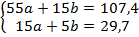
Решая эту систему, находим: а=1,83; b=0,45.

Подставляем a и b в линейную зависимость:

Y=1,83X+ 0,45

Находим, координаты точки, подставив в значение X произвольные точки (-2 и 4)

X	-2	4
y	-3,2	7,7

Затем, изображаем на координатной плоскости (в виде линейного графика) и отмечаем данные по условию точек (см. рис. 2)

Рис. 2. Графически изображенная, линейная зависимость.

б) рассмотрим квадратичную зависимость у=Ах²+Вх+С. Для этого воспользуемся следующей системой МНК (см. рис.3).

Рис.3. система МНК для решения , квадратичной зависимости

получаем следующую систему уравнений:

Решая систему методом Крамера, получим, что А=0,25; В=0,3 ; С=2,2

Подставляем A,B и С в линейную зависимость:

Y=0,25x²+0,3x+2,2

Изобразим графически:

Рис. 4. Графически изображена квадратичная зависимость

в) определим параметры степенной зависимости у=aх^k. Прологарифмировав обе части равенства, получим: .

Обозначим: u=lnx, v=lny, l=lna. Тогда получим линейную зависимость v=ku+l. Запишем систему уравнений относительно k и l, используя систему (1)
(см. рис.5):

Рис.5. система МНК для решения степенной зависимости

Используя результаты, записанные в таблице, получим систему уравнений

.
Из системы находим: k=0,2, l=1,7. Т.е. линейная зависимость имеет вид: v=0,2u+1,7.

Чтобы записать степенную зависимость, найдем 5,4. Таким образом, степенная зависимость имеет вид: у=5,4х^0,2.

Изобразим графически:

Рис. 6. Графически изображена степенная зависимость

Задание №2:

Год (X)	2003	2006	2009	2012
пользов. (Y)	47	62	94	?

С помощью метода наименьших квадратов (МНК) оценить количество пользователей интернета, говоривших на японском языке в 2012, если имеются данные за предшествующие годы:

Решение:

Для нахождения y(x)=2012 необходимо получить зависимость относительно имеющихся данных, основываясь на предположении, что она квадратическая. Для расчета коэффициентов систем заполним следующую таблицу:

X	Y	X⁴	X³	X²	X²*Y	X*Y
1	47	1	1	1	47	47
2	62	16	8	4	248	124
3	94	81	27	9	846	282
S	203	98	36	14	1141	453

Рассмотрим квадратичную зависимость: Y=Ax²+Bx+C. Для этого воспользуемся следующей системой МНК (см. рис. 1).

Рис.1. система МНК для решения , квадратичной зависимости

Получаем следующую систему уравнений:

Решая систему методом Крамера, получаем, что: A=8,5; B=-10,5: C=49.

Подставим А,В и С в линейную зависимость:

y=8,5x²-10,5x+49.

Подставим в значения x, точку x=4, получаем, что y(4)=143

Изобразим графически.

138, 369, 089 – реальные данные по количеству пользователей интернета в Японии.
Полученные данные не сильно отличаются от истинных; можно предположить, что задача решена верно.

Задание №3

Были получены следующие данные: оценки абитуриентов по математике и обществознанию (см. в решение). Необходимо: Рассчитать коэффициент корреляции между оценками по обществознанию и математике и сделать вывод; проверить утверждение, что в среднем уровень подготовки математики не отличается от уровня подготовки по обществознанию.

Решение:

Математика (X)	42	53	50	63	36	35	40	40	40	48
Обществознание (Y)	70	70	60	70	70	45	43	58	63	61

Запишем необходимые формулы для нахождения коэффицента корреляции и воспользуемся ими:

r= Cov(x;y)/S_x*S_y

Cov(x;y)= ∑(x_i-x)*(y_i-y)/n

S²=∑( x_i-x)²/n

x=(42+53+50+63+36+35+40+40+40+48)/10=44,7

y=(70+70+60+70+70+45+43+58+63+61)/10=61

S²_x=(7,2+68,8+5,3+334,8+75,6+94+22+22+22+10,8)/10=67,25

S_x=8,2

S²_y=(81+81+1+81+81+256+324+9+4+0)/10=91,8

S_y=9,5

Cov(x;y)=(-2,7*9+8,3*9+5,3*(-1)+18,3*9-8,7*9+9,7* 16+4,7*18+4,7*3-4,7*2+3,3*0)/10= =(-24,3+74,7-5,3+164,7-78,3+155.2+84,6+14,1-9,4+0)/10=37,6

r=37,6/(8,2*9,5)=37,6/77,9=0,4

Вывод: Связь между признаками слабая.

Для проверки утверждения об уровне подготовки, воспользуемся критерием Фишера; запишем соответствующую формулу и воспользуемся ей:

F=S²₁/S²₂

F=67,2/91,8=0,7

Для данной задачи, число степеней свободы равно 9 и 9

Воспользовавшись таблицей значений критерия Фишера (F-критерия) для уровня значимости a = 0.05, найдем значение F_табл.

F_табл.=3,18

F_выб.<F_табл.,значит, выдвинутую гипотезу можно считать верной. В среднем уровень подготовки математики не отличается от уровня подготовки по обществознанию

Задание №4

Можно ли утверждать, что существует связь между полом ребенка с одним из родителей, по соответствующим данным (см. решение).

Решение:

На кого из родитител. Пол больше ребенка похож	Папа	Мама	∑
Мальчик	25	22	47
Девочка	19	17	36
∑	44	39	83

Проверим данную гипотезу с помощью критерия c². Составим новую таблицу с теоретическими частотами, для этого воспользуемся формулой:

n_ij= (n_i.*n_.j)/n

На кого из родитител. Пол больше ребенка похож	Папа	Мама	∑
Мальчик	24,9	22	47
Девочка	19	16,9	36
∑	44	39	83

Теперь, вычислим c²по формуле:

c²=

c²_выб.=(25-24,9)²/24,9 + (22-22)²/22 + (19-19)²/19 + (17-16,9)²/16,9= 0,0004+0,0005=0,0009.

Число степеней свободы равно 1.

Теперь, воспользуемся табличными значениями, считая, что уровень значимости равно 0,05.

c²_табл.= 0,0039

c²_табл >c²_выб , значит рассматриваемые признаки независимы.

Вывод: связи между полом ребенка с одним из родителей не существует.

Задание №5

а) Проводилось исповедование, в рамках которого рассматривался вопрос, какие дети лучше учатся – те, чьи способности оцениваются, как средние и высокие, или дети, которые, считаются очень одаренными. В качестве одного из показателей рассматривался разброс получаемых оценок. Были получены следующие результаты (см. решение) Можно ли считать, что разброс оценок в двух совокупностях одинаковый, используя критерий Фишера?

б) Имеется следующая выборочная статистика наблюдений среднесуточной летней температуры в Москве 1985 и 2005 гг. (см. решение). Можно ли утверждать, используя критерий Стьюдента, что средний уровень летней температуры в Москве не изменился?

Решение:

Предполагаемый уровень способностей	Оценки
Средний и высокий	89, 75, 60, 91, 77, 82, 71, 68
Очень высокий	87, 35, 96, 41, 89, 30, 97

Поставленную задачу, необходимо решать критерием Фишера, запишем для этого необходимые формулы и воспользуемся ими.

F=S²₁/S²₂

S²=∑( x_i-x)²/n

x=(89+75+60+91+77+82+71+68)/8=76,6

y=(87+35+96+41+89+30+97)/7=67,8

S²_x=(153,7 +2,56+275,5+179,5+0,1+29,1+31,3+73,9)/8=93,2

S²_y=(368,6+1075,8+795,2+718,2+449,4+1428,8+852,6)/7=812,6

F=93,2/812,6=0,11.

Число степеней свободы равно 7 и 6.
Теперь найдем F_табл.

F_табл.= 4.21

F_выб.<F_табл.,значит, выдвинутую гипотезу можно считать верной.

Вывод: Разброс оценок в двух совокупностях одинаковый.

б)

1985	2005
20,1	17,1
15,3	19,5
17,9	24
23,5	16,3
18,7	15,7
21,4	18,5
16,8	20,2
18,2	21,7

Поставленную задачу, необходимо решать критерием Стьюдента, запишем для этого необходимые формулы и воспользуемся ими.

t_n-1=D/(S_p/ )

D=∑Di/n

S_p=

D=(3-4,2-6,1+7,2+3+2,9-3,4-3,5)/8=-0,13

S²_p=156,7-(1,21/7)=156,7-0,1=156,6

S_p=12,5

t_n_-1=-0,13/(12,5/2,8)=-0,13/4,4=-0,02

Зная, что n=8, а a=0,8 получим данные по Таблице значений критерия Стьюдента (t-критерия)

t_n_-₁₍_табл)= 1.3

Сравним значения:

- t_n_-1(табл)< t_n_-1(выб.)< t_n_-1(табл)

-1,3<-0,02<1,3

Неравенство выполняется, значит, гипотеза верна.

Вывод: средний уровень летней температуры в Москве не изменился.

Эссе
на тему:
Использование понятие предела в социально-экономических расчетах.

В последнее время появилось большое количество учебных заведений, учащиеся которых выбирают экономические специальности в качестве своей дальнейшей деятельности. Как правило, преподаватели, работающие в таких заведениях, дают учащимся более глубокие знания по обычным темам учебного курса математики .При такой организации обучения рассматриваются экономические приложения той или иной темы, уделяется применению математического моделирования к решению экономических задач. Не является исключением и тема, посвященная приложениям определенного предела в других областях знаний.

Как правило, предел функции (предельное значение функции) в заданной точке, является предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция оказывается непрерывной (в данной точке).

Предел функции — одно из основных понятий математического анализа.

В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал и т. д.). Время - дискретная переменная. В некоторых случаях - в доказательствах и расчетах, связанных с непрерывными процессами, возникает необходимость в применении непрерывных процентов. Рассмотрим формулу сложных процентов:

S = P(1 + i)ⁿ.

Здесь P - первоначальная сумма, i - ставка процентов (в виде десятичной дроби), S - сумма, образовавшаяся к концу срока ссуды в конце n-го года. Рост по сложным процентам представляет собой процесс, развивающийся по геометрической прогрессии. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов. В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется, а проценты в виде разности S - P называются дисконтом. Величину P, найденную дисконтированием S, называют современной, или приведенной, величиной S. Имеем:

Р= Р= = 0.

Таким образом, при очень больших сроках платежа современная величина последнего будет крайне незначительна. В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов) определяется прежде всего тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процессов более адекватно, чем на основе дискретных. Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году:

S =P (1 + i/m) ^mn.

Наращенная сумма при дискретных процессах находится по этой формуле, здесь m - число периодов начисления в году, i - годовая или номинальная ставка. Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m → ∞ имеем:

S = P (1 + i/m) ^mn = P ((1 + i/m) ^m ) ⁿ.

Поскольку (1 + i/m) ^m = e ⁱ, то `S = P eⁱⁿ.

При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста, которая характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени. При непрерывной капитализации процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и номинальной ставки процентов. Для того, чтобы отличить ставки непрерывных процентов от ставки дискретных процентов, обозначим первую через d, тогда S = Pe.

Сила роста d представляет собой номинальную ставку процентов при m→ ∞. Множитель наращения рассчитывается с помощью ЭВМ или по таблицам функции.

Потоки платежей. Финансовая рента

Контракты, сделки, коммерческие и производственно-хозяйственные операции часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Отдельные элементы такого ряда, а иногда и сам ряд платежей в целом, называется потоком платежей. Члены потока платежей могут быть как положительными (поступления), так и отрицательными (выплаты) величинами. Поток платежей, все члены которого положительные величины, а временные интервалы между двумя последовательными платежами постоянны, называют финансовой рентой. Ренты делятся на годовые и р-срочные, где р характеризует число выплат на протяжении года. Это дискретные ренты. В финансово-экономической практике встречаются и с последовательностями платежей, которые производятся так часто, что практически их можно рассматривать как непрерывные. Такие платежи описываются непрерывными рентами.

Дата добавления: 2018-02-15; просмотров: 523; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!