Изучение земной поверхности. Построение
Топографического плана с помощью школьного
Нивелира
Цель работы: овладение навыками топографической съёмки местности с помощью «школьного» нивелира и вычерчивание топографического плана холма (карьера).
Оборудование: мерная лента, «школьный» нивелир, геодезические вешки и колышки, измерительные и чертёжные инструменты.
Порядок работы
1. С помощью «школьного» нивелира (высота инструмента – 1 м) и мерной ленты определить места расположения горизонталей и расстояния между горизонталями на склоне холма (карьера).
2. На основании полученных результатов вычертить топографический (в горизонталях) план объекта согласно индивидуального задания, которое определяется содержанием прил. 1 и 5 (масштаб горизонтальный 1:1000; масштаб вертикальный 1:100; сечение горизонталей – 1 м) (пример приведён в прил. 11).
3. Построить профиль холма (карьера) по линии «запад – восток», для чего необходимо последовательно, с учётом сечения горизонталей и принятого масштаба, отпускать перпендикуляр из мест пересечения прямой «запад – восток» с горизонталями на некую начальную прямую (нулевая горизонталь). Горизонтали вычерчиваются красным цветом. Уклон местности показывается бергштрихами (тоже красного цвета). Внутренняя ситуация наносится в соответствии с принятыми условными обозначениями. Если на чертеже отдельные высотные пояса отразить каким-то цветом, то такой план называется гипсометрическим (пример).
|
|
|
Вывод.
Работа 6
Изучение земной поверхности.
Линейная нивелирная съёмка
Цель работы: приобретение навыков линейной нивелирной съёмки местности (как правило, используется при проектировании дорог, трубопроводов и т.п.).
Оборудование: нивелир 2Н-10Л, нивелировочные рейки, мерная лента, геодезические вешки и колышки.
Порядок работы
1. Произвести пикетаж трассы (разбивка линии на отрезки длиной 100 м и закрепление их на местности колышками) с помощью какого-либо угломерного инструмента (в том числе и нивелира) и мерной ленты.
2. Определить абсолютную отметку пикета 0 (относительно ближайшего репера).
3. Определить чёрные отметки на пикетах с помощью нивелира и нивелировочных реек.
4. Определить красные отметки как разность между значениями чёрных отметок соседних пикетов (красная отметка нулевого пикета принимается за 0,00).
5. Определить отметки земной поверхности относительно отметки пикета 0.
6. Обосновать необходимый уклон будущей трассы.
7. Определить плановые отметки в соответствии с выбранным уклоном трассы.
8. Определить рабочие отметки как разность между отметками земной поверхности и плановыми отметками.
|
|
|
9. На основании индивидуального задания (прил. 1 и 6) вычертить на миллиметровке профиль нивелирной съёмки (горизонтальный масштаб 1:10 000, вертикальный масштаб 1:100) (пример приведён в прил. 11).
Вывод.
Работа 7
Изучение земной поверхности. Масштаб
Цель работы: приобретение навыков определения расстояний и площадей на местности по её изображению на планах и картах.
Оборудование: планиметр, курвиметр, палетка, планы, карты, чертёжные и измерительные инструменты.
Порядок работы
1. В соответствии с индивидуальным заданием (прил. 1 и 7) вычертить на бумаге график функции (в общем виде заданной уравнением параболы второго порядка) у = ах2 + bx + c. Для построения графика нужно определить минимум функции, т.е. найти первую производную: y’ = 2ax + b. Пример дан в прил. 11.
2. В соответствии с индивидуальным заданием выделить на чертеже криволинейную трапецию OABC, определить её площадь и длину кривой и прямой АВ. Для определения длины кривой АВ можно использовать уравнение
l = ∫ 
dx.
Подкоренное выражение здесь также имеет вид уравнения параболы второго порядка ax2 + bx + c. Приняв последнее выражение за М и введя дополнительные показатели
|
|
|
Δ = 4ac – b2 и k = 4a / Δ,
длину кривой можно определить по уравнению
∫ 
dx = (2ax + b) 
/ 4a + (1/2k)∫dx / ,
но так как ∫dx / = (1/ 
) ln (2 
+ 2ax + b), уравнение приобретает вид
∫ dx = (2ax + b) / 4a +
+ (1/2k)(1/ ) ln(2 + 2ax + b) ,
а в нашем случае длина кривой может быть рассчитана через нахождение интеграла:
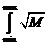dx ={[(2ax – b) 
] / 4a + [(4ac + b2) / 8a]×
×(1/ ) ln(2 
} 
,
так как
∫ dx = F(max) – F(min).
Длину кривой АВ требуется измерить нитью и линейкой, а также с помощью курвиметра.
Длину прямой АВ, в свою очередь, можно определить с помощью курвиметра, с помощью линейки и алгебраически, применяя теорему Пифагора.
Площадь криволинейной трапеции (S) определяется путём её разбивки на простейшие геометрические фигуры и вычисления суммарной площади этих фигур. Другой способ – использование палетки или планиметра. Но самый точный результат даёт, конечно, алгебраический метод расчёта площади путём нахождения определённого интеграла на отрезке ОС, т.е. с использованием уравнения Ньютона-Лейбница, что особых усилий не требует.
S = 
dx = F(max) – F(min),
|
|
|
в нашем случае
S = 
= 
.
3. Результаты измерения, полученные различными способами, соотнести с рассчитанными алгебраически. Ошибку выразить в процентах.
4. Результаты расчёта представить в виде следующей таблицы:
Таблица 4
Дата добавления: 2018-02-15; просмотров: 904; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!