Дискретизации непрерывного спектра произвольной последовательности

N-точечное ДПФ произвольной последовательности с непрерывным спектром представляют собой результаты частотной дискретизации спектра этой последовательности.

При изучении временной дискретизации мы видим, что при невыполнении определенных условий, задаваемых теоремами Котельникова, она приводит к взаимному перекрытию отдельных спектров в частотной области. Рассмотрим, что происходит при частотной дискретизации.

Вычислим N-точечное ДПФ произвольной последовательности заданной своим непрерывным спектром. По аналогии с (3.12) имеем

                                       (3.15)

В отличие от (3.12) пределы суммирования здесь взяты бесконечными, так как рассматриваем произвольную последовательность, которая может быть и бесконечной.

Положим, что последовательность значений , определяемая (3.15), представляет собой спектр  некоторой периодической последовательности , которая на периоде  может быть найдена с помощью ОДПФ согласно(3.11):

.

Подставляя в это соотношение вместо X_p(nω) значения X(e^jω_n),  определяемые равенством (3.15), и проделывая необходимые преобразования, можно показать, что

.                                (3.16)

Таким образом, найденная нами периодическая последовательность представляет собой сумму смежных и наложенных копий исход­ной последовательности {x(k∆t)}. При этом в зависимости от длины L последовательности возможны три случая, проиллюстриро­ванные на рисунке а, б, в, г, д. При L<N и L=N (рисунки а,б), т.е. когда число отсчетов последовательности не превышает размера ДПФ, на­ложения отдельных слагаемых суммы (3.16) не происходит и по последовательности {х_р(k∆t)} с помощью временного окна можно точно восстановить {x(k∆t)}.

При L>N (рис. в,г,д) отдельные слагаемые суммы (3.16) накладываются друг на друга, поэтому по последовательности {х_р(k∆t)} невозможно точно восстановить {x(k∆t)}.

 Таким образом, дискретизация в частотной области может при­вести к наложению частных последовательностей {x[(k-rN)∆t]} во временной области. Это происходит, если не выполняется ус­ловие L, где N - число отсчетов дискретизированного спектра последовательности {x(k∆t)}, L - число этой после­довательности.

Выводы. Основные результаты, полученные в пп. 3.1.2.1 −  3.1.2.5, можно сформулировать следующим образом:

1. Произвольная периодическая последовательность имеет непрерывный периодический спектр с периодом , описываемый дискретным рядом Фурье (3.6).   

2. Периодическая последовательность с периодом T=N∆t, включающим N отсчетов, имеет дискретный периодический спектр с периодом , описываемый ДПФ (3.10), причем в периоде спектра содержится N отсчетов.

3. Непериодическая последовательность конечной длины из N отсчетов, имеющая непрерывный спектр, точно описывается своим N-точечным ДПФ, так как по N отсчетам этого преобразования можно построить периодическую последовательность {х_р(k∆t)} из неперекрывающихся частных последовательностей {x[(k-rN)∆t]},  из которой с помощью временного окна может быть выделена ис­ходная последовательность {x(k∆t)}.

4. Последовательности конечной длины из L  отсчетов или бесконечная последовательность не может быть точно восстановлена по своему N-точечному ДПФ, так как по N   отсчетам этого преобразования можно построить только периодическую последовательность {х_р(k∆t)} из перекрывающихся частных по­следовательностей {x[(k-rN)∆t]}, из которой нельзя выделить исходную последовательность {x(k∆t)} с помощью какого-либо временного окна.

 

Рисунок 2.8

 

 

Свойства ДПФ

1) Свойство линейности.

Если {х_р(k∆t)} и {у_р(k∆t)} - периодические последова­тельности с периодом в N отсчетов каждая, а X_p(nω) и Y_p(nω) - их ДПФ, то последовательность

будет иметь ДПФ .

Это свойство справедливо и для любых непериодических после­довательностей конечной длины.

2. Свойство сдвига.

Если последовательность {х_р(k∆t)} периодическая, с периодом в N отсчетов, а ее ДПФ - X_p(nω), то ДПФ периодической после­довательности вида {x_р[(k-k₀)∆t]}  будет равно .

Если k₀=N, то ДПФ не изменится, так как .

Данное свойство справедливо и для непериодической последова­тельности конечной длины, однако в этом случае следует учиты­вать специфический характер временного сдвига последователь­ности. На рисунке а) с кружочком изображена конечная: последо­вательность {x(k∆t)} длиной в N отсчетов. Там же крестика­ми изображены отсчеты эквивалентной периодической последова­тельности {х_р(k∆t)}, имеющей то же ДПФ, что {x(k∆t)}. Чтобы найти ДПФ сдвинутой последовательности {x[(k-k₀)∆t]}, причем k₀<N, следует рассмотреть сдвинутую периодическую последовательность {x_р[(k-k₀)∆t]} и в качестве эквивалентной сдвинутой последовательности (имеющей ДПФ 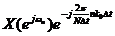) принять отрезок последовательности {x_р[(k-k₀)∆t]} в интервале  (рис. б)). Таким образом, с точки зрения ДПФ по­следовательность {x[(k-k₀)∆t]} получается путем кругового сдви­га элементов последовательности {x(k∆t)} на k₀ отсчетов.

 

3. Свойство симметрии.

Если периодическая последовательность {x_p(k∆t)} с периодом в N отсчетов является действительной, то ее ДПФ X_p(nω) удовлетворяет следующим условиям симметрии:

                                                                    (3.17)

Аналогичные равенства справедливы для конечной действитель­ной последовательности {x(k∆t)}, имеющей N -точечное ДПФ X(nω).

Равенства (3.17) означают, что реальная часть и модуль ДПФ на периоде [0 … ] будут всегда симметричны относительно частоты , а мнимая часть и аргумент – антисимметричны (т.е. симметричны противоположными знаками) относительно этой частоты (рисунок 2.10 а,б). Если к тому же сама последовательность {x_p(k∆t)} симметрична на периоде [0 … (N-1)∆t] относительно момента (N/2)∆t, т.е. x_p(k∆t)=x_р[(N-k)∆t] (рисунок 2.10, в), то ее ДПФ будет только действительной функцией частоты.

 

Рисунок 2.10

Данное свойство справедливо и для последовательностей конеч­ной длины.

 

 

Быстрое преобразование Фурье

3.1.2.7.1. Вводные замечания. Вывод базовых формул алгоритма "с прореживанием по времени"

При обработке сигналов во многих случаях приходится опре­делять спектры. При этом вычисление ДПФ последовательности ко­нечной длины непосредственно с помощью выражения (2.16) является достаточно трудоемкой процедурой. Действительно, для определения по этой формуле одного отсчета ДПФ нужно выполнить N комп­лексных умножений и (N-1) сложений, а для вычисления всего спектра (N отсчетов) – N² умножений и N(N-1) сложений. Вместе с тем существуют возможности такой организации процесса вычисления ДПФ, при которой число необходимых операций сложения и умножения существенно уменьшаются. Алгоритмы, реализующие эти возможности, называются быстрыми преобразованиями Фурье (БПФ). Эти алгоритмы не являются новым математическим средством списания сигналов, а представляют собой всего лишь экономный способ вычисления обычного ДПФ.                                                               

Основная идея БПФ состоит в том, чтобы разбить исходную последовательность, содержащую N отсчетов на две более короткие, ДПФ которых могут быть скомбинированы таким образом, чтобы получилось ДПФ исходной последовательности. Например, если N -четное, а исходная последовательность разбита на две, содержащие по N/2 отсчетов, то для вычисления искомого N-точечного ДПФ потребуется порядка (N/2)²2=N²/2 комплексных умножений, т.е. вдвое меньше по сравнению с прямым вычислением. Здесь множитель (N/2)² дает число умножений, необходимое для прямого вычисления N/2 -точечного ДПФ, а множитель 2 соответ­ствует двум ДПФ, которые должны быть вычислены. Эту операцию можно повторять, вычисляя вместо N/2-точечного ДПФ два N/4-точечных ДПФ (если N/2-четное) и сокращая тем самым объем вычис­лений еще в два раза. Выигрыш в два раза является приближенным, поскольку при его обозначении мы не учитывали, каким образом из ДПФ меньшего размера образуется искомое N -точечное ДПФ.

Рассмотрим подробнее один из возможных алгоритмов БПФ. Для удобства записей введем новое обозначение. Примем, что

.                                            (3.18)

С учетом этого формула (3.12) принимает вид

                                                      .                                  (3.19)

Положим, что последовательность {x(k∆t)}  содержит N отсчетов, причем N=2^l, т.е. равно целой степени числа 2. Введем две N/2 -точечные последовательности {x₁(k∆t)}   и {x₂(k∆t)}  из четных и нечетных членов последовательности {x(k∆t)} соответственно:

                                                                  (3.20)

N-точечное ДПФ исходной последовательности можно записать так:

.                    (3.21)

Первая сумма в правой части полученного соотношения объеди­няет все четные слагаемые выражения (3.19), а вторая – все нечетные.

Возводя обе части равенства (3.18) в квадрат, имеем:

.

Поэтому  и .

Используя данные соотношения, а также учитывая (3.20), равенство (3.21) можно записать в виде

.

Но первая сумма в этом выражении есть N/2 -точечное ДПФ последовательности {x₁(k∆t)}− X₁(e^jω_n), а вторая − N/2 -точеч­ное ДПФ {x₂(k∆t)} −  X₂(e^jω_n).

Поэтому

.                             (3.22)

Таким образом, N-точечное ДПФ исходной последовательности {x(k∆t)} может быть разложено на два (N/2) -точечных ДПФ, резуль­таты которых объединяются согласно (3.22). В выражениях для X₁(e^jω_n) и X₂(e^jω_n) n изменяется от 0 до ((N/2)-1), так как сами последовательности {x₁(k∆t)}  и {x₂(k∆t)}   имеют по N/2 отсчетов. Результат же X(e^jω_n) является N-точечным поэтому формулу (3.22) необходимо доопределить, т.е. добавить выражение для определения X(e^jω_n) при .

С учетом периодичности ДПФ это легко сделать, записав:

 Используя (3.18), легко показать, что

С учетом этого последнее выражение для X(e^jω_n) принимает вид                                 (3.23)

Выражение (3.23) определяет алгоритм БПФ, называемый алгоритмом "с прореживанием по времени", поскольку в этом алгоритме производится пересортировка значений входного сигнала (во временной области). Существует алгоритм "с прореживанием по частоте", где пересортируются выходные данные.

 

---

Дата добавления: 2018-02-15; просмотров: 644; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!