Преобразование Фурье (комплексный спектр) произвольной последовательности
Раздел 3. Основы цифровой обработки сигналов
§ 3.1.Математическое описание дискретных сигналов
3.1.1. Последовательности
Строгой математической моделью дискретного сигнала является взвешенная последовательность d-функций
(3.1)
(см. лекции по курсу ТИ). Однако в теории дискретных систем удобнее характеризовать каждый отсчет такого сигнала 
конкретным числом, равным значению отсчета, выраженному в принятых единицах измерения. При этом весь дискретный сигнал представляется в виде последовательности.
Под последовательностью будем понимать совокупность чисел, появляющихся в определенные пронумерованные моменты времени. Эти числа называются отсчетами.
Номера отсчетов последовательности представляют собой целые числа, выбираемые из интервала 
.
Последовательность можно изобразить графически так, как показано на рисунке 2.1.
Рисунок 2.1
Обозначается последовательность так:
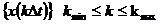
или просто
Во втором случае указание пределов изменения k обязательно, поскольку без него обозначение 
означает один k-й отсчет.
Последовательность, содержащая конечное число отличных от нуля отсчетов, называется последовательностью конечной длины.
Если последовательность 
имеет ненулевые отсчеты, расположенные только на положительной полуоси, т.е. на интервале 
, то она называется физически реализуемой или каузальной.
|
|
|
Если последовательность имеет хотя бы одно ненулевое значение и на отрицательной полуоси времени, то она называется физически реализуемой. В практических задачах физически нереализуемые последовательности не встречаются, но при рассмотрении некоторых теоретических вопросов представляют интерес.
Последовательность называется действительной, если все отсчеты ее являются действительными числами.
Последовательность называется периодической с периодом N, если значения отсчетов не меняются при изменении их номера на любое число, кратное N.
Рассмотрим наиболее часто встречающиеся последовательности. Простейшая последовательность ─ единичный отсчет
(3.2)
Задержанный на время единичный отсчет определяется как
а опережающий единичный отсчет
Все три последовательности изображены графически на рисунке 2.2.
Рисунок 2.2
Единичный отсчет в теории дискретных систем играет ту же роль, что и d-функция в теории непрерывных систем.
Вторая элементарная последовательность ─ единичный скачок
(3.3)
|
|
|
График этой последовательности приведен на рисунке 2.3.
Рисунок 2.3
Задержанный 
и опережающий 
во времени единичный скачок определяются как
и
Единичный скачок можно выразить через единичный отсчет с помощью соотношения
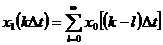(3.4)
Используя единичный отсчет, можно записать выражение, определяющее произвольную последовательность:
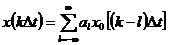(3.5)
Данное выражение отличается от формулы (3.4) тем, что расширены пределы суммирования (учтен случай физически нереализуемой последовательности) и введены масштабирующие коэффициенты 
, каждый из которых численно равен значению соответствующего отсчета .
Существуют и комплексные последовательности, отсчеты которых представляют собой комплексные числа. Важным примером таких последовательностей является комплексная экспонента.
Графическое представление таких последовательностей возможно двумя способами:
1) графическое изображение реальной и мнимой последовательности на отдельных графиках;
2) изображение отсчетов последовательности в комплексной плоскости.
Последний способ иллюстрирован на рисунке 2.4 применительно к последовательности (2.5).
|
|
|
Рисунок 2.4
Спектры последовательностей
Преобразование Фурье (комплексный спектр) произвольной последовательности
Для того, чтобы получить формулу, связывающую значения спектра последовательности 
непосредственно с отсчетами последовательности . Такую формулу можно получить, применив преобразование Фурье к выражению (3.1)
Используя фильтрующие свойства d-функции (см. лекц. по теор. инф. и практич. занятие на тему «Преобр. Фурье»), получим:
В результате окончательно имеем
(3.6)
Выражение (3.6) называется дискретным рядом Фурье и определяет прямое преобразование Фурье произвольной последовательности . Для того, чтобы найти ее обратное преобразование Фурье, проведем следующие рассуждения.
Как известно (см. . лекц. по теор. инф), спектр дискретизированного сигнала является периодической функцией частоты с периодом 
( 
и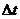 
соответственно круговая частота и шаг дискретизации). Поэтому на своем периоде эта функция может быть разложена в ряд Фурье, следующим образом:
, (3.7)
где
. (3.8)
|
|
|
Сравнивая выражения (3.7) и (3.6), можно заключить, что 
. Следовательно, с учетом (3.8), имеем
(3.9)
Полученное соотношение выражает обратное преобразование Фурье последовательности 
.
Рассматривая выражение (3.6), можно заключить, что спектр произвольной последовательности является непрерывным (сплошным) (спектральные составляющие присутствуют на всех частотах).
Дата добавления: 2018-02-15; просмотров: 1453; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!