Метод компромисса «точность-надежность» в анализе экономических временных рядов.
Nbsp; МОСКОВСКИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)
Экономико-аналитический институт
Отчет по курсу «Эконометрика»
Выполнила студентка группы_У07-721_
Лоншакова Виктория.
МОСКВА 2012г.
Временные ряды
Свойства Гаусса:
1. mδt=0;
2. σδ2=const;
3. r1=0.
Если эти свойства выполняются, то ошибку измерения можно считать белым шумом.
Метод наименьших квадратов
Теорема Гаусса-Маркова:
Если в линейной по параметрам регрессии факторы неслучайны и линейно независимы, а ошибка наблюдений – белый шум, то метод наименьших квадратов (МНК) позволяет получить несмещенные и эффективные оценки параметров в данной регрессии.
Несмещенность означает, что математическое ожидание полученных оценок совпадает с их истинным значениям.
Эффективность означает, что полученные случайные оценки имеют минимальную дисперсию.
Данную теорию обработки данных, т.е. выделения собственно значения показателя от скрадывающих его ошибок измерения Гаусс вывел для физических измерений.
На прямую теория ошибок наблюдения Гаусса не может применяться для экономических временных рядов по следующим причинам:
1. В экономике нет знаний как об истинном законе изменения показателей экономических процессов, так и об ошибках наблюдения.
2. Ряды наблюдений должны быть короткими. Чем ряд короче, тем он однороднее.
|
|
|
В Западной эконометрике в качестве аппроксимационных могут использоваться любые функции. Но экономические временные ряды как объект анализа обладают следующим замечательным свойством — у них нет преимущественного (естественного) начала отсчета времени. Именно по этой причине их изучение правомерно проводить в любой шкале времени t = to + 1, ..., to + N и руководствоваться единственно соображениями удобства, решая, чему положить to — нулю (что обычно и делается) или какому-либо другому числу. По этой причине для аппроксимации экономических временных рядов подходят только инвариантные по сдвигу аргумента функции.
Только три класса функций обладают этим свойством:
· Степенные полиномы
· Линейные комбинации показательных функций
· Линейные комбинации синуса и косинуса одинаковых частот
Любые линейные комбинации инвариантных функций также являются инвариантными функциями.
x(t)=  (t,
(t,  )+
)+ 
x(t), t= 
Инвариантность – независимость от сдвигов во времени.
Инвариантность функций обеспечивает лучшее качество моделей.
Ниже приведен пример экономического временного ряда x(t) и этот же ряд, сдвинутый по времени.
| t | x(t) | t | x(t)
| |||
| 1 | 2 | 9 | 2 | |||
| 2 | 3 | 10 | 3 | |||
| 3 | 4 | 11 | 4 | |||
| 4 | 6 | 12 | 6 | |||
| 5 | 8 | 13 | 8 | |||
| 6 | 10 | 14 | 10 | |||
| 7 | 12 | 15 | 12 | |||
| 11 | 19 |
Рассмотрим следующие три примера:
1.x(t)=a0+a1*√t
2.x(t)=a0+a1*lnt
3. x(t)=a0+a1*t
Произведем замену t  t+с
t+с
Тогда:
a0+a1*√t+с ≠ 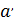 0+
0+ 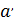 1*√t – неинвариантна
1*√t – неинвариантна
Пример 1
x(t)=a0+a1*√t
| t | x(t) | x ̃ (t) | t | x(t) | x ̃ (t) |
| 1 | 2 | 0,71 | 9 | 2 | 1,14 |
| 2 | 3 | 3,27 | 10 | 3 | 3,04 |
| 3 | 4 | 5,23 | 11 | 4 | 4,84 |
| 4 | 6 | 6,89 | 12 | 6 | 6,57 |
| 5 | 8 | 8,35 | 13 | 8 | 8,23 |
| 6 | 10 | 9,67 | 14 | 10 | 9,82 |
| 7 | 12 | 10,88 | 15 | 12 | 11,36 |
| 11 |
| 15,024 | 19 |
| 17,05 |
Решение:
Задача решается в отношении неизвестных a0 и a1 .
а) min ∑7t=1 [a0 + a1√t – x(t)]2
сумма квадратичных отклонений (мера близости временного ряда)
Обозначим ∑7t=1 [a0 + a1√t – x(t)]2=f(a0, a1)
Тогда уравнения в нормальной форме будут иметь вид:
 ∂F/∂a0 = 2 ∑7t=1[a0 + a1√t – x(t)] 1 = 0
∂F/∂a0 = 2 ∑7t=1[a0 + a1√t – x(t)] 1 = 0
∂F/∂a1 = 2 ∑7t=1 [a0 + a1√t – x(t)] √t = 0
Уравнения в каноническом вида:
 (∑7t=11) a0 + (∑7t=1 √t) a1 = ∑7t=1 x(t)
(∑7t=11) a0 + (∑7t=1 √t) a1 = ∑7t=1 x(t)
|
|
|
(∑7t=1√t) a0 + (∑7t=1 t) a1 = ∑7t=1 x(t) √t
 7 a0 + 13,478 a1 = 45
7 a0 + 13,478 a1 = 45
13,478 a0 + 28 a1 = 99,303
Решая систему методом Крамера, получим

 7 13,478
7 13,478
∆ = = 14,344
13,478 28

 45 13,478
45 13,478
∆0 = = -78,406
99,303 28

 7 45
7 45
∆1 = = 88,611
13,478 99,303
a0 = ∆0 / ∆ = -5,466
a1 = ∆1 / ∆ = 6,178
Таким образом,
 = -5,466 + 6,178√t , для t=1,2,3,4,5,6,7,11
= -5,466 + 6,178√t , для t=1,2,3,4,5,6,7,11
б) Проводим аналогичные рассуждения для t=9,10,11,12,13,14,15,19
Уравнения в каноническом виде:
 7 a0 + 24,163 a1 = 45
7 a0 + 24,163 a1 = 45
24,163 a0 + 84 a1 = 162,275
Решая систему методом Крамера, получим:

 7 24,163
7 24,163
∆ = = 4,149
24,163 84

 45 24,163
45 24,163
∆0 = = -141,051
162,275 84

 7 45
7 45
∆1 = = 48,59
24,163 162,275
a0 = ∆0 / ∆ = -33,993
a1 = ∆1 / ∆ = 11,71
Таким образом,
 = -33,993 + 11,71√t , t = 9,10,11,12,13,14,15,19
= -33,993 + 11,71√t , t = 9,10,11,12,13,14,15,19
| t | x(t) | x ̃ (t) | t | x(t) | x ̃ (t) | ||
| 1 | 2 | 0,71 | 9 | 2 | 1,14 | ||
| 2
| 3 | 3,27 | 10 | 3 | 3,04 | ||
| 3 | 4 | 5,23 | 11 | 4 | 4,84 | ||
| 4 | 6 | 6,89 | 12 | 6 | 6,57 | ||
| 5 | 8 | 8,35 | 13 | 8 | 8,23 | ||
| 6 | 10 | 9,67 | 14 | 10 | 9,82 | ||
| 7 | 12 | 10,88 | 15 | 12 | 11,36 | ||
| 11 |
| 15,024 | 19 |
| 17,05 |
Пример 2
x(t)=a0+a1*lnt - неинвариантна
| t | x(t) | x ̃ (t) | t | x(t) | x ̃ (t) |
| 1 | 2 | 0,31 | 9 | 2 | 0,92 |
| 2 | 3 | 3,79 | 10 | 3 | 3,04 |
| 3 | 4 | 5,83 | 11 | 4 | 4,96 |
| 4 | 6 | 7,28 | 12 | 6 | 6,72 |
| 5 | 8 | 8,40 | 13 | 8 | 8,33 |
| 6 | 10 | 9,31 | 14 | 10 | 9,82 |
| 7 | 12 | 10,09 | 15 | 12 | 11,21 |
| 11 |
| 12,36 | 19 |
| 15,97 |
Решение:
Задача решается в отношении неизвестных a0 и a1 .
а) метод наименьших квадратов
min ∑7t=1 [a0 + a1lnt – x(t)]2
сумма квадратичных отклонений (мера близости временного ряда)
Обозначим ∑7t=1 [a0 + a1lnt – x(t)]2=f(a0, a1)
Тогда уравнения в нормальной форме будут иметь вид:
 ∂F/∂a0 = 2 ∑7t=1[a0 + a1lnt – x(t)] 1 = 0
∂F/∂a0 = 2 ∑7t=1[a0 + a1lnt – x(t)] 1 = 0
∂F/∂a1 = 2 ∑7t=1 [a0 + a1lnt – x(t)] lnt = 0
Уравнения в каноническом вида:
 (∑7t=11) a0 + (∑7t=1lnt) a1 = ∑7t=1 x(t)
(∑7t=11) a0 + (∑7t=1lnt) a1 = ∑7t=1 x(t)
(∑7t=1lnt) a0 + (∑7t=1 ln2t) a1 = ∑7t=1 x(t) lnt
Уравнения в каноническом виде:
 7 a0 + 8,525 a1 = 45
7 a0 + 8,525 a1 = 45
8,525 a0 + 13,196 a1 = 68.936
Решая систему методом Крамера, получим:

 7 8,525
7 8,525
∆ = = 19,696
8,525 13,196

 45 8,525
45 8,525
∆0 = = 6,141
68.936 13,196

 7 45
7 45
∆1 = = 98,927
8,525 68.936
a0 = ∆0 / ∆ = 0,312
a1 = ∆1 / ∆ = 5,023
Таким образом,
 = 0,312 + 5,023*lnt , для t=1,2,3,4,5,6,7,11
= 0,312 + 5,023*lnt , для t=1,2,3,4,5,6,7,11
б) Проводим аналогичные рассуждения для t=9,10,11,12,13,14,15,19
Уравнения в каноническом виде:
 7 a0 + 17,295 a1 = 45
7 a0 + 17,295 a1 = 45
17,295 a0 + 42,931 a1 = 115,21
Решая систему методом Крамера, получим:

 7 17,295
7 17,295
∆ = = 1,40
17,295 42,931

 45 17,295
45 17,295
∆0 = = -60,662
115,21 42,931

 7 45
7 45
∆1 = = 28,195
17,295 115,21
a0 = ∆0 / ∆ = -43,331
a1 = ∆1 / ∆ = 20,14
Таким образом,
 = -43,331 + 20,14*lnt, t = 9,10,11,12,13,14,15,19
= -43,331 + 20,14*lnt, t = 9,10,11,12,13,14,15,19
Пример 3
x(t)=a0+a1*t - инвариантна
| t | x(t) | x ̃ (t) | t | x(t) | x ̃ (t) |
| 1 | 2 | 1,29 | 9 | 2 | 1,28 |
| 2 | 3 | 3,00 | 10 | 3 | 3,00 |
| 3 | 4 | 4,71 | 11 | 4 | 4,71 |
| 4 | 6 | 6,43 | 12 | 6 | 6,43 |
| 5 | 8 | 8,14 | 13 | 8 | 8,14 |
| 6 | 10 | 9,86 | 14 | 10 | 9,85 |
| 7 | 12 | 11,57 | 15 | 12 | 11,57 |
| 11 |
| 18,43 | 19 |
| 18,42 |
Решение:
Задача решается в отношении неизвестных a0 и a1 .
а) метод наименьших квадратов
min ∑7t=1 [a0 + a1t – x(t)]2
сумма квадратичных отклонений (мера близости временного ряда)
Обозначим ∑7t=1 [a0 + a1t – x(t)]2=f(a0, a1)
Тогда уравнения в нормальной форме будут иметь вид:
 ∂F/∂a0 = 2 ∑7t=1[a0 + a1t – x(t)] 1 = 0
∂F/∂a0 = 2 ∑7t=1[a0 + a1t – x(t)] 1 = 0
∂F/∂a1 = 2 ∑7t=1 [a0 + a1t – x(t)] t = 0
Уравнения в каноническом вида:
 (∑7t=11) a0 + (∑7t=1 t) a1 = ∑7t=1 x(t)
(∑7t=11) a0 + (∑7t=1 t) a1 = ∑7t=1 x(t)
(∑7t=1t) a0 + (∑7t=1 t2) a1 = ∑7t=1 x(t) t
Уравнения в каноническом виде:
 7 a0 + 28 a1 = 45
7 a0 + 28 a1 = 45
28 a0 + 140 a1 = 228
Решая систему методом Крамера, получим:

 7 28
7 28
∆ = = 196
28 140

 45 28
45 28
∆0 = = -84
228 140

 7 45
7 45
∆1 = = 336
28 228
a0 = ∆0 / ∆ = -0,429
a1 = ∆1 / ∆ = 1,714
Таким образом,
 = -0,429 + 1,714t , для t=1,2,3,4,5,6,7,11
= -0,429 + 1,714t , для t=1,2,3,4,5,6,7,11
б) Проводим аналогичные рассуждения для t=9,10,11,12,13,14,15,19
Уравнения в каноническом виде:
 7 a0 + 84 a1 = 45
7 a0 + 84 a1 = 45
84 a0 + 1036 a1 = 588
Решая систему методом Крамера, получим:

 7 84
7 84
∆ = = 196
84 1036

 45 84
45 84
∆0 = = -2772
588 1036

 7 45
7 45
∆1 = = 336
84 588
a0 = ∆0 / ∆ = -14,043
a1 = ∆1 / ∆ = 1,714
Таким образом,
 = -14,043 + 1,714t , t = 9,10,11,12,13,14,15,19
= -14,043 + 1,714t , t = 9,10,11,12,13,14,15,19
Вывод: только в третьем примере результаты остались прежними при вычислении на другом интервале времени, то есть примеры наглядно демонстрируют, что неинвариантные по сдвигу аргумента функции приводят к разным результатам в зависимости от выбранного начала отчета.
Метод компромисса «точность-надежность» в анализе экономических временных рядов.
Имеется исходный временной ряд X(t), t=1…N
Необходимо построить наиболее точную и надежную функцию регрессии выбранного вида:
Xt=a0+a1t+….+altl+ δt
То есть нужно ai и l.
В качестве аппроксимирующих функций рассматриваются только функции определенного вида (степенные полиномы). Временной ряд разбивается на полином и невязки и невязки:
X(t)=Pl(t)+ δl(t)
Критерий компромисса «точность-надежность»:
В качестве наилучшей по компромиссу «точность-надежность» в экономической линейной полиномиальной модели мы выбираем наиболее точную из допустимых по надежности оценок старших коэффициентов полинома.
Пример
Пусть имеется временной ряд капитальных вложений: x(t)
Построить наилучшую регрессионную модель для ряда инвестиций.
| t | x(t) | P1(t) | δ1(t) | P2(t) | δ2(t) | P3(t) | δ3(t) |
| 1 | 10,8 | 6,91 | 3,89 | 10,324 | 0,476 | 9,829 | 0,971 |
| 2 | 12,1 | 9,56 | 2,54 | 11,897 | 0,203 | 11,714 | 0,386 |
| 3 | 12,7 | 12,21 | 0,49 | 13,589 | -0,889 | 13,632 | -0,932 |
| 4 | 15 | 14,86 | 0,14 | 15,401 | -0,401 | 15,593 | -0,593 |
| 5 | 16,5 | 17,51 | -1,01 | 17,332 | -0,832 | 17,607 | -1,107 |
| 6 | 19,1 | 20,16 | -1,06 | 19,383 | -0,283 | 19,685 | -0,585 |
| 7 | 21,6 | 22,81 | -1,21 | 21,554 | 0,046 | 21,837 | -0,237 |
| 8 | 24,5 | 25,46 | -0,96 | 23,845 | 0,655 | 24,072 | 0,428 |
| 9 | 27,4 | 28,11 | -0,71 | 26,255 | 1,145 | 26,402 | 0,998 |
| 10 | 30,8 | 30,76 | 0,04 | 28,785 | 2,015 | 28,836 | 1,964 |
| 11 | 31,9 | 33,41 | -1,51 | 31,435 | 0,465 | 31,384 | 0,516 |
| 12 | 34 | 36,06 | -2,06 | 34,204 | -0,204 | 34,058 | -0,058 |
| 13 | 36,1 | 38,71 | -2,61 | 37,093 | -0,993 | 36,866 | -0,766 |
| 14 | 39,4 | 41,36 | -1,96 | 40,102 | -0,702 | 39,820 | -0,420 |
| 15 | 42,7 | 44,01 | -1,31 | 43,231 | -0,531 | 42,929 | -0,229 |
| 16 | 45,8 | 46,66 | -0,86 | 46,479 | -0,679 | 46,204 | -0,404 |
| 17 | 49,4 | 49,31 | 0,09 | 49,847 | -0,447 | 49,654 | -0,254 |
| 18 | 53,6 | 51,96 | 1,64 | 53,334 | 0,266 | 53,291 | 0,309 |
| 19 | 55,8 | 54,61 | 1,19 | 56,942 | -1,142 | 57,124 | -1,324 |
| 20 | 62,5 | 57,26 | 5,24 | 60,669 | 1,831 | 61,163 | 1,337 |
1. min ∑ 20t=1[a0 + a1 t – x(t)]2
 (∑20t=11) a0 + (∑20 t=1t) a1 = ∑20 t=1x(t)
(∑20t=11) a0 + (∑20 t=1t) a1 = ∑20 t=1x(t)
(∑20t=1t) a0 + (∑20 t=1t2) a1 = ∑20 t=1x(t) t
 20 a0 + 210 a1 = 641,7
20 a0 + 210 a1 = 641,7
210 a0 + 2870 a1 = 8499,9
Решаем это уравнение методом Крамера,

 20 210
20 210
∆ = = 13300
210 2870

 641,7 210
641,7 210
∆0 = = 56700
8499,9 2870

 20 641,7
20 641,7
∆1 = = 35241
210 8499,9
a0 = ∆0 / ∆ = 4,263
a1 = ∆1 / ∆ = 2,65
Таким образом:
P1(t) = 4,26 + 2,65 t , t = 1,20
δ1(t) = x(t) - P1(t) – невязка (разница между теоретическими и эксп. данными)
S2(1) = (∑ δ12(t)) / N = 78,083 / 20 = 3,90 – показатель точности приближения (средний квадрат ошибки модели)
Приводим исследование невязок на степень соответствия их свойств свойствам белого шума.
А) Динамика невязок

Число пересечений с осью времени мало. Таким образом, динамика невязок не дает оснований рассматривать невязки как практическую реализацию белого шума.
Б) Поле автокорреляции при l=1

В поле автокорреляции наблюдается тренд, что дает основания полагать, что автокорреляция есть. Следовательно, нельзя рассматривать ряд невязок как реализацию белого шума.
В) Численное значение автокорреляции:
∑δ1(t-1) δ1(t) 40,714

 r1(l) = = = 0,72 – высокая автокорреляция
r1(l) = = = 0,72 – высокая автокорреляция
√∑ δ12(t-1)∑ δ12(t) √50,625 * 62,951
Ошибка не белый шум, теоремой Гаусса – Маркова воспользоваться нельзя.
2. при l=2
min ∑ [a0 + a1 t + a2t2– x(t)]2
 ∂F/∂a0 = 2 ∑ [a0 + a1 t + a2t2 – x(t)] * 1 = 0
∂F/∂a0 = 2 ∑ [a0 + a1 t + a2t2 – x(t)] * 1 = 0
∂F/∂a1 = 2 ∑ [a0 + a1 t + a2t2 – x(t)] * t = 0
∂F/∂a2 = 2 ∑ [a0 + a1 t + a2t2 – x(t)] * t2 = 0
 (∑1) a0 + (∑t) a1 + (∑t2) a2 = ∑x(t)
(∑1) a0 + (∑t) a1 + (∑t2) a2 = ∑x(t)
(∑t) a0 + (∑t2) a1 +(∑t3) a2 = ∑x(t) t
(∑t2) a0 + (∑t3) a1 +(∑t4) a2 = ∑x(t) t2
 20 a0 + 210 a1 + 2870 a2 = 641,7
20 a0 + 210 a1 + 2870 a2 = 641,7
210 a0 + 2870 a1 + 44100 a2 = 8499,9
2870 a0 + 44100 a1 + 722666 a2 = 130137,7
Решаем систему методом Крамера

 20 210 2870
20 210 2870
∆ = 210 2870 44100 = 233494800
2870 44100 722666

 641,7 210 2870
641,7 210 2870
∆0 = 8499,9 2870 44100 = 2071447070
130137,7 44100 722666

 20 641,7 2870
20 641,7 2870
∆1 = 210 8499,9 44100 = 325230486
2870 130137,7 722666
Дата добавления: 2018-02-15; просмотров: 299; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
