Линейные дифференциальные уравнения
Дифференциальные уравнения 1-го порядка
Дифференциальные уравнения семейства кривых
Пусть задано семейство кривых:  , где
, где  - параметр. Необходимо составить дифференциальное уравнение, решением которого является это семейство.
- параметр. Необходимо составить дифференциальное уравнение, решением которого является это семейство.
Общая схема решения этой задачи:
1) Равенство  определяет неявную функцию
определяет неявную функцию  . Тогда на некотором промежутке справедливо тождество:
. Тогда на некотором промежутке справедливо тождество:  . Дифференцируя это тождество по переменной
. Дифференцируя это тождество по переменной  , получим:
, получим:  =
=  =
=  =0.
=0.
2) Запишем систему  Исключив параметр
Исключив параметр 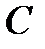 из этой системы, получим дифференциальное уравнение, решением которого является семейство кривых:
из этой системы, получим дифференциальное уравнение, решением которого является семейство кривых:  .
.
Пример 1.1. Имеем семейство кривых:  . Необходимо построить дифференциальное уравнение, для которого данное семейство кривых является решением.
. Необходимо построить дифференциальное уравнение, для которого данное семейство кривых является решением.
Решение: 1) Считая, что выражение 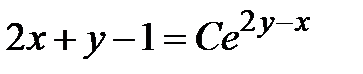 определяет неявную функцию
определяет неявную функцию  , продифференцируем это выражение по независимой переменной
, продифференцируем это выражение по независимой переменной  . Имеем
. Имеем  .
.
2) Запишем систему  Для исключения из системы параметра
Для исключения из системы параметра  умножим первое уравнение на
умножим первое уравнение на 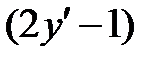 и приравняем левые части первого и второго равенств. Получим дифференциальное уравнение
и приравняем левые части первого и второго равенств. Получим дифференциальное уравнение  , или
, или  , решением которого является заданное семейство кривых.
, решением которого является заданное семейство кривых.
Ответ.  .
.
Задание 1.1. Составить дифференциальное уравнение для семейства кривых.
| Вар. | Семейство: | Вар. | Семейство: |
| 1.1.1. |  . .
| 1.1.16. |  . .
|
| 1.1.2. |  . .
| 1.1.17. |  . .
|
| 1.1.3. |  . .
| 1.1.18. |  . .
|
| 1.1.4. |  . .
| 1.1.19. |  . .
|
| 1.1.5. |  . .
| 1.1.20. |  . .
|
| 1.1.6. |  . .
| 1.1.21. | 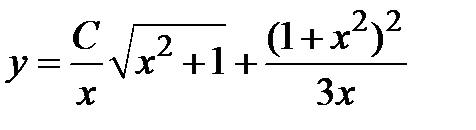 . .
|
| 1.1.7. |  . .
| 1.1.22. | 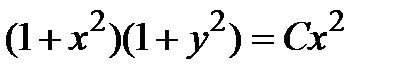 . .
|
| 1.1.8. |  . .
| 1.1.23. |  . .
|
| 1.1.9. | 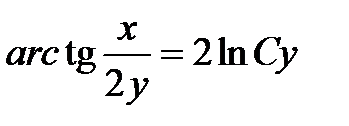 . .
| 1.1.24. |  . .
|
| 1.1.10. | 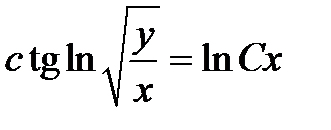 . .
| 1.1.25. |  . .
|
| 1.1.11. |  = =  . .
| 1.1.26. | 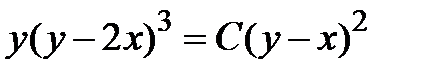 . .
|
| 1.1.12. |  . .
| 1.1.27. | 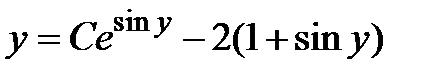 . .
|
| 1.1.13. |  . .
| 1.1.28. |  . .
|
| 1.1.14. |  . .
| 1.1.29. |  . .
|
| 1.1.15. |  . .
| 1.1.30. |  . .
|
Дифференциальные уравнения с разделяющимися переменными
|
|
|
Известно, что в общем случае дифференциальное уравнение с разделяющимися переменными может быть представлено в виде:
 . (1.1)
. (1.1)
Для интегрирования уравнения переменные  и
и  должны быть разделены. Для этого требуется разделить равенство (1.1) на произведение
должны быть разделены. Для этого требуется разделить равенство (1.1) на произведение  . В результате получим:
. В результате получим:
 . (1.2)
. (1.2)
Интегрируя (1.2), находим общее решение исходного уравнения (1.1) в виде выражения:  .
.
Для перехода к записи (1.2) выполнялось деление на функции: 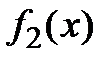 и
и  . Если возможны равенства
. Если возможны равенства  и
и  , необходимо функции
, необходимо функции  и
и  учесть как решения исходного уравнения.
учесть как решения исходного уравнения.
Пример 1.2. Решить дифференциальное уравнение  .
.
Решение. 1) Заданное уравнение есть уравнение с разделяющимися переменными, где  и
и  . Так как
. Так как  и
и  , то функции
, то функции  и
и  необходимо учесть как решения исходного уравнения.
необходимо учесть как решения исходного уравнения.
|
|
|
2) Теперь считаем, что 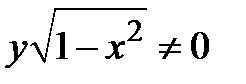 . Разделив заданное уравнение на
. Разделив заданное уравнение на  , получим уравнение
, получим уравнение  с разделенными переменными.
с разделенными переменными.
3) В результате интегрирования находим общее решение уравнения в виде  или
или  . Учитывая, что
. Учитывая, что  − произвольная постоянная величина, запишем общее решение в виде
− произвольная постоянная величина, запишем общее решение в виде  . При
. При  =0 из общего решения получаем также решение
=0 из общего решения получаем также решение  .
.
Ответ.  ;
;  .
.
Задание 1.2. Решить уравнение с разделяющимися переменными.
| Вар. | Уравнение: | Вар. | Уравнение: |
| 1.2.1. | 
| 1.2.16. | 
|
| 1.2.2. | 
| 1.2.17. | 
|
| 1.2.3. | 
| 1.2.18. | 
|
| 1.2.4. | 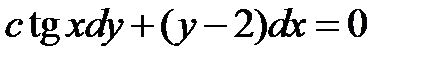
| 1.2.19. | 
|
| 1.2.5. | 
| 1.2.20. | 
|
| 1.2.6. | 
| 1.2.21. | 
|
| 1.2.7. | 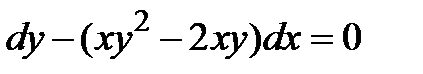
| 1.2.22. | 
|
| 1.2.8. | 
| 1.2.23. | 
|
| 1.2.9. | 
| 1.2.24. | 
|
| 1.2.10. | 
| 1.2.25. | 
|
| 1.2.11. | 
| 1.2.26. | 
|
| 1.2.12. | 
| 1.2.27. | 
|
| 1.2.13. | 
| 1.2.28. | 
|
| 1.2.14. | 
| 1.2.29. | 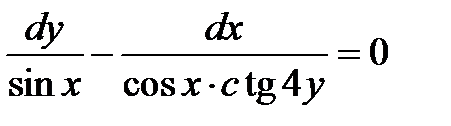
|
| 1.2.15. | 
| 1.2.30. | 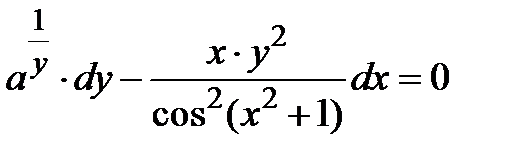
|
Однородные дифференциальные уравнения
В общем случае однородное дифференциальное уравнение может быть представлено в виде:
 , (1.3)
, (1.3)
где функции  и
и  однородные функции одного порядка. Используя свойства однородных функций, уравнение (1.3) можно переписать в виде
однородные функции одного порядка. Используя свойства однородных функций, уравнение (1.3) можно переписать в виде  .
.
Однородное уравнение решают с использованием замены  , то есть
, то есть 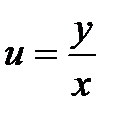 . Вычислим
. Вычислим  . Подставим
. Подставим  и
и  в уравнение (1.3):
в уравнение (1.3):
|
|
|
 . (1.4)
. (1.4)
Так как уравнение (1.4) есть уравнение с разделяющимися переменными  и
и  , то остается применить общий алгоритм решения дифференциальных уравнений с разделяющимися переменными, как в разделе (1.2). Решив уравнение (1.4) с помощью замены
, то остается применить общий алгоритм решения дифференциальных уравнений с разделяющимися переменными, как в разделе (1.2). Решив уравнение (1.4) с помощью замены  , записываем решение исходного уравнения (1.3).
, записываем решение исходного уравнения (1.3).
Пример 1.3. Решить дифференциальное уравнение  .
.
Решение. 1) Легко заметить, что в нашем случае  =
=  и
и  =
=  − однородные функции 2-го порядка, которое решаем применением замены
− однородные функции 2-го порядка, которое решаем применением замены  , то есть
, то есть  .
.
2) Используя  , перепишем уравнение
, перепишем уравнение  – уравнение с разделяющимися переменными
– уравнение с разделяющимися переменными  и
и  . Для полученного уравнения выделим очевидные решения
. Для полученного уравнения выделим очевидные решения  =0, то есть
=0, то есть  и
и  .
.
3) После этого запишем уравнение в виде  =
=  , которое легко интегрируется
, которое легко интегрируется  =
=  , или
, или 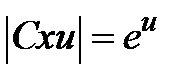 , или
, или  . Учитывая, что
. Учитывая, что  − произвольная постоянная величина, запишем общее решение в виде
− произвольная постоянная величина, запишем общее решение в виде  .
.
4) Учитывая что  , запишем общее решение уравнения
, запишем общее решение уравнения  . При
. При  =0 из общего решения получаем также решение
=0 из общего решения получаем также решение  .
.
Ответ.  ;
;  =0.
=0.
Задание 1.3. Решить однородное уравнение.
| Вар. | Уравнение: | Вар. | Уравнение: |
| 1.3.1. | 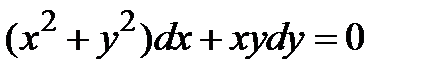
| 1.3.16. | 
|
| 1.3.2. | 
| 1.3.17. | 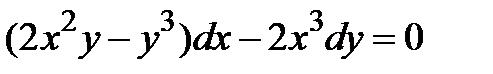
|
| 1.3.3. | 
| 1.3.18. | 
|
| 1.3.4. | 
| 1.3.19. | 
|
| 1.3.5. | 
| 1.3.20. | 
|
| 1.3.6. | 
| 1.3.21. | 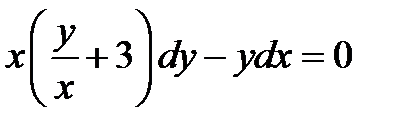
|
| 1.3.7. | 
| 1.3.22. | 
|
| 1.3.8. | 
| 1.3.23. | 
|
| 1.3.9. | 
| 1.3.24. | 
|
| 1.3.10. | 
| 1.3.25. | 
|
| 1.3.11. | 
| 1.3.26. | 
|
| 1.3.12. | 
| 1.3.27. | 
|
| 1.3.13. | 
| 1.3.28. | 
|
| 1.3.14. | 
| 1.3.29. | 
|
| 1.3.15. | 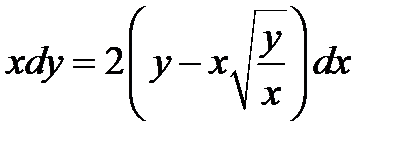
| 1.3.30. | 
|
Линейные дифференциальные уравнения
|
|
|
Заданное дифференциальное уравнение называют линейным, если искомая функция и ее производная входят в уравнение в 1-ой степени:
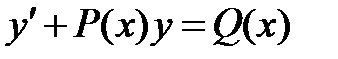 .
.
Рассмотрим решение уравнения, записанного в виде  применением подстановки (метод Бернулли)
применением подстановки (метод Бернулли)  , где
, где  и
и  .
.
Для функции  вычислим производную
вычислим производную  и вместе с выражением
и вместе с выражением  подставим в заданное уравнение:
подставим в заданное уравнение:
 . (1.5)
. (1.5)
Потребуем, чтобы функция  удовлетворяла условию
удовлетворяла условию  . Это уравнение с разделяющимися переменными. Нам нужно одно частное решение уравнения. Разделим переменные и проинтегрируем
. Это уравнение с разделяющимися переменными. Нам нужно одно частное решение уравнения. Разделим переменные и проинтегрируем  , или
, или  . Подставив
. Подставив  в (1.5), получим для нахождения
в (1.5), получим для нахождения  уравнение с разделяющимися переменными
уравнение с разделяющимися переменными  . Последнее легко интегрируется
. Последнее легко интегрируется  +
+  .
.
Остаётся записать общее решение заданного уравнения 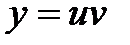 =
= 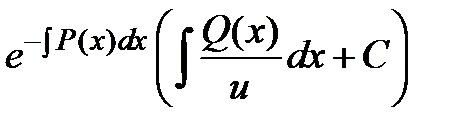 , из которого для заданных начальных условий
, из которого для заданных начальных условий  выделяют частное решение.
выделяют частное решение.
Пример 1.4. Решить дифференциальное уравнение  . Найти его частное решение при условии
. Найти его частное решение при условии  .
.
Решение. 1) Заданное уравнение линейное относительно  и
и  , причём
, причём  и
и  .
.
2) Применяя подстановку  , перепишем заданное уравнение
, перепишем заданное уравнение 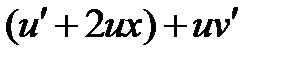 =
=  .
.
3) Потребуем, чтобы  . Это уравнение с разделяющимися переменными. Его частное решение
. Это уравнение с разделяющимися переменными. Его частное решение 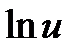 =
=  , или
, или 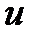 =
=  .
.
4) Теперь, интегрируя уравнение:  , получаем
, получаем  =
=  +
+  =
=  +
+  .
.
5) Записываем общее решение заданного уравнения  =
=  ·
·  .
.
6) Используя начальные условия (задача Коши), находим  =1 и записываем частное решение уравнения
=1 и записываем частное решение уравнения  =
=  ·
·  .
.
Ответ.  =
= 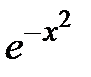 ·
·  – общее решение,
– общее решение,  =
=  ·
·  – частное решение.
– частное решение.
Задание 1.4. Решить линейное дифференциальное уравнение и найти частное решение для заданных начальных условий.
Дата добавления: 2018-02-15; просмотров: 817; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
