Собственные векторы и собственные значения линейного оператора

Линейные операторы

Линейный оператор. Ядро и образ линейного оператора

В линейной алгебре часто рассматриваются соответствия, при которых векторам одного линейного пространства ставят в соответствие векторы другого (или того же) линейного пространства.

Определение 5.1. Пусть заданы два линейных пространства . Если каждому вектору поставлен в соответствие единственный вектор

то говорят, что в пространстве задано отображение (функция)

При этом вектор называют прообразом вектора , а вектор – образом вектора . Линейные пространства называются соответственно пространством прообразов и пространством образов.

Частным случаем отображения линейных пространств является отображение пространства на себя:

Определение 5.2. Отображение , переводящее линейное пространство V в себя, называется линейным оператором (или линейным преобразованием), действующим в V, если для любых векторов и любого числа :

1) (аддитивность),

2) (однородность).

При этом запись , или называют операторной записью (или операторным равенством).

Условия 1), 2) определения 5.2 можно скомбинировать в виде одного: для любых векторов и любых чисел :

Отметим ряд свойств линейного оператора, непосредственно следующих из определения 5.2.

Теорема 5.1(об образе нулевого вектора). Линейный оператор переводит нулевой вектор в нулевой вектор.

□ Имеем . ■

Приведенное свойство может рассматриваться как необходимое (но не достаточное) условие линейности оператора. Если данное свойство не выполняется для данного отображения, то это отображение не является линейным оператором.

Теорема 5.2(об образе линейной комбинации). При линейном преобразовании образ линейной комбинации равен линейной комбинации образов, то есть если задана система векторов , то

Доказательство следует непосредственно из определения 5.2.

Теорема 5.3. Если система векторов линейно зависима, то система образов также линейно зависима.

□ Если система векторов линейно зависима, то существуют числа , среди которых есть хотя бы одно отличное от нуля, что

, .

Тогда, действуя оператором на обе части этого равенства (используя теоремы 5.1 и 5.2), получим

, ,

откуда следует линейная зависимость системы . ■

Теорема 5.4 (об однозначном задании линейного оператора).Линейный оператор, действующий в конечномерном линейном пространстве, однозначно задается образами базисных векторов этого линейного пространства.

□ Пусть – фиксированный базис в конечномерном линейном пространстве ( ). Выберем произвольную систему векторов . Покажем, что существует единственный линейный оператор , переводящий вектор в соответствующий вектор : .

Рассмотрим отображение , которое каждому вектору , имеющему в базисе разложение

ставит в соответствие вектор по правилу

При всех : .

Покажем, что введенное отображение является аддитивным и однородным. Для любых векторов , и любого числа :

Существование линейного оператора доказано. Единственность доказывается методом от противного. ■

Определение 5.3. Ядром линейного оператора называется множество векторов таких, что :

Из определения видно, что ядром линейного оператора являются те векторы пространства , которые переводятся оператором в нулевой вектор этого пространства.

Определение 5.4. Образом линейного оператора называется множество всех векторов для каждого :

Теорема 5.5.Ядро и образ линейного оператора, действующего в линейном пространстве, являются подпространствами линейного пространства.

□ Для доказательства теоремы достаточно показать, что множества и образ непустые и замкнуты относительно операций сложения векторов и умножения вектора на число.

Очевидно, что ядро является непустым, так как по теореме 5.1 образом нулевого вектора является нулевой вектор , то есть . Аналогично .

Покажем далее, что множество замкнуто относительно операций сложения векторов и умножения вектора на число, то есть покажем, что если , то при всех : . Имеем

то есть .

Аналогично показывается, что множество замкнуто относительно операций сложения векторов и умножения вектора на число. ■

Поскольку по теореме 5.5 ядро и образ являются подпространствами линейного пространства, то можно говорить об их размерностях.

Определение 5.5. Дефектом линейного оператора называют размерность ядра этого оператора. Рангом линейного оператора называют размерность образа линейного оператора. Итак,

, .

Справедлива следующая теорема о дефекте и ранге линейного оператора.

Теорема 5.6 (о размерностях ядра и образа линейного оператора).Сумма дефекта и ранга линейного оператора, действующего в конечномерном линейном пространстве, равна размерности этого линейного пространства:

Доказательство. Пусть , . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства. Покажем, что векторы

образуют базис подпространства , то есть покажем, что эта система векторов линейно независима и любой вектор может быть представлен в виде линейной комбинации векторов . Если и , то

Равенство

означает, что вектор представлен в виде линейной комбинации векторов .

Покажем теперь, что система векторов линейно независима. Составим равенство

и покажем, что оно выполняется только в случае, когда .

Так как линейный оператор, то по теореме 5.2

Из последнего равенства следует, что вектор

Покажем, что

Отметим, что векторы порождают некоторое подпространство , являющееся линейной оболочкой этих векторов[1]: .

Покажем, что подпространства и пересекаются только по нулевому вектору. Действительно, пусть . Тогда имеют место разложения вектора по векторам базисов этих двух подпространств:

Вычитая из первого равенства второе, получим

Так как система векторов является базисом пространства (а значит, она линейно независима), то последнее равенство возможно только в том случае, когда 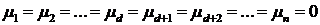. Это означает, что .

Выше было показано, что . Но . Значит, . Так как система векторов является линейно независимой, то последнее равенство возможно только в том случае, когда

Итак, система векторов образует базис подпространства , а значит, , что и доказывает справедливость утверждения теоремы. ■

Матрица линейного оператора

В силу теоремы 5.4 линейный оператор в конечномерном линейном пространстве однозначно можно задать при помощи образов базисных векторов. Наряду с ядром, образом, дефектом и рангом для линейного оператора имеет место такая характеристика, как матрица этого оператора.

Пусть – базис в конечномерном линейном пространстве ( ). Тогда по теореме 5.4 для любых векторов существует единственный линейный оператор , переводящий векторы базиса в соответствующие векторы , что можно записать в виде следующей операторной системы:

Разложим векторы через векторы базиса :

где – некоторые числа.

Определение 5.6.Квадратная матрица

столбцами которой являются координатные вектор-столбцы векторов в базисе , называется матрицей линейного оператора в базисе .

Следующая теорема позволяет найти координаты образа в базисе через матрицу оператора и координаты прообраза в том же базисе.

Теорема 5.7. Пусть линейный оператор, действующий в линейном пространстве и базис в . Тогда вектор-столбец координат вектора равен произведению

(5.1)

матрицы оператора в данном базисе на вектор-столбец координат вектора в данном базисе.

□ Пусть в базисе линейный оператор имеет матрицу . Разложим векторы через базисные векторы

Учитывая, что образы базисных векторов базиса имеют разложения

получим

В силу того, что разложение вектора по базису единственно, получим

что равносильно матричному равенству (5.1). ■

Матрица линейного оператора изменяется, когда изменяется базис линейного пространства. Найдем связь между матрицами линейного оператора в разных базисах этого линейного пространства.

Теорема 5.8 (о связи матриц линейного оператора в разных базисах). Пусть , – базисы в линейном пространстве . Матрицы и оператора в базисах , связаны равенством

, (5.2)

где – матрица перехода от базиса к базису .

□ Пусть вектору в базисах , соответствуют вектор-столбцы , а вектору вектор-столбцы . Тогда в силу матричного равенства (5.1), имеем

где матрицы линейного оператора в базисах , .

Далее, если есть матрица перехода от к , то используя формулы преобразования координат при переходе от базиса к базису, получим

откуда и следует справедливость равенства (5.2). ■

Теорема 5.9.Определитель матрицы линейного оператора не зависит от выбора базиса.

□ Пусть оператор в базисах , имеет соответствующие матрицы . Тогда на основании равенства (5.2) и свойств определителей имеем

■

Согласно теореме 5.9 при смене базиса линейного пространства изменяется матрица оператора, а определитель её при этом остается неизменным. Значит, этот определитель характеризует не конкретную матрицу оператора в данном базисе, а сам оператор. Это позволяет ввести следующее определение.

Определение 5.7.Определителем линейного оператора, действующего в линейном пространстве, называется определитель матрицы этого оператора в любом базисе.

Теорема 5.10.Ранг линейного оператора совпадает с рангом матрицы этого оператора.

Пример 5.1.Записать матрицу линейного оператора , заданного по правилу

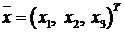
в базисе , где .

Найти образ, ранг, ядро, дефект, базисы образа и ядра оператора.

Решение. Находим образы векторов :

Для составления матрицы линейного оператора в базисе найдем коэффициенты разложения векторов через базисные векторы . Для этого необходимо решить систему уравнений (см. определение матрицы линейного оператора)

Каждое из уравнений этой системы решаем отдельно. Первое уравнение можно переписать в виде

Решая его, получим вектор-столбец координат вектора в базисе :

Решая аналогично остальные два уравнения, получим координатные вектор-столбцы векторов в базисе :

, .

В результате матрица линейного оператора в базисе имеет вид

Для нахождения ядра линейного оператора необходимо решить однородную систему уравнений с матрицей . Находя ее общее решение, получим ядро оператора, каждый вектор которого имеет вид

Очевидно, что размерность ядра (дефект оператора) равна

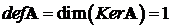базисный вектор в ядре – вектор-столбец

Размерность образа оператора (ранг оператора) равна

Для нахождения базиса образа исследуем на линейную зависимость систему векторов и найдем максимальную систему линейно независимых векторов. Составим матрицу и приведём ее к ступенчатому виду (в результате элементарных преобразований нумерация столбцов не изменялась):

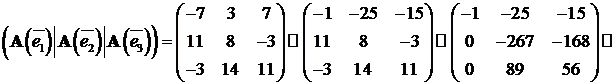
Из вида ступенчатой матрицы следует, что базис образа образуют векторы .

Собственные векторы и собственные значения линейного оператора

Важнейшими характеристиками линейного оператора являются его собственные векторы и собственные значения.

Пусть в линейном пространстве задан линейный оператор .

Определение 5.8. Ненулевой вектор ( ), удовлетворяющий условию (операторному равенству)

, , (5.3)

называется собственным вектором оператора . Число при этом называется собственным значением (собственным числом) оператора , соответствующим собственному вектору .

Определение 5.9. Множество 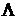всех собственных значений оператора называется спектром линейного оператора.

Выберем в пространстве некоторый базис , и пусть оператору в этом базисе соответствует матрица . Тогда операторное равенство (5.3) можно переписать в матричном виде

, ,

или в виде системы уравнений

(5.4)

Так как нас интересуют нетривиальные решения системы (5.4) (поскольку собственный вектор по определению должен быть ненулевым), то основная матрица 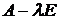системы (5.4) должна быть вырожденной, то есть

Определение 5.10. Уравнение

(5.5)

называется характеристическим уравнением линейного оператора .

Разложив определитель в уравнении (5.5), получим многочлен

(5.6)

-ой степени относительно . Многочлен (5.6) называется характеристическим многочленом оператора , его корни – характеристическими корнями многочлена (5.6).

Теорема 5.11.Характеристическое уравнение (5.5) оператора не зависит от выбора базиса.

□ Теорема утверждает, что если в пространстве выбраны два различных базиса, то характеристическое уравнение оператора будет иметь один и тот же вид. Пусть оператору в базисах и соответствуют матрицы . Тогда, если матрица перехода от базиса к базису , то

Итак, имеем

что и означает, что характеристическое уравнение оператора не зависит от выбора базиса. ■

Согласно теореме 5.11, характеристический многочлен (5.6) и его корни не зависят от выбора базиса, а значит, определение 5.10 введено корректно. При этом характеристическое уравнение и характеристический многочлен являются инвариантами линейного оператора относительно выбора базиса (они являются характеристиками самого оператора, а не его матрицы в конкретном базисе).

Каждому собственному значению линейного оператора соответствуют свои собственные векторы, причем таких векторов бесконечно много. То есть, если есть собственный вектор линейного оператора , то вектор , где , также есть собственный вектор оператора :

Теорема 5.12.Для того чтобы число являлось собственным значением линейного оператора , необходимо и достаточно, чтобы оно было корнем характеристического уравнения (5.5) этого оператора.

Определение 5.11. Алгебраической кратностью собственного значения линейного оператора называется кратность корня характеристического уравнения (5.5) (кратность корня характеристического многочлена ). Кратностью корня называется натуральное число такое, что

, , …, , .

Определение 5.12. Спектр 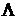линейного оператора называется простым, если алгебраическая кратность каждого собственного значения равна единице. Спектр 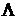линейного оператора называется сложным, если среди собственных значений оператора имеется хотя бы одно, алгебраическая кратность которого больше единицы.

Дата добавления: 2018-02-15; просмотров: 510; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!