Эквивалентность процентных ставок различного типа
Эквивалентные процентные ставки - это такие процентные ставки разного вида, применение которых при различных начальных условиях дает одинаковые финансовые результаты.
Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок.
Для нахождения эквивалентных процентных ставок используют уравнения эквивалентности, принцип составления которых заключается в следующем. Выбирается величина, которую можно рассчитать при использовании различных процентных ставок (обычно это наращенная сумма S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.
Повторим формулы для определения наращенной суммы при различных способах начисления процентов:
; 
; 
; 
; 
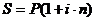Приравнивая эти формулы попарно, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.
Рассмотрим несколько случаев.
1) 
, откуда 
; 
.
2) 
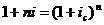, откуда 
; 
.
3) 
, откуда 
; 
Для различных случаев сложных процентов получаем следующее уравнение эквивалентности:
|
|
|
4) 
, откуда 
; 
.
Полученная по последней формуле годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной (действительной) ставкой сложных процентов.
Эффективную ставку сложных процентов полезно знать, чтобы оценить реальную доходность финансовой операции, или сравнить процентные ставки в случае, когда используются различные интервалы начисления.
Далее для установления эквивалентности между сложными учетными ставками и сложными ставками ссудных процентов имеем:
5) 
, откуда 
; 
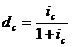
Аналогичным образом получаем зависимости между любыми другими эквивалентными процентными ставками.
Учет инфляционного обесценения денег в принятии финансовых решений.
Пусть Sa- сумма, покупательная способность которой с учетом инфляции равна покупательной способности суммы S при отсутствии инфляции. Через 
обозначим разницу между этими суммами.
Отношение / S, выраженное в процентах, называется уровнем инфляции.
При расчетах используют относительную величину уровня инфляции - темп инфляции 
.
, отсюда 
Тогда для определения Sa получаем следующее выражение:
.
|
|
|
Величину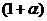 
, показывающую, во сколько раз Sa больше S (т. е. во сколько раз в среднем выросли цены), называют индексом инфляции 
.
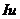Динамика индекса инфляции за несколько лет отражает изменения, происходящие в инфляционных процессах. Понятно, что повышение индекса инфляции за определенный период по сравнению с предыдущим таким же периодом указывает на ускорение инфляции, снижение - на уменьшение ее темпов.
Пусть - годовой уровень инфляции. Через п лет сумма S: вырастет по отношению к сумме S в 
раз.
Разумеется, те же рассуждения применяются, если вместо года берется любой другой временной интервал (квартал, месяц, день и т. д.).
Рассмотрим теперь различные случаи задания уровня инфляции.
Если известен годовой уровень инфляции , то за период в п лет (при том, чтo 
и 
- целое число лет, 
- оставшаяся нецелая часть года) индекс инфляции, очевидно, составит следующую величину: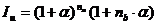 
В некоторых случаях может быть задан уровень инфляции 
за короткий (меньше года) интервал. Тогда за период, составляющий т таких интервалов, индекс инфляции будет равен: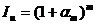 
Теперь можно приложить изложенные выше варианты начисления процентов к условиям инфляционной экономики.
Если в обычном случае первоначальная сумма Р при заданной ставке процентов превращается за определенный период в сумму S, то в условиях инфляции она должна превратиться в сумму 
, что требует уже иной процентной ставки.
|
|
|
Назовем ее ставкой процентов, - учитывающей инфляцию.
Пусть:
- простая ставка ссудного процента, учитывающая инфляцию;
- сложная ставка ссудного процента, учитывающая инфляцию;
- простая учетная ставка, учитывающая инфляцию;
- сложная учетная ставка, учитывающая инфляцию;
номинальная ставка сложного процента, учитывающая инфляцию (с использование интервалов начисления);
- номинальная сложная учетная ставка, учитывающая инфляцию (с использование интервалов начисления).
Зададим годовой уровень инфляции и простую годовую ставку ссудного процента i. Тогда для наращенной суммы S, превращающейся в условиях инфляции в сумму , используем формулу: 
.
Для данной суммы можно записать еще одно соотношение: 
а затем составить уравнение эквивалентности: 
из которого следует, что 
Мы получили, таким образом, известную формулу И. Фишера, в которой сумма 
является величиной, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь эта величина называется инфляционной премией.
|
|
|
Рассмотрим теперь различные случаи начисления процентов с учетом инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период.
Для простых процентных ставок получаем: 
в то же время должно выполняться равенство: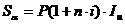 
Составим уравнение эквивалентности: 
из которого получаем:
Для простых учетных ставок аналогичное уравнение эквивалентности будет иметь вид:
, откуда
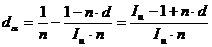
Для случая сложных процентов используем формулы: 
и 
Отсюда 
Если начисление процентов происходит несколько (m) раз в году, используется следующая формула:
,
Отсюда
Таким же образом получаем две формулы для случаев сложных учетных ставок:
Используя полученные Формулы, можно находить процентную ставку, компенсирующую потери от инфляции, когда заданы процентная ставка, обеспечивающая желаемую доходность финансовой операции, и уровень инфляции в течение рассматриваемого периода. Эти формулы можно преобразоватъ и получить зависимость i от или любую другую. Например, из формулы можно получить формулу, позволяющую определить реальную доходность финансовой операции, когда задан уровень инфляции и простая ставка процентов, учитывающая инфляцию: 
Из Формулы - получаем аналогичную формулу для случая сложных процентов: 
Подставив в последнюю формулу вместо индекса инфляции выражение 
, получим простую формулу: 
, отражающую несколько очевидных соображений:
если 
(доходность вложений и уровень инфляции равны), то 
, т. е. весь доход поглощается инфляцией;
если 
(доходность вложений ниже уровня инфляции), то 
, то есть операция приносит убыток;
если 
(доходность вложений выше уровня инфляции), то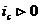 
, т.е. происходит реальный прирост вложенного капитала.
Дата добавления: 2018-02-15; просмотров: 1854; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!