Метод аппроксимации частотных характеристик с помощью многочленов Чебышева.
Имеется несколько методов расчётов импульсных характеристик, а именно: · Оконный метод · Метод аппроксимации частотных характеристик с помощью многочленов Чебышева · Метод линейного программирования Оконный метод (метод взвешивания) самый простой метод. В принципе, если - задано, то: Тогда: (1) Использование обратного преобразования Фурье позволяет вычислить импульсную характеристику, но бесконечной длины. Импульсная характеристика имеет бесконечную длину, поскольку суммирование производится в бесконечных пределах. Желаемая частотная характеристика может быть воспроизведена в точности только тогда, когда импульсная характеристика бесконечной длины. Лучшие результаты даёт метод проектирования КИХ – фильтров, с помощью весовой последовательности конечной длины, называемой окном. Эта последовательность используется для модификации коэффициентов Фурье с тем, чтобы управлять сходимостью ряда Фурье. В реальности предполагается использовать только первое N+1 значение импульсной характеристики. Легко показать, что эта частотная характеристика будет связана с желаемой частотной характеристикой следующим образом. Подставим в определение КИХ выражение (87): Геометрическая прогрессия: Так, что: (2) (3) АЧХ – Амплитудно- Частотная Характеристика весовой функции вида: (4) Окном анализа принято называть некоторую функцию отсчётов, которая равна нулю вне интервала от 0 до N и изменяется по некоторому закону там, где она принимает ненулевые значения. Законы изменения значений оконной функции могут быть различны, однако, основным требованием к ним является мера узости в частотной области. Для каждого вида окна можно вычислить ей частотную характеристику: Для большинства приемлемых окон функция имеет главный лепесток, содержащий почти всю энергию окна, и боковые лепестки, которые обычно быстро затухают. Если есть набор: То оконная обработка предполагает, что: Трансформанта Фурье, это будет: (5) Частотная характеристика прямоугольного окна: Максимум, когда числитель равен 1. Прямоугольное окно критикуется за то, что у него большие боковые лепестки, которые искажают, за счёт интервала свёртки, частотную характеристику фильтра. Желательно, чтобы окно обладало следующими свойствами: 1) Ширина главного лепестка частотной характеристики окна, содержащего по возможности большую часть общей энергии, должна быть малой. Расширение главного лепестка соответствует расширению переходной полосы между полосами пропускания и непропускания 2) Энергия в боковых лепестках частотной характеристики окна должна быстро уменьшаться при приближении к . Уменьшение уровня боковых лепестков соответствует меньшим пульсациями в полосе пропускания и лучшему подавлению в полосе непропускания фильтра. Чтобы уменьшить влияние боковых лепестков придумали различные виды окон: a) Треугольное (окно Бартлетта) b) Косинус – квадрат (окно Ханна) c) Приподнятый косинус (окно Хэмминга)
|
|
|
|
|
|
Окно Бартлетта.


У окна Бартлетта основной лепесток будет в два раза шире, но боковые меньше.
Все окна, которые известны, приводят к расширению основного лепестка за счёт уменьшения амплитуды боковых. Это достигается за счёт того, что окна по краям имеют значения близкие к нулю.
Окно Ханна.
Исторически потом было окно Ханна (косинус – квадрат).
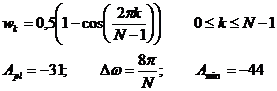
То есть прямоугольное окно минус косинуидальное окно.
Окно Хэмминга (приподнятый косинус).


Эти коэффициенты Хэмминг выбрал, чтобы наилучшим образом погасить боковые лепестки.
Оконное проектирование фильтров сводится к вычислению:

А потом преобразование её с умножением на коэффициент окна.

Метод аппроксимации частотных характеристик с помощью многочленов Чебышева.
Наиболее часто используемым подходом является метод, основанный на вычислениях многочленов Чебышева.
|
|
|

Такая аппроксимация частотных характеристик позволяет минимизировать абсолютное отклонение от желаемой кривой. Этот метод аппроксимации частотных характеристик используется и включён в пакет Matlab (remez).
Ремез Е. Я. – киевский математик, который разработал алгоритм для вычисления коэффициентов  .
.
При проектировании фильтров определяется уровень фильтрации и ширина переходной полосы.
Дата добавления: 2018-02-15; просмотров: 761; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
